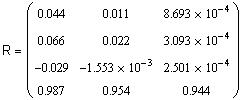
Рассмотрим функцию и исследуем ее многочлены Тейлора разногопорядка в окрестности точки (1,2)

Вычислим значение функции в данной точке

Вычислим частные производные и их значения в данной точке

Для вычисления частной производной щелкните символ дифференцирования в панели Calculus, введите переменную дифференцирования, символ функции или ее выражение, щелкните по стрелке в панели
Evaluation, затем вне выделяющей рамки.

Вычислим частные производные второго порядка и их значения в данной точке

Для вычисления частной производной второго порядка щелкните символ дифференцирования в панели Calculus, введите переменную дифференцирования, снова символ дифференцирования и необходимую переменную, символ функции или ее выражение, щелкните по стрелке в панели Evaluation, затем вне выделяющей рамки.

Теперь запишем многочлены Тейлора нулевого, первого и второго порядка для данной функции

Вычислим значения первых трех многочленов Тейлора, точные значения функции и остаточный член в трех точках, близких к точке (1,2): М1 (1.4,2.8), М2 (1.2,2.4), М3 (0.99,1.98)