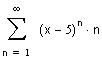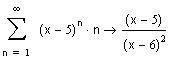
На границах области сходимости при х=4 и х=6 числовые ряды расходятся, так как не

выполняется необходимое условие сходимости: общий член ряда не стремится к нулю.

Поэтому область сходимости - интервал (4,6).Внутри этого интервала

Для того чтобы вычислить сумму рядя , щелкните по соответствующей позиции в панели Calculus, введите пределы суммирования и общий член ряда, нужный символ в панели Evaluation и щелкните вне выделяющей рамки

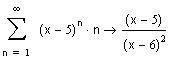
К сожалению, на левом конце области сходимости Mathcad не дает правильного ответа

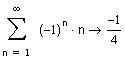
Посчитаем, например, частичные суммы и станет очевидно, что ряд расходится при х=4

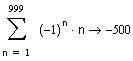
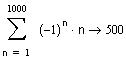
Лишний раз убеждаемся, что нет ничего практичнее, чем хорошая теория. Построим график суммы ряда

Для того чтобы построить график, щелкните по символу декартова графика в панели Graph и введите в помеченных позициях возле координатных осей имена аргумента и функции.

Для того чтобы изобразить на одном графике несколько функций одного и того же аргумента, введите в позиции возле оси ординат имя первой функции, введите запятую , имя следующей функции, запятую, и т.д., разделяя имена функций запятой.

Для того чтобы изменить стиль изображения, щелкните по графику дважды и измените параметры

изображения в открывшемся временном окне настройки изображения.

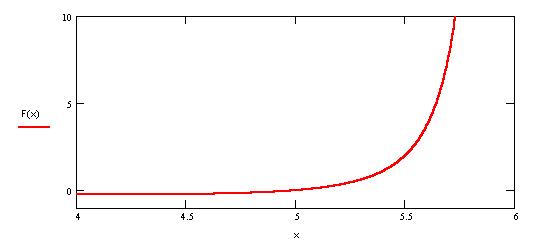
Важно понимать, что при любом х сколь угодно близком к х=4 внутри интервала сходимости функциональный ряд сходится к этой функции. Такой эффект связан

с понятием равномерной сходимости, с чем можно познакомиться в занятии 23.

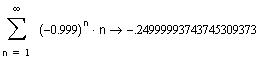
Рассмотрим функциональный ряд и вычислим его радиус сходимости

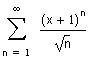
Исследуем сходимость ряда на границах интервала сходимости (-2,0)

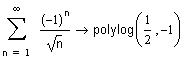
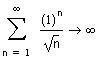
Не уточняя, чему равна сумма, заметим, что на левой границе интервала сходимости ряд

сходится условно и область сходимости - полуинтервал [-1,1).

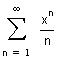
Рассмотрим ряд

Вычислим радиус сходимости этого функционального ряда

Для того чтобы вычислить предел , щелкните по соответствующей позиции в панели Calculus, введите функцию,

значение, к которому стремится n, нужный символ в панели Evaluation и щелкните вне выделяющей рамки

Исследуем сходимость ряда на границах интервала сходимости (-1,1)

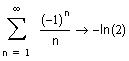
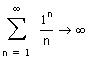
Для того чтобы вычислить сумму рядя , щелкните по соответствующей позиции в панели Calculus, введите пределы суммирования и общий член ряда, нужный символ в панели Evaluation и щелкните вне выделяющей рамки

Таким образом, область сходимости данного ряда представляет собой полуинтервал [-1,1).

В области сходимости ряд сходится к функции, которую можно вычислить средствами

Mathcad

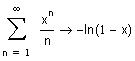
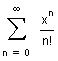
Рассмотрим ряд

Вычислим радиус сходимости этого функционального ряда

Область сходимости данного ряда - вся числовая ось. При любом х ряд сходится к функции

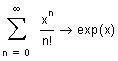
Рассмотрим функциональный ряд и вычислим его радиус сходимости