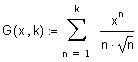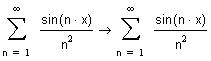
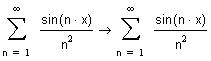
Рассмотрим ряд

Для того чтобы вычислить сумму рядя , щелкните по соответствующей позиции в панели Calculus, введите пределы суммирования и общий член ряда, нужный символ в панели Evaluation и щелкните вне выделяющей рамки

Так как члены данного рядя при любых значениях х не превосходят соответствующих

членов сходящегося ряда

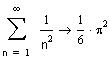
то по признаку Вейерштрасса рассматриваемый фуекциональный ряд сходится

равномерно на всей числовой оси. Сумма ряда символьно не вычисляется, поэтому

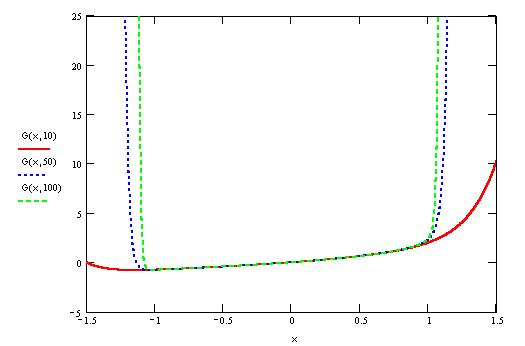
о пределим частичную сумму ряда и построим ее график.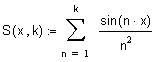

Для того чтобы построить график, щелкните по символу декартова графика в панели Graph и введите в помеченных позициях возле координатных осей имена аргумента и функции.

Для того чтобы изобразить на одном графике несколько функций одного и того же аргумента, введите в позиции возле оси ординат имя первой функции, введите запятую , имя следующей функции, запятую, и т.д., разделяя имена функций запятой.

Для того чтобы изменить стиль изображения, щелкните по графику дважды и измените параметры

изображения в открывшемся временном окне настройки изображения.

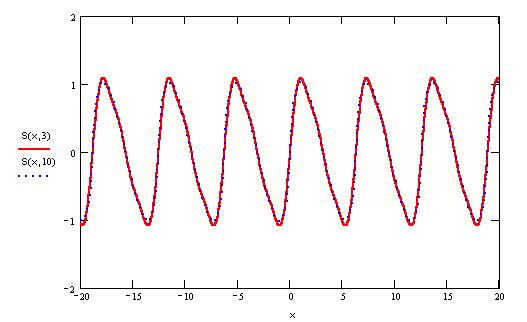
Рассмотрим ряд

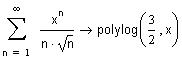
На отрезке [-1,1] члены рассматриваемого ряда по модулю не превосходят соответствующих членов сходящегося числового ряда

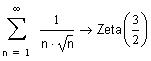
По признаку Вейерштрасса рассматриваемый фуекциональный ряд сходится

равномерно на отрезке [-1,1]. Сумма ряда выражается через незнакомые функции, поэтому о пределим частичную сумму ряда и построим ее график.