и может быть сделан как угодно малым при увеличении k. Следовательно на этом отрезке ряд сходится равномерно.

не превосходит

или после упрощения

На рассматриваемом отрезке остаток ряда

Для равномерной сходимости ряда нужно, чтобы начиная с некоторого номера остаток

ряда не превосходил заданного числа сразу для всех значений х. Как видно из графиков

остатка, на интервале (0,1) это невозможно. Поэтому на этом интервале данный ряд не сходится равномерно.

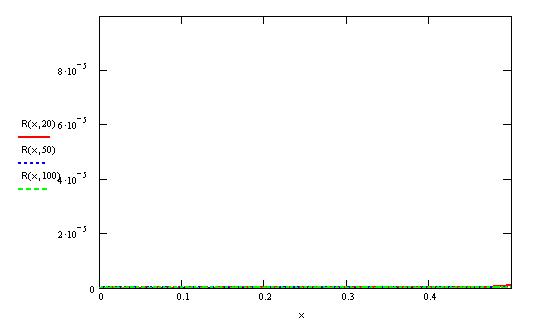
Рассмотрим тот же ряд на отрезке (0,0.5) и построим графики остатка ряда на этом

отрезке

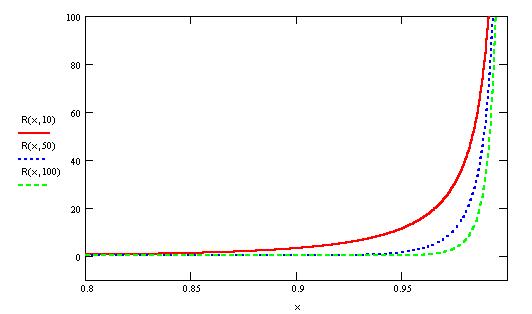
Поскольку поведение суммы ряда интересно вблизи х=1, график остаточного члена

построим на отрезке [0.8,1]

Для того чтобы построить график, щелкните по символу декартова графика в панели Graph и введите в помеченных позициях возле координатных осей имена аргумента и функции.

Для того чтобы изобразить на одном графике несколько функций одного и того же аргумента, введите в позиции возле оси ординат имя первой функции, введите запятую , имя следующей функции, запятую, и т.д., разделяя имена функций запятой.

Для того чтобы изменить стиль изображения, щелкните по графику дважды и измените параметры

изображения в открывшемся временном окне настройки изображения.

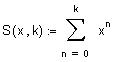
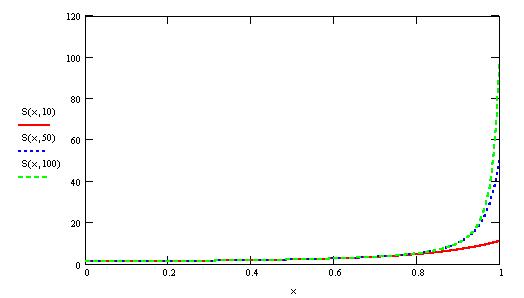
Определим частичную сумму ряда и построим ее график на отрезке [0,1], а также

график остатка ряда

Для того чтобы вычислить сумму рядя , щелкните по соответствующей позиции в панели Calculus, введите пределы суммирования и общий член ряда, нужный символ в панели Evaluation и щелкните вне выделяющей рамки

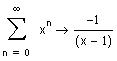
Рассмотрим ряд