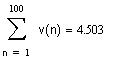
Так как ряд сходится, то частичная сумма приближенно равна сумме ряда. Точность

можно оценить, оценивая остаток ряда.

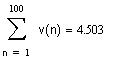
Исследуемый нами ряд ведет себя также, как и ряд из v3(n), который сходится. Вычислим частичную сумму ряда

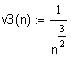
Для использования теорем сравнения наибольшую трудность представляет выбор ряда, с которым сравнивать. Можно попробовать разные ряды, если сразу не удается

понять поведение общего члена ряда при больших n.

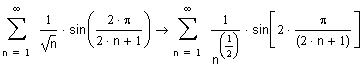
Рассмотрим ряд

Так как ряд сходится, то частичная сумма приближенно равна сумме ряда. Точность

можно оценить, оценивая остаток ряда.

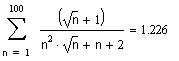
По второй теореме сравнения исследуемый ряд сходится. Вычислим частичную сумму

Для того чтобы вычислить предел , щелкните по соответствующей позиции в панели Calculus, введите функцию,

значение, к которому стремится n, нужный символ в панели Evaluation и щелкните вне выделяющей рамки

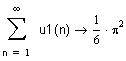
Сумма ряда символьно не вычисляется, поэтому исследуем ряд на сходимость

Для того чтобы вычислить сумму рядя , щелкните по соответствующей позиции в панели Calculus, введите пределы суммирования и общий член ряда, нужный символ в панели Evaluation и щелкните вне выделяющей рамки

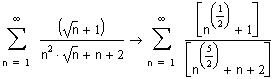
Рассмотрим ряд