Исследовать неоднородную систему для двух различных правых частей методом Гаусса.
Введем матрицу ![]() и столбцы правой части
и столбцы правой части ![]() и
и ![]() .
.
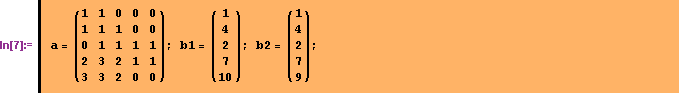
Загрузим пакет ![]() .
.
![]()
Сформируем расширенные матрицы системы ![]() и
и ![]() с помощью функции
AppendRows.
с помощью функции
AppendRows.
![]()

![]()

Приведем эти матрицы к ступенчатому виду с помощью функции RowReduce.
![]()

![]()

Видно, что система ![]() несовместна, а система
несовместна, а система ![]() совместна.
совместна.
Свободные переменные – ![]() . Решим эквивалентную
систему.
. Решим эквивалентную
систему.
Запишем общее решение системы.


Если нужно найти только одно произвольное решение этой системы, можно воспользоваться функцией LinearSolve.
![]()

С помощью встроенной функции Solve можно
сразу найти все решения системы. Только сначала
нужно сформировать соответствующую систему
линейных уравнений. Для этого введем вектор
переменных ![]() и с помощью функции Apply сформируем систему
уравнений.
и с помощью функции Apply сформируем систему
уравнений.

![]()
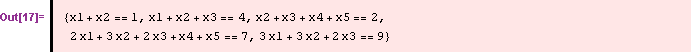
Теперь решим систему уравнений.
В данном случае выражение ![]() эквивалентно выражению
эквивалентно выражению ![]() .
.
![]()
![]()
![]()
Функция Solve выдала сообщение, что она не может разрешить эту систему относительно всех неизвестных переменных.
![]()