Вернуться на страницу <Методические разработки>
В начало

Занятие 11. Предел функции. Дифференцирование

• Вычисление пределов функций
• Дифференцирование
• Исследование функций

Три нижних кнопки инструментальной панели Calculus

предназначены для вычисления пределов функций.

Попробуем вначале вычислить замечательные пределы.

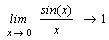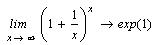
Как видно, получен вполне удовлетворительный результат.

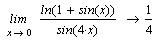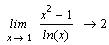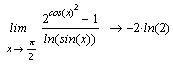
Можно вычислить также пределы слева и справа.

Так предел функции 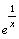при x -> -0 равен 0, а при x -> +0 - бесконечности.

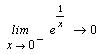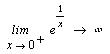
Вычисление предела - это операция символьной математики и поэтому завершается символом стрелки вправо
->.

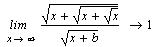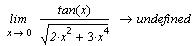
Дифференцирование

По определению, производная функции есть:

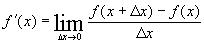
Вычислим по определению производную функци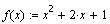и при :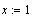

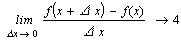
В Mathcad для вычисления производной используется палитра Calculus. Так, для решения той же задачи мы могли написать:

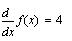
Причём символ дифференцирования выбирается только с палитры, вводить его "вручную" нельзя.

Заканчивается операция дифференцирования знаком =, если вы хотите получить численное значение производной в точке, и значком ->, если необходимо получить символьное значение.

Рассмотрим несколько примеров:

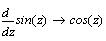
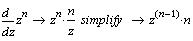
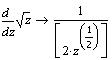
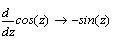
Поскольку переменная х определена, можно вычислить и довольно экзотическую производную

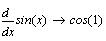
Исследование функций

Предел функции и производную можно использовать для исследования функций. Мы не будем рассматривать полную схему исследования, вычислим лишь точки экстремума и найдём наклонные асимптоты.

Рассмотрим функцию

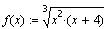
на интервале .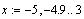

Вычислим производную:

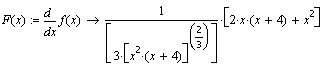
В точке локального максимума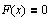

Разрешим это уравнение

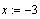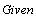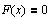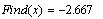
Наклонная асимптота определяется уравнением:

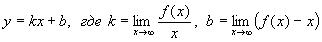
Вычислим

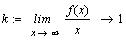
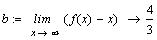
и построим на том же графике асимптоту.

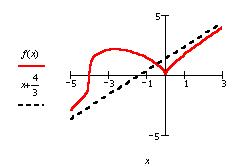
Можно ещё вычислить предел производной в точке х=0 слева и справа.

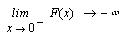
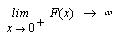
В нуле функция непрерывна, но производная имеет разрыв второго рода.

Рассмотрим ещё одну задачу. Необходимо построить эллипс

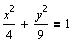
касательные и нормали к нему в точках
( ), ( ).

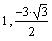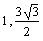Для простоты запишем уравнение эллипса в параметрической форме:

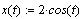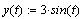
Положим 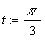, для точки 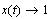, 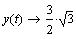и вычислим угловой коэффициент касательной.

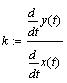
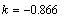   - свободный член уравнения

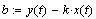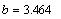
Угловой коэффициент нормали вычисляется как 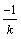  и свободный член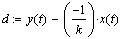

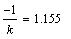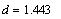
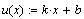- касательная

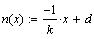-нормаль

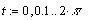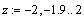
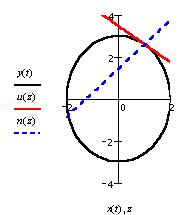
Нормаль и касательную в т. (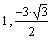 ) постройте самостоятельно.

Задание для самостоятельной работы

Построить графики функций:

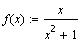
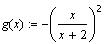
Найти:

1. Нули функций.
2. Точки локальных экстремумов.

В начало
Вернуться на страницу <Методические разработки>