Вернуться
на страницу <Методические разработки>
В начало
Занятие 10. Интерполяция функций
Нередко возникает необходимость
интерполяции функций заданных таблично. Для
простоты рассмотрим таблицу значений функции с
постоянным шагом. Пусть функция задана таблицей,
где первый столбец, х-координата, а второй,
y-координата.

Построим график
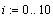
Для простоты считаем, что значения аргумента
функции упорядочены по возрастанию.
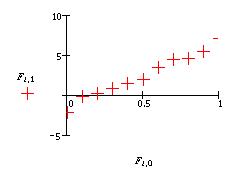
Допустим, нам необходимо вычислить значение
функции в точке x=0.53. Очевидно, необходимо
построить уравнение прямой проходящей через две
ближайшие точки 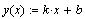 и вычислить значение функции для данного
значения аргумента. Это линейное приближение. и вычислить значение функции для данного
значения аргумента. Это линейное приближение.
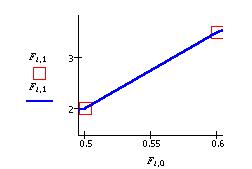
Уравнение прямой проходящей через две точки:
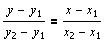
Напишем программу линейной интерполяции.
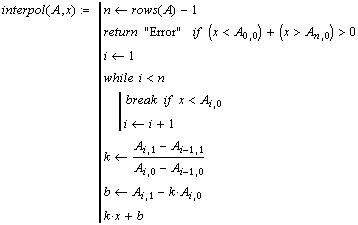 |
- количество строк матрицы - 1 |
| - лежит ли х в диапазоне? |
| - вычисляем индекс точки справа |
| - угловой коэффициент |
| - свободный член уравнения |
| - возвращаемое значение |
Теперь можно вычислить значение при х = 0.53:
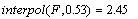
Задание для самостоятельной работы
По аналогии с рассмотренной программой
напишите программу квадратичной интерполяции.
Указание: Для вычисления
значения функции в этом случае необходимо
построить параболу по трём соседним точкам.
В Mathcad реализованы стандартные
функции для линейной интерполяции linterp() и функция interp() для кубической
сплайн-интерполяции.
1. Линейная интерполяция
Функция 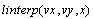 : :
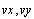 - векторы
данных упорядоченные по возрастанию; - векторы
данных упорядоченные по возрастанию;
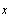 - аргумент,
для которого возвращается вычисленное значение. - аргумент,
для которого возвращается вычисленное значение.
Для нашего случая:
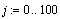 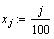 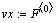 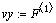
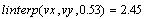
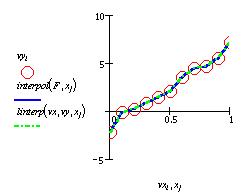
Построим на графике обе эти зависимости и
исходный набор точек:
Примечание: Операция 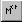 вырезает столбец
двумерной матрицы. вырезает столбец
двумерной матрицы.
2. Кубическая
сплайн-интерполяция
Кубическая сплайн-интерполяция позволяет
провести через набор точек гладкую кривую так,
чтобы в этих точках были непрерывны первая и
вторая производные. Вначале вычисляется вектор
вторых производных для чего имеется набор из 3-х
функций:
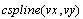 -
генерирует кривую, являющуюся кубическим
полиномом в граничных точках; -
генерирует кривую, являющуюся кубическим
полиномом в граничных точках;
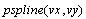 -
соответственно, параболу; -
соответственно, параболу;
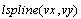 - прямую. - прямую.
Вычислим:
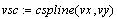 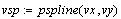 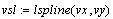
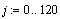 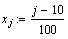
Построим график для всех 3-х вариантов.
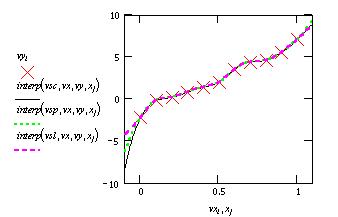
Мы специально сместили график на 0.1 в обе
стороны, чтобы увидеть разницу в сглаживании на
границах интервала.
Задание для самостоятельной работы
Функция задана таблицей значений:
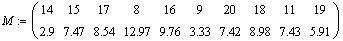
- Упорядочить массив данных по возрастанию
аргумента (1 строка).
- Построить график зависимости, сглаживая
сплайнами.
В начало
Вернуться на страницу
<Методические разработки> |

