Вернуться
на страницу <Методические разработки>
В начало
Занятие 9. Программирование. Численные методы
Система программирования в Mathcad
организована довольно хорошо, но к сожалению
абсолютно отсутствует возможность отладки, что
приводит к определённым трудностям в поисках
ошибки. Кстати, большинство ошибок связаны с
выходом индекса за пределы массива.
В качестве следующей задачи рассмотрим
простейший метод численного решения уравнений -
"метод половинного деления". Идею метода
рассмотрим на примере уравнения, аналитическое
решение которого в принципе невозможно.
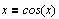
Преобразуем уравнение перенося всё за знак
равенства.
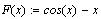
Рассмотрим полученную функцию. Очевидно,
решение задачи эквивалентно решению уравнения 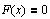
Построим график.
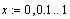
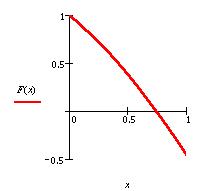
Решать задачу будем следующим образом:
- Зададим отрезок [a;b ] на
котором находится решение, например [0;1].
- Если выполнено условие
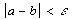 закончить работу и вернуть
результат, иначе: закончить работу и вернуть
результат, иначе:
- Поделим отрезок пополам
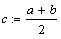
- Если функция F(x) сменила
знак на отрезке [a;c ], значит
там находится решение и мы определим новое
значение переменной b:=c ;
иначе a:=c.
- Вернёмся на пункт 2.
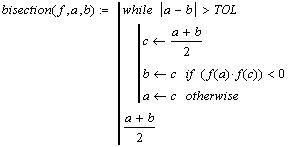
Здесь мы воспользовались системной переменной
TOL для задания точности вычислений и
использовали оператор цикла с предусловием while.
Для нашей задачи: 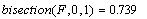
Программа имеет массу недостатков:
- Если решения на отрезке нет, то результат будет
недостоверен. Так, при неудачном задании
интервала, получим:
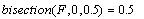
- Если решений на отрезке будет больше одного,
результат также не очевиден.
Более корректный алгоритм "метод Ньютона"
реализован во встроенной функции root().
Задание для самостоятельной работы
Составьте программу для нахождения корня
уравнения методом Ньютона.
Указание. Воспользуйтесь итерационной
формулой вычисления корня для уравнения f(x)=0 :
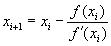
Вычисление бесконечных сумм
Рассмотрим формулу:
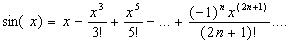
Для вычисления функции с заданной точностью e необходимо оборвать
суммирование когда очередное слагаемое станет
меньше e.
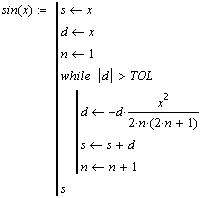
Здесь мы воспользуемся тем, что каждый
последующий член суммы выражается через
предыдущий
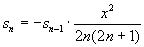 . .
Для проверки вычислим:
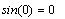 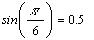 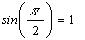
Задание для самостоятельной работы
Вычислить с заданной точностью 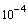 значение функции: значение функции:
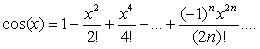 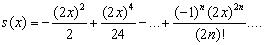 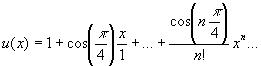 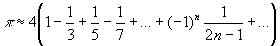 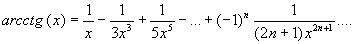 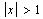
Приведём ещё программу перевода
десятичного числа в двоичное представление.
Здесь функция 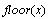 - ближайшее
целое меньшее - ближайшее
целое меньшее 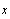 ., а ., а 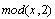 - остаток от
деления по модулю. - остаток от
деления по модулю.
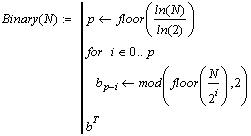
Например:
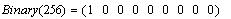
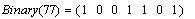
Примечание. 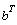 - транспонированная матрица, а не
степень - транспонированная матрица, а не
степень 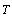 . .
В начало
Вернуться на страницу
<Методические разработки> |

