Вернуться
на страницу <Методические разработки>
В начало
Занятие 6. Встроенные функции
Mathcad имеет богатый набор встроенных функций.
Большинство из них просто возвращает значение,
однако имеются две функции, которые служат для
управления вычислениями.
1. Функция if(условие,оператор
1,оператор 2)
Если условие истинно,
выполняется оператор 1,
иначе оператор 2.
условие:
x=y Ctrl=
x>y
>
x<y
<
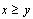 Ctrl 0 Ctrl 0
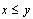 Ctrl 9 Ctrl 9
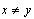 Ctrl 3 Ctrl 3
Результат логической
операции равен 0, если условие не выполнено, и 1,
если условие истинно. Этим свойством можно
пользоваться для создания более сложных
логических конструкций, например логическое
умножение:
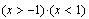 равно 1,
если истинны оба условия и 0 в противном случае . равно 1,
если истинны оба условия и 0 в противном случае .
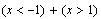 действует подобно логическому сложению.
действует подобно логическому сложению.
Используем, например, функцию if()
для корректного определения корней квадратного
уравнения:
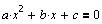 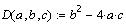

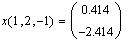 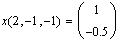
Используя свойства логических операций, можно
решить такую задачу:
пусть дано 1000 случайных чисел на интервале от 0 до
1. Требуется определить сколько чисел будет
больше 0.5.
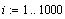 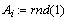 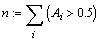 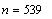
Функция rnd(n) возвращает
случайное число из диапазона [0; n].
Действительно, выражение в скобках равно 1, если
условие истинно, и 0 в противном случае. Мы
получим требуемое число.
Примечание. В Mathcad допустимы
двусторонние неравенства типа 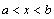 . .
Так, количество чисел попавших в диапазон [0.2;
0.5], будет 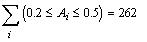 . .
Задание для самостоятельной работы
- Дана матрица размером 3*3 с произвольным набором
значений. Создать матрицу также размером 3*3, где
установить 1, если соответствующее значение
первой матрицы положительно, 0 - в противном
случае.
- Дан набор из 500 случайных чисел из диапазона от 0
до 8. Найти, сколько чисел попадёт на интервал от
3.2 до 4.7. Сравнить с тем, что должно получиться из
пропорциональности интервалов.
2. Функция until(x,z) возвращает
z пока х не становится
отрицательным.
Функция позволяет останавливать вычисления в
зависимости от условия и может быть полезна при
организации итерационной процедуры. Рассмотрим,
например, процедуру нахождения корней
трансцендентного уравнения методом Ньютона.
Для решения уравнения f(x)=0 итерационная
процедура реализуется формулой:
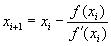
Рассмотрим решение уравнения x=cos(x),
считая, что решение найдено, если разность левой
и правой частей уравнения не превосходит
системной переменной TOL.
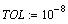 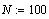 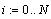 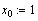 - начальное
значение - начальное
значение
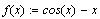
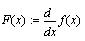 Знак
производной вводится с палитры Знак
производной вводится с палитры 
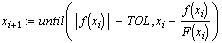 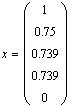
Как видно, для достижения заданной точности
потребовалось не 100 шагов, а всего лишь 3.
Обе эти функции позволяют достичь большей
гибкости вычислений, не прибегая к
программированию.
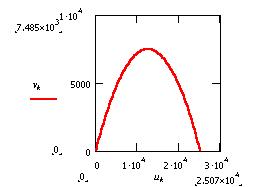
Задача о движении тела под углом к
горизонту
Уравнения движения: 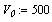 - начальная скорость, - начальная скорость, 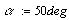 - начальный угол - начальный угол
Размерность угла в градусах вводится кнопкой Insert Unit.

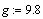 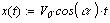 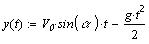 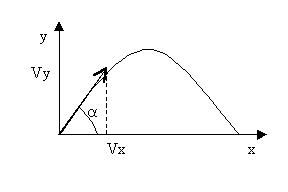
Проблема при построении графика возникает в
связи с тем, что мы не знаем заранее время
движения. Поэтому воспользуемся функцией until(...) при условии, что
y-координата должна быть неотрицательна.
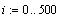 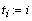 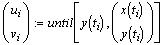 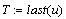 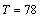 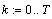
Т - время движения
округлённое до целого.
Нетрудно убедиться, что при изменении
начальной скорости и угла наклона вид графика
всегда остаётся неизменным. Нам пришлось только
задать интервал для i с
большим запасом до 500 с.
В начало
Вернуться на страницу
<Методические разработки> |

