Вернуться
на страницу <Методические разработки>
В начало
Занятие 4. Численные методы решения уравнений
1. Простейший способ найти
корень уравнения с одним неизвестным обеспечит
функция root() .
Например, нам необходимо найти корень
трансцендентного уравнения 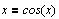 . Зададим
начальное значение . Зададим
начальное значение 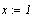 , решение дается функцией , решение дается функцией 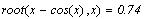 Точность вычислений
определяется системной переменной TOL равной по умолчанию Точность вычислений
определяется системной переменной TOL равной по умолчанию 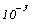 и определённой
в меню Math\Options .
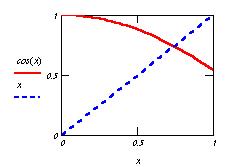
Проиллюстрируем полученное решение, определив
точность вычислений и определённой
в меню Math\Options .
Проиллюстрируем полученное решение, определив
точность вычислений 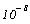 . .
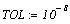 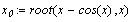 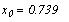 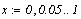
Здесь мы явно изменили значение системной
переменной TOL. 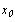 - переменная с текстовым индексом, который
вводится при помощи точки: x.0. - переменная с текстовым индексом, который
вводится при помощи точки: x.0.
Текстовый индекс - это просто декоративное
украшение, он является составной частью имени
переменной.
Отметим ещё, что при выводе результата
отображается только 3 значащих цифры после
десятичной точки. Эту установку можно изменить в
меню Format\Number в переменной Displayed Precision.
Две кривые строим, указав через запятую
cos(x), x.
2. Поиск корней при помощи
блока Given .........Find(...)
Обычно, перед тем как приступить к численному
решению, исследуют исходные уравнения с тем,
чтобы убедиться в существовании решения,
количестве корней, а также определения их грубых
приближений для задания начальной итерации.
Пусть задана система уравнений:
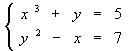
Нам нужно найти решение этой системы.
Выразим y как
функцию х и построим
график.
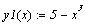 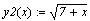 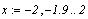
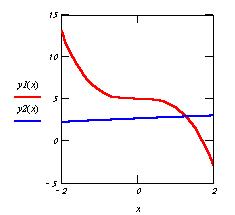
Нужно задать начальное приближение: 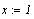 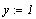
Далее вводим служебное слово
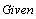
Затем описываем уравнения. Знак логического
равенства вводим Ctrl = или
выбираем из палитры инструментов.
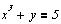
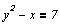
Решение даёт функция Find()
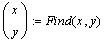 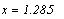 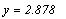
Здесь могут решаться системы уравнений с
несколькими неизвестными, однако, как и в
предыдущем случае, необходимо задание начальной
точки от которой будет происходить поиск
решения. Решение ищется методом итераций и при
наличии нескольких корней, очевидно, будет
найдено лишь ближайшее решение, если оно
существует.
3. Поиск решения при помощи
блока Given .........Minerr(...)
Практически то же, что и в предыдущем случае,
однако здесь численное значение будет найдено
даже при отсутствии решения. Дело в том, что здесь
ищется не решение уравнений а точка, где
достигается минимальное отклонение от искомого
решения. Рассмотрим функцию y(x)
и найдем точку, в которой эта функция наиболее
приближена к оси х.
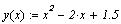 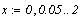
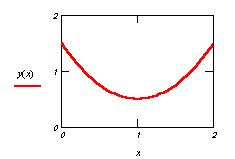
При построении графика необходимо явно указать
начальное значение на маркере оси y.
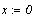 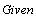 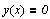
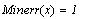
Первая строка даёт нам решение х=1, а системная
переменная ERR показывает невязку уравнения:
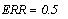
Аналогично решаются и более сложные уравнения
или их системы.
Примечание. Количество уравнений в
блоке Given .........Find(...) должно
совпадать с количеством неизвестных.
Задание для самостоятельной работы
Построить графическое решение уравнений и,
если решения имеются, найти численное значение.
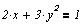
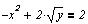 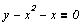
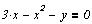 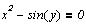
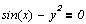 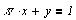
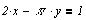
Решение систем линейных уравнений
Для решения систем линейных уравнений можно
использовать встроенную функцию lsolve(...) . Пусть задана
система линейных уравнений:
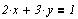
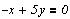
Матрицы коэффициентов:
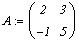 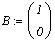
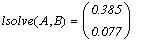
Эта же задача при помощи блока Given ... Find(...)
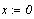 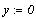 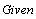 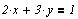 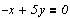 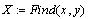
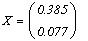
Примечание: Использование функции
lsolve() для решения систем линейных уравнений
является более корректным.
Задание для самостоятельной работы
Найти решение систем линейных уравнений:
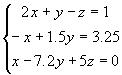
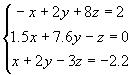 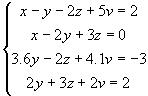
В начало
Вернуться на страницу
<Методические разработки> |

