Вернуться
на страницу <Методические разработки>
В начало
Занятие 2. Функции. Интервальная переменная
Определить функцию в Mathcad достаточно
просто, для этого необходимо ввести имя функции,
в скобках её параметры и оператор присваивания.
После чего вводится алгебраическое выражение.
Затем функция может использоваться наравне с
встроенными функциями. Введём для примера
параболическую функцию:
  
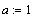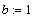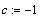
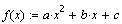
Нам пришлось предварительно описать три
константы a,b,c , иначе функция не может быть
вычислена.
Теперь, для того чтобы получить значение
функции, достаточно записать:
 
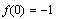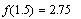
и так далее.
Однако, если бы этим ограничивались
возможности Mathcad, то этот пакет так бы и остался
большим калькулятором. К счастью, был
предусмотрен механизм многократного повторения
вычислений, нечто подобное циклам в языках
программирования. Введено понятие интервальной
переменной в формате:
:=начальное значение[,начальное
значение+шаг]..конечное значение
в скобках указан необязательный параметр шаг,
по умолчанию равный 1.
Двоеточие ".." вводится клавишей точка с
запятой"; " или кнопкой арифметической
палитры.
Введём для примера интервал изменения
аргумента x на отрезке [-2;2] с шагом h=0.1.
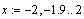
Фактически мы получаем набор из 41 значения
аргумента. Чтобы убедиться в этом, достаточно
ввести x=.
Для того, чтобы вывести таблицу значений
функции, введите f(x) и знак "=", вы
получите значения функции.
Таким образом можно увидеть только первые
50 значений.
Ну, а сейчас можно построить график.
Воспользуемся графической палитрой  , раскрыв
которую выберем x-y график.
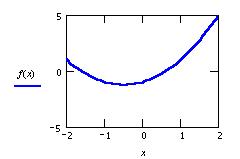
График строится довольно просто, нужно только
указать x переменную в маркере оси x и функцию f(x)
в маркере оси y. Заканчивается построение
клавишей Enter или щелчком мыши вне
графика.
Можно также явно указать начальное и конечное
значение по осям в маркерах начала и конца оси,
иначе они определятся автоматически. Выделив
график двойным щелчком мыши, можно произвести
его настройку, в частности, определить тип, цвет и
толшину линии, а также выбрать оси.
Есть ещё две интересные кнопки графической
палитры: 
Zoom - позволяет выделить часть графика,
Trace - отслеживает изменение координат на
графике.
Эти кнопки активны только при выделении графика.
Упражнение для самостоятельной работы
Постройте графики функций:
   
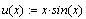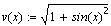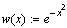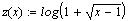
Диапазон для изменения аргумента по умолчанию
будет [-10; 10].
Матрицы и переменные с индексом
К сожалению, использование интервальной
переменной для построения функции вызывает
определённые трудности. Это связано с тем, что
при каждом обращении к интервальной переменной
система производит многократные вычисления и,
зачастую, совершенно напрасно пересчитывает
одни и те же значения. Чтобы избежать лишней
работы проще всего вычислить таблицу значений
функции один раз, а затем обращаться к табличным
значениям.
Для реализации данной задачи используется
интервальная переменная и переменная с индексом.
Например, если вернуться к предыдущей задаче,
можно решить её следующим образом:
- введём индекс, как интервальную переменную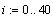 
- введём переменную с индексом, которая будет
меняться от -2 до 2 с шагом 0.1, для описания
переменной
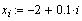
Если вычислить 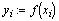 , мы получим вектор-столбец значений
функции.
Введите x= и y=, получите эти матрицы.
При помощи переменной с индексом мы создали две
одномерные матрицы с одним столбцом и 41 строкой.
Теперь можно вновь построить график, где в
качестве функции и аргумента мы и укажем эти
переменные с индексом.
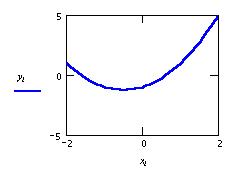
Примечание: на одном x-y графике можно
построить до 16 кривых. Функции вводятся через
запятую.
Аналогично можно использовать двумерную
матрицу для построения функции двух переменных,
например, определим функцию: 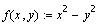 и две интервальных
переменных
 
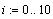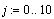
Теперь определяем две переменные с индексом:
 
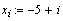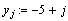
Определим двумерную матрицу: 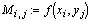 и построим
поверхность. 
В качестве единственного аргумента графика
указываем имя матрицы М
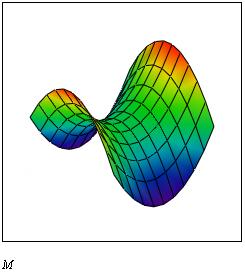
Для того, чтобы поверхность так выглядела
необходимо её настроить. Двойным щелчком мыши
вызываем меню настройки, устанавливаем опции
цвета, поворот 50 градусов и угол зрения 35.
В начало
Вернуться на страницу
<Методические разработки> |
