Вернуться
на страницу <Методические разработки>
В начало
Расчет разветвленных цепей постоянного тока
- Рассмотрим схему электрического моста, для
которой необходимо найти общее сопротивление R0.
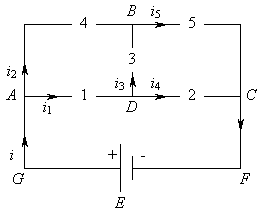 |
Запишем уравнения для узлов:
(В): 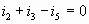
(D): 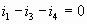
Запишем уравнения для контуров:
ACFG: 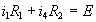
ABD: 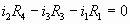
DBC: 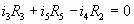 |
Задача сформулирована, имеется система из 5
уравнений с пятью неизвестными. Она имеет
единственное решение, т.к. 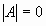 . .
Можно исключить переменные i5, i4
и прийти к стандартной системе трёх линейных
уравнений с тремя неизвестными, но эффективней
решать систему матричным способом с помощью
пакета математических программ MathCad.
Матричное уравнение: 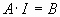
Составим матрицу из коэффициентов системы
линейных уравнений:
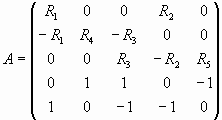 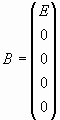
Матрица неизвестных токов: I = A-1·В [2].

а) Если все сопротивления 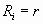 , то эта схема представляет
собой уравновешенный мост и , то эта схема представляет
собой уравновешенный мост и 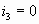 . .
Общее сопротивление моста в таком случае:
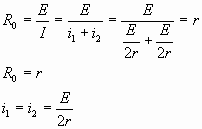
б) Если все сопротивления различны, то общее
сопротивление моста 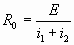 ,
где i1, i2 берутся из матрицы I. ,
где i1, i2 берутся из матрицы I.
Таким образом, задача решена в общем виде.
- Встречаются задачи, когда требуется определить
напряжение по тем или иным причинам, например, в
схеме, показанной на рисунке:
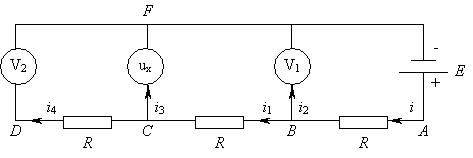
Запишем уравнения Кирхгофа:
Узел (В): 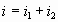 r
- внутреннее сопротивление вольтметра r
- внутреннее сопротивление вольтметра
Узел (С): 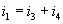 Е - источник э.д.с. Е - источник э.д.с.
Контур (ABF): 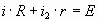
Контур (СDF): 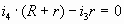
Контур (ВСF): 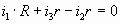
Исключим i из уравнения для контура (ABF) и
из уравнения для контура (ВСF).
Получим:
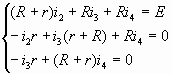
Решим полученную систему матричным методом: 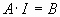 [2]. [2].
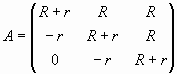 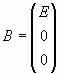 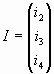 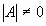
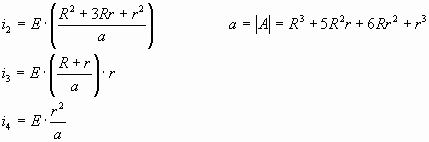
Так как 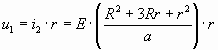 (1) (1)
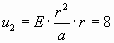 (2) (2)
Выразим Е из (2): 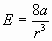 и подставим в уравнение (1).
и подставим в уравнение (1).
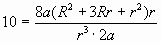
Обозначим через у выражение 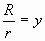 . .
Получим: 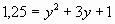 , или , или 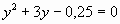
Решая уравнение, найдём у:
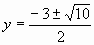
Поскольку отношение значений двух
сопротивлений не может быть числом
отрицательным, остаётся 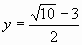 . .
Искомое напряжение 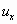 найдём по формуле
найдём по формуле 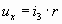 . .
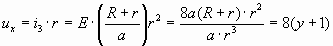
Подставим 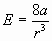 , получим: , получим:
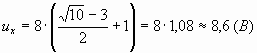
Таким образом, измерив напряжение в двух
доступных точках, можно определить напряжение в
недоступной точке.
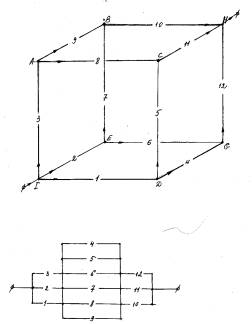
- Рассмотрим схему:
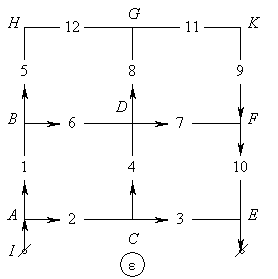 |
По второму закону Кирхгофа имеем:
BEG: 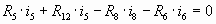 (1) (1)
DGKF: 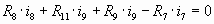 (2) (2)
ABDC: 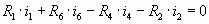 (3) (3)
CDFE: 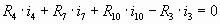 (4) (4)
Внешний контур: 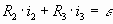 (5) (5)
|
Неизвестных токов 10, значит, должно быть 10
уравнений.
По первому закону Кирхгофа имеем:
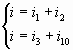
Узел В: 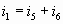 (6) (6)
Узел D: 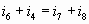 (7) (7)
Узел G: 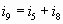 (8) (8)
Узел F: 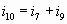 (9) (9)
Узел С: 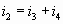 (10) (10)
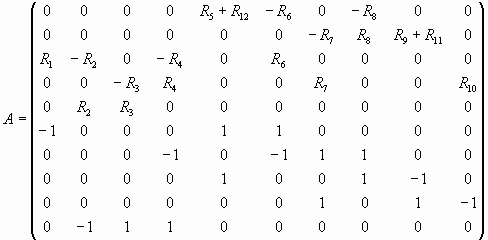  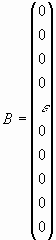
Задача решалась в системе MathCad [2].
Если все сопротивления 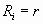 , то , то
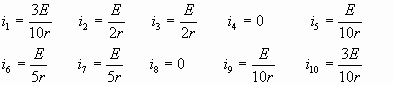
 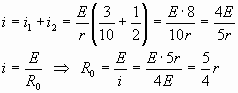
Используем второй закон Кирхгофа:
ACDI: 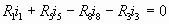 (1) (1)
ABEI: 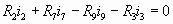 (2) (2)
BEGH: 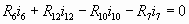 (3) (3)
ABHC: 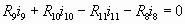 (4) (4)
СDGH: 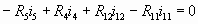 (5) (5)
IEGD: 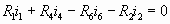 (6) (6)
Используем первый закон Кирхгофа:
Узел А: 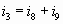 (7) Узел Е: (7) Узел Е: 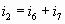 (11) (11)
Узел В: 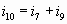 (8) Узел G: (8) Узел G: 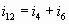 (12) (12)
Узел С: 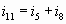 (9)
Узел H: (9)
Узел H: 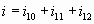 (13) (13)
Узел D: 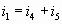 (10)
Узел I: (10)
Узел I: 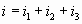 (14) (14)
Уравнения (13) и (14) используем для проверки
решения.
Всего получается 12 уравнений с 12 неизвестными,
но имеющаяся в наличии версия MathCad может работать
только с матрицами 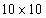 .
Поэтому i11 и i12 исключаем из
системы и получаем систему .
Поэтому i11 и i12 исключаем из
системы и получаем систему 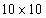 . .
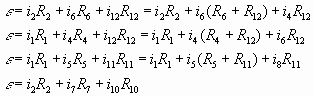
В общем случае (в символическом виде) система  не решается! не решается!
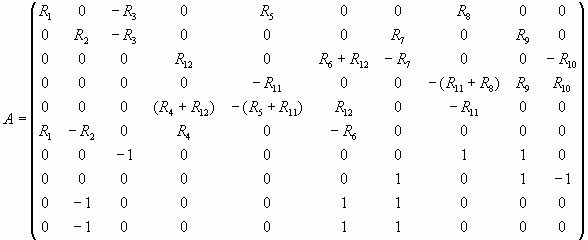  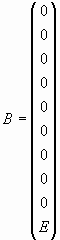
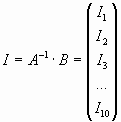 Задача решается
матричным методом в системе MathCad [2]. Задача решается
матричным методом в системе MathCad [2].
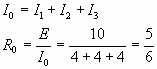
Ответ: 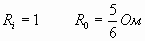
В начало
Далее |

