Вернуться
на страницу <Методические разработки>
В начало
Торможение атмосферой Земли падающих
космических тел
Постановка задачи
Одним из основных элементов строительных
конструкций является балка. Возьмём балку
(швеллер №40, последний из ряда, предлагаемого
ГОСТом таблиц сортамента) [5]. Определим
необходимую кинетическую энергию, необходимую
для того, чтобы балка потеряла прочность.
Рассмотрим схему, приведённую на рисунке.
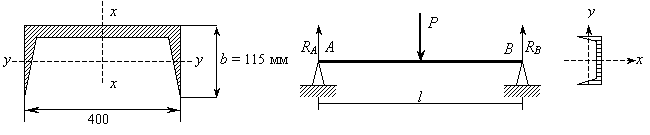
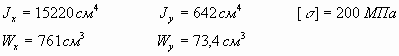
Будем считать, что прямое разрушение балки и
есть разрушение конструкции, или нарушение
герметичности сооружения.
Разрушение может наступить в случае, если
- превзойдён предел прочности металла, а именно
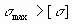 или или
- нарушена жёсткость балки, а именно прогиб балки
в месте приложения силы
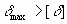 . .
Так, для консольной балки 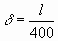 , для пролётов , для пролётов 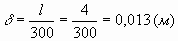 , где l - длина балки (положим l = 4м). , где l - длина балки (положим l = 4м).
Оценим максимально допустимую нагрузку на
балку. Проведём расчёт на прочность и жёсткость.
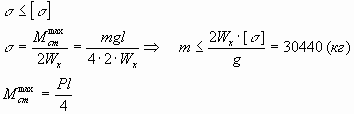 [3] [3]
где P - вес груза в центре балки (P = mg, g - ускорение
свободного падения), l = 4 м
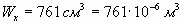 - момент
сопротивления сечения балки. - момент
сопротивления сечения балки.
Максимальный прогиб 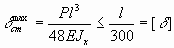
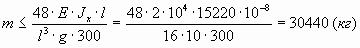
Вывод. Итак, максимальная масса, которую
может выдержать балка, 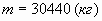
Если же груз падает со скоростью 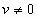 , то возникают
динамические напряжения, которые можно
рассчитать по формуле , то возникают
динамические напряжения, которые можно
рассчитать по формуле 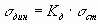 ,
где Кд - динамический коэффициент.
Тогда максимально допустимая масса уменьшается: ,
где Кд - динамический коэффициент.
Тогда максимально допустимая масса уменьшается:
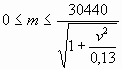
Если предположить, что падающее тело имеет
шарообразную форму, то можно оценить радиус шара
по формуле:
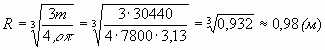 в случае, если в случае, если 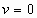 . .
Если же 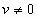 , то , то 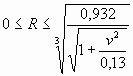
Графики зависимости 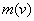 и
и 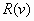 показывают, что с
увеличением скорости масса, необходимая для
разрушения балки, уменьшается. Так, при показывают, что с
увеличением скорости масса, необходимая для
разрушения балки, уменьшается. Так, при 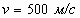 требуется
металлический шар радиусом 8 см и массой 20 кг. требуется
металлический шар радиусом 8 см и массой 20 кг.
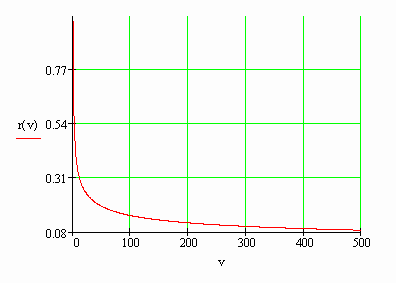
График зависимости радиуса космического тела
в виде шара от скорости падения на балку.
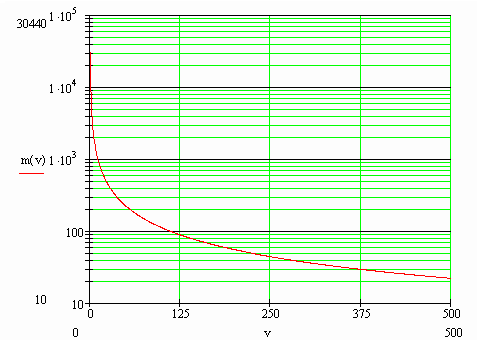
График зависимости массы космического
тела в виде шара от скорости падения на балку.
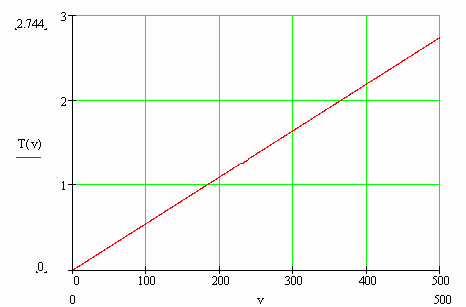
График зависимости предельной
кинетической энергии шара от скорости.
Кинетическая энергия шара под прямой
недостаточна для разрушения шара.
Процесс торможения падающих космических тел
атмосферой Земли настолько сложен, противоречив
и индивидуален, что требует для своего описания
решения системы нелинейных дифференциальных
уравнений в частных производных. При движении
космического тела в атмосфере скорость и масса
убывают. Это приводит к парадоксам. Например,
- кинетическая энергия в начальный момент
времени равна
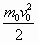 , ,
- кинетическая энергия тела через время
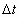 равна равна 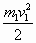 . .
Авторы [1, 79] утверждают, что "… метеорное тело
тормозится, нагревается, крошится, плавится и
испаряется. Но это только внешние признаки!
а) Предположим, что от космического тела
откололся кусок массой 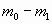 и летит он со скоростью и летит он со скоростью 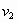 (крошится). Тогда в
соответствии с законом сохранения энергии (крошится). Тогда в
соответствии с законом сохранения энергии
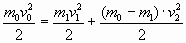
Запишем то же самое в несколько иной форме:
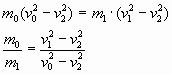
Получается, что 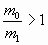 , а , а 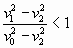 , чего не может быть! , чего не может быть!
б) Предположим, что кусок массой 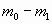 испарился, тогда
теплота парообразования r испарился, тогда
теплота парообразования r
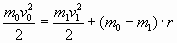 и и
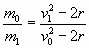
Получается, что 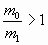 , а , а 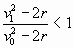 , чего также не может
быть! , чего также не может
быть!
Получается, что не так всё просто, как кажется
на первый взгляд.
Поэтому ограничимся рассмотрением частного
случая, достаточно хорошо изученного типа
движения.
Предположим, что космическое тело при входе в
земную атмосферу имеет нулевую скорость. И
начинает двигаться в атмосфере под действием
силы тяжести, тогда скорость будет изменяться
(переменная величина), а масса тела - нет
(постоянная величина). Уравнение движения можно
будет записать в виде
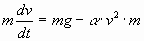 , где m - масса
тела, , где m - масса
тела,
v - скорость движения тела,
a - коэффициент сопротивления
воздуха.
Это дифференциальное уравнение первого
порядка с разделяющимися переменными.
Приведём его к виду, удобному для
интегрирования:
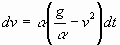
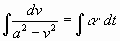 , где , где 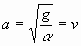 - скорость
парашютирования. - скорость
парашютирования.
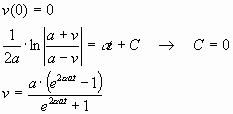
При 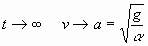 . .
Если 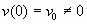 , тогда , тогда 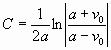
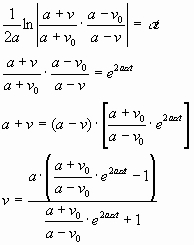
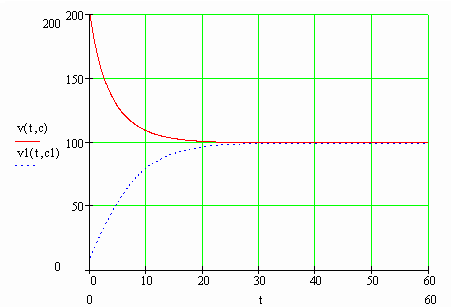
График зависимости скорости падения
шара от его начальной скорости.
Это известный факт, который проверен: если
начальная скорость тела больше или меньше а,
то через некоторое время из-за действия на тело
сопротивления воздуха скорость тела становится
равной скорости парашютирования. Плотность
воздуха меняется с высотой, что приводит к
зависимости плотности от высоты и коэффициента a. В данной работе берётся среднее и
постоянное значение параметра a.
Возьмём среднее значение 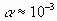 , тогда , тогда
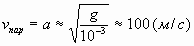
По расчётному графику найдём R(100) = 0,15 м, m(100)
= 109 кг.
Т.е. если на балку упадёт железный шар диаметром
30 см, то она выдержит, но если диаметр шара
будет больше 30 см, то она разрушится, что
может привести к аварийной ситуации.
В начало
Далее |

