Вернуться на страницу <Методические разработки>
Содержание

ОПЫТ ИСПОЛЬЗОВАНИЯ MATHCAD 6.0 PLUS И ELECTRONICS WORKBENCH 5.12 В ИНТЕГРИРОВАННОМ ПРОФОРИЕНТАЦИОННОМ КУРСЕ "ИНФОРМАЦИОННЫЕ И ЭЛЕКТРОННЫЕ ТЕХНОЛОГИИ" В СРЕДНЕЙ ОБЩЕОБРАЗОВАТЕЛЬНОЙ ШКОЛЕ № 1006 г. МОСКВЫ

Часть 2. Моделирование электрических цепей постоянного тока.

Приведем примеры использования MathCAD 6.0 PLUS и Electronics Workbench 5.12 для решения типовых задач, представляющих интерес для преподавателей информатики, математики, физики и технологии.

Рассмотрим тематическую цепочку "закон Ома для однородного участка электрической цепи" - "закон Ома для неоднородного участка - обобщенный закон Ома" - "правила Кирхгофа" , в которой пересекаются интересы физики, технологии и математики.

Создадим электронную модель однородного (резистивного) участка цепи в электронной лаборатории Electronics Workbench 5.12:

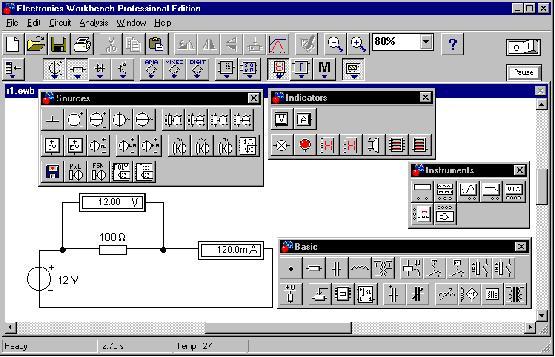
Параметры компонентов цепи (а также надписи-названия) редактируются в окнах, вызываемых двойным щелчком мыши по элементу схемы [2]. Использован источник постоянного напряжения (в европейском стандарте изображения), амперметр и вольтметр - в моде DC (Direct Current - постоянный ток).

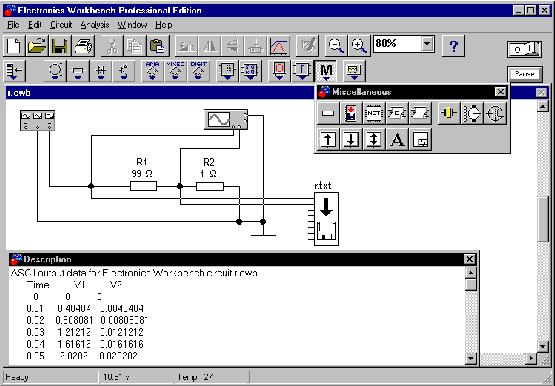
Воспользуемся функциональным генератором (Function Generator) для получения ВАХ резистора, подавая на резистор пилообразное напряжение. Длительность первого полупериода (Duty cycle) установлена на генераторе в 99% периода. Напряжение генератора подаем на канал A осциллографа (Oscilloscope) с резистора R1. Напряжение, прямо пропорциональное силе тока, подаем на канал B осциллографа с дополнительного резистора R2 по схеме характериографа:

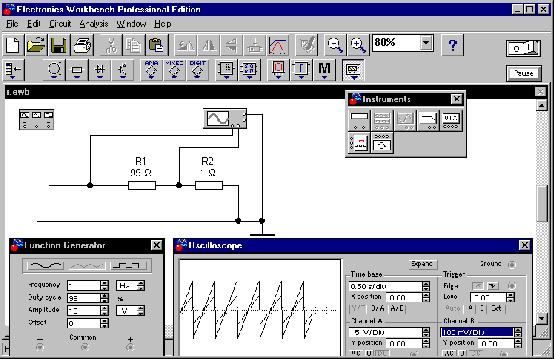
В режиме B/A осциллографа получаем фазовую диаграмму (экран прибора увеличен - кнопка "Expand"):

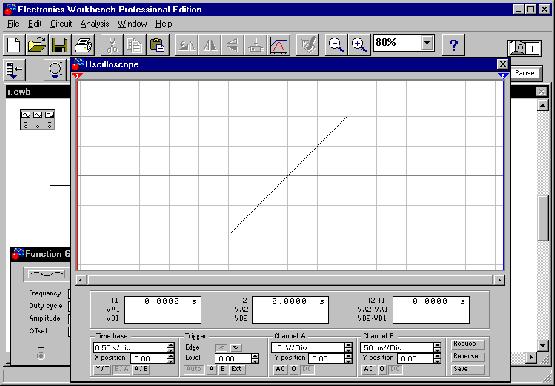
Cохранение диаграммы в графическом формате и её редактирование осуществляется в окне аналитических графиков (Analysis Graphs):

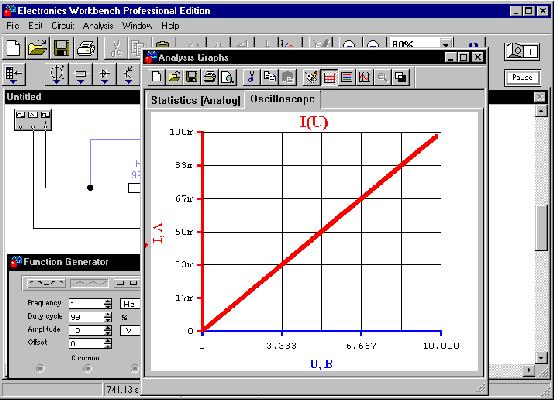
Для установки параметров осей, графиков и линий сетки щелчком правой кнопки мыши вызываем контекстные меню, где открываем окно "Свойства" ("Properties").

Математическая модель в MathCAD 6.0 PLUS дает график прямо пропорциональной зависимости. На втором графике ток и напряжение на резисторе заданы параметрически. Эта форма предпочтительнее для получения ВАХ электрических цепей синусоидального тока:

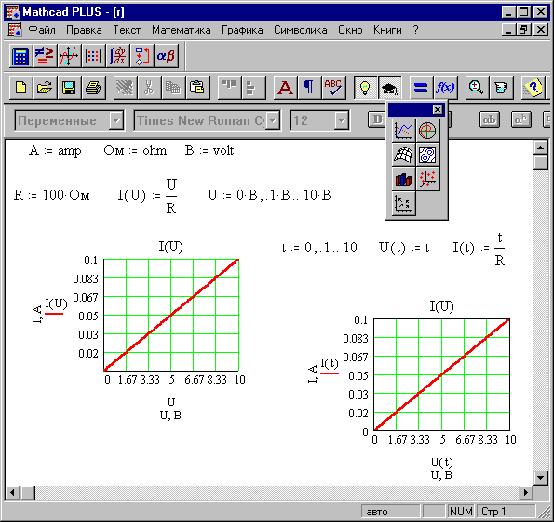
Как видим в начале документа, "русские" размерности физических величин легко определяются через встроенные переменные "английских" размерностей.

Устройство записи данных (Write Data) позволяет сохранить в текстовый файл уровни потенциала в 8 точках измерения. Данные импортируются в MathCAD как матрица (встроенная функция READPRN [1]) для дальнейшей численной или графической обработки, их можно также вставить в в окно "Описание" ("Description") документа электронной лаборатории:

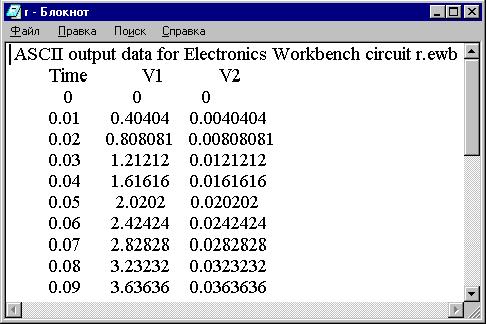
В MathCAD по оси абсцисс фазовой диаграммы выведены элементы второго столбца (номер столбца j = 1, - по умолчанию столбцы и строки массивов нумеруются, начиная с 0), а по оси ординат - третьего столбца:

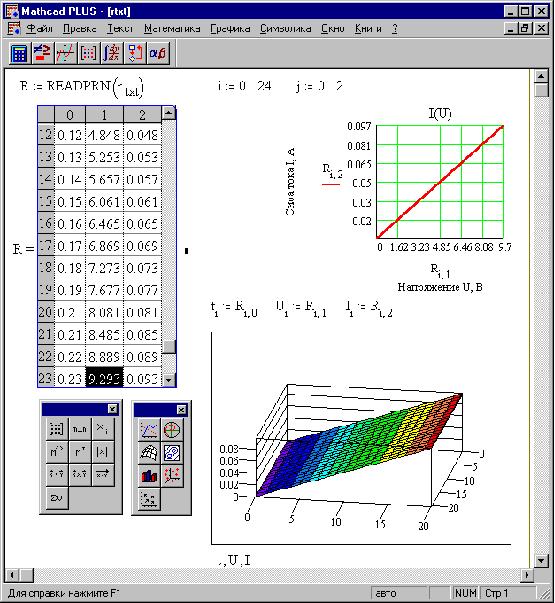
При создании графика поверхности ("пространства эксперимента") номер строки i использован как "естественный параметр". В окне также показаны палитры матричных операций и графиков, раскрытые щелчком левой кнопки мыши по панели символов (ниже меню).

Разумеется, в электронной лаборатории можно имитировать и "ручной" режим проведения опыта: увеличивать напряжение на резисторе, уменьшая сопротивление переменного резистора нажатием на клавишу [R] (или любую, назначенную пользователем) согласно определенному декременту. Показания приборов просто вводятся с клавиатуры в окно "Description" как в стандартном приложении Windows "Блокнот". Скопируем вид такого эксперимента:

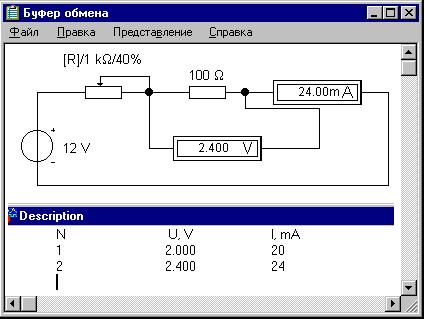
Копирование любой области окна Electronics Workbench 5.12 - команда "Копировать как точечный рисунок" ("Copy as Bitmap"), просмотр содержимого буфера обмена - команда "Показать буфер обмена" ("Show Clipboard") в меню "Правка" ("Edit").

Рассмотрим теперь модели неоднородных участков электрической цепи постоянного тока . На приборах, включенных с учетом полярности, в моде DC, отрицательные показания означают, что "минус" прибора (жирная черная черта) подключена более высокому потенциалу, чем "плюс" (тонкая черта), "против тока". Найдя направление тока в цепи, легко увидеть правило [3], согласно которому напряжение на резисторе записывается с "+" при совпадении направления обхода с направлением тока через резистор и с "-" в противном случае. Точно так же, значение включенной в участок ЭДС записывается с "+" при совпадении направления обхода с направлением действия сторонних сил - в направлении повышения потенциала и с "-" в противном случае:

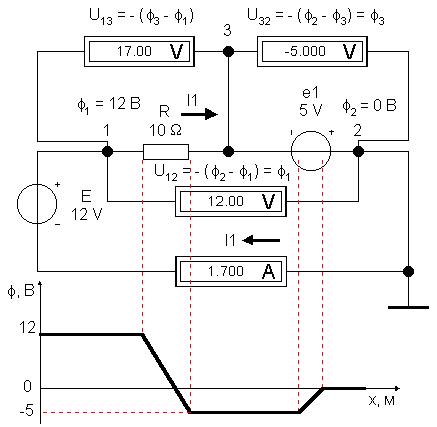
Как видим, при обходе неоднородного участка от узла 1 к узлу 2 падение напряжения на резисторе равно разности потенциалов узлов 1 и 2 плюс ЭДС:

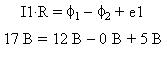
Аналогично, при обратном включении ЭДС (как на рисунке ниже):

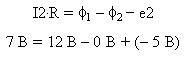
В обоих случаях резистор проходится в направлении тока, как это видно по показаниям приборов. Следует также учесть, что по умолчанию сопротивление амперметра в электронной модели равно 1 мОм, а вольтметра - 1 МОм.

Рисунки выполнены в приложении Visio Express for MathCAD, - в нем очень удобно создавать графические объекты как в MathCAD, так и в приложениях Microsoft Office.

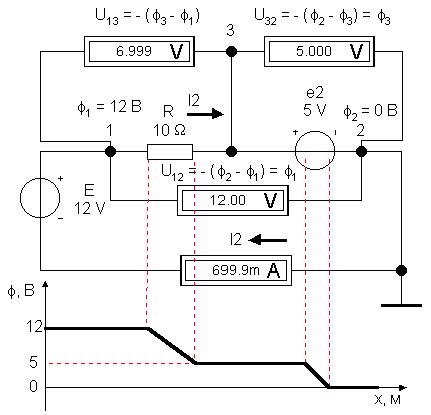
Объединение участков в контур и включение контура во внешнюю цепь на модели наглядно показывает выполнение правил Кирхгофа :

1. алгебраическая сумма токов в любом узле равна нулю;
2. при круговом обходе любого контура алгебраическая сумма падений напряжений на резисторах равна алгебраической сумме ЭДС.

Первое правило есть следствие закона сохранения электрического заряда ("в пересчете на 1 с") в форме уравнения напрерывности тока, второе - следствие закона сохранения энергии ("в пересчете на +1 Кл") с учетом потенциальности электрического поля цепей постоянного тока.

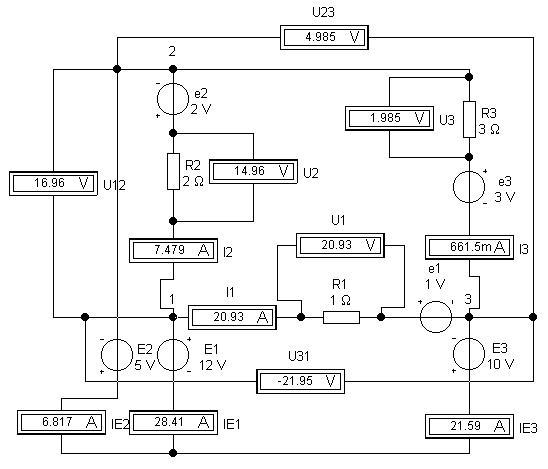
Например, как это видно по показаниям амперметров, в узел 1 "входит" ток IE1 = 28.41 А, а из узла "выходят" токи I1 = 20.93 А и I2 = 7.469 А:

IE1 - I1 - I2 = 0

При круговом обходе составленного из неоднородных участков контура по часовой стрелке (узел 1узел 2узел 3узел 1) сопротивления R2 и R3 проходятся "по току", а резистор R1 - "против тока"; ЭДС e1 проходится в направлении повышения потенциала, а ЭДС e2 и e3 - в направлении понижения потенциала:

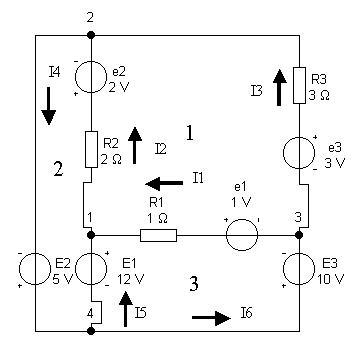
Освободив рассмотренную модель от измерительных приборов, запишем для полученной схемы систему линейных уравнений, обходя контуры по часовой стрелке, и решим её в MathCAD [3; 4; 5].

Направим произвольным образом токи в ветвях: I1 из узла 3 в узел 1; I2 из узла 1 в узел 2; I3 из узла 3 в узел 2; I4 из узла 2 в узел 4; I5 из узла 4 в узел 1; I6 из узла 4 в узел 3. В случае неправильно "угаданных" направлений соответствующие решения системы линейных относительно неизвестных токов уравнений получатся отрицательными.

Запишем первое правило Кирхгофа для узлов 1 - 3:

I1 - I2 + I5 = 0
I2 + I3 - I4 = 0
- I1 - I3 + I6 = 0

Для контуров 1 - 3 запишем второе правило Кирхгофа:

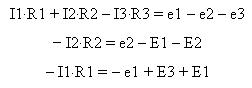
Перепишем систему уравнений в стандартной форме с учетом коэффициентов всех переменных и, определив в MathCAD матрицу коэффициентов при неизвестных A и вектор-столбец свободных членов b, применим встроенную функцию решения системы линейных уравнений LSOLVE(A,b) [1]:

Стрелки токов I1, I3 и I6 на рассмотренной схеме следует развернуть.

На практике десятиклассники, получив в MathCAD решение системы и значения определителей для применения правил Крамера, находят значения определителей "вручную" методом разложения по элементам строки или столбца. Сам этот метод легко обнаруживается, в том числе с помощью символьного процессора (аналитические преобразования математических выражений [1]) MathCAD, как это показано в учебном пособии [5], размещенном также на сервере фирмы Софтлайн (http://www.softline.ru).

Вообще, доступность результатов применения высшей математики в MathCAD "провоцирует" потребность разъяснить смысл её основных понятий, ориентируясь на физические и геометрические аналогии в представлении детей. При этом самым благодарным путем оказывается обращение к классике математики - к Ньютону, например: "Площадь кривой есть непрестанно рождающееся количество, увеличивающееся непрерывной флюксией (производной, - И.Х.), пропорциональной ординате кривой" (Исаак Ньютон. Математические начала натуральной философии (1687 г.)). Здесь функция предстает триединым процессом движения вправо по оси абсцисс [6]: за её ординатой, "управляемой" производной, нарастает площадь, формула изменения которой - неопределенный интеграл - и есть некий "итог" нарастания. "Разность итогов" - теорема Ньютона-Лейбница - очевидна для десятиклассника. Лошадь, всадник и путь - вот как ассоциируется живое понятие функции, и эта аналогия детьми принимается с удовольствием, хотя сам подход вызвал как положительные, так и резко отрицательные оценки у математиков-профессионалов, преподавателей вузов. В любом случае, по виду графиков степенных и гармонических функций десятиклассники легко "угадывают" формулы их производных и неопределенных интегралов, так что любая задача с применением аппарата математического анализа обязательно решается до применения MathCAD "вручную" , - это принципиальный момент ("не очевидные" задачи в нашем курсе не рассматриваются). Далее, поскольку построение поверхностных графиков и создание декартовых графиков их сечений в MathCAD чрезвычайно просто, то не вызывает затруднений и нахождение частных производных, и понятие полного дифференциала.

Применение дифференцирования облегчает работу с основным законом электродинамики и его использованием в электротехнике. В этих же отраслях благодаря интегрированию облегчен расчет действующих значений переменных величин - средних квадратичных. Наконец, формула полного дифференциала относительно абсолютных погрешностей прямых измерений позволяет в MathCAD легко находить формулы абсолютной и относительной погрешностей косвенных измерений [6; 7]. Причем выявление влияния погрешности прямого измерения на итоговую погрешность вызывает у детей почти "детективный" интерес.

Рассмотрим, например, применение символьных (аналитических) преобразований в MathCAD для получения формул абсолютной и относительной погрешностей косвенного измерения удельного сопротивления материала тонкой проволоки [7]. Такой анализ предваряет работу с физическими моделями, позволяя заранее оценить методику измерений.

Согласно закону Ома и определению удельного сопротивления найдем расчетную формулу для косвенного измерения:

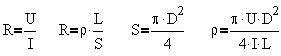
Определим формулу абсолютной погрешности косвенного измерения и, воспользовавшись "символьным равенством"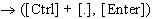, получим результат нахождения частных производных по прямо измеряемым переменным:

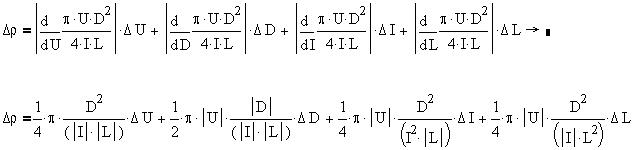
"Очистим" полученное выражение от скобок и значков модулей и определим формулу относительной погрешности косвенного измерения, которую упростим, выбрав команду "Разложить по степеням" из меню "Символика":

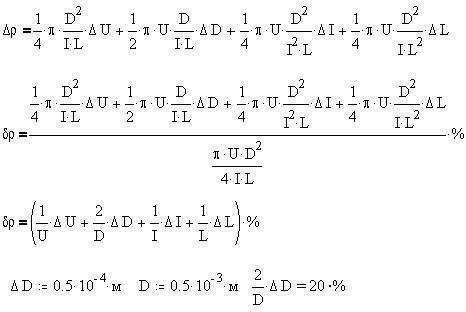
Измерение диаметра проволоки микрометром вместо штангенциркуля уменьшит вносимую погрешность на порядок.

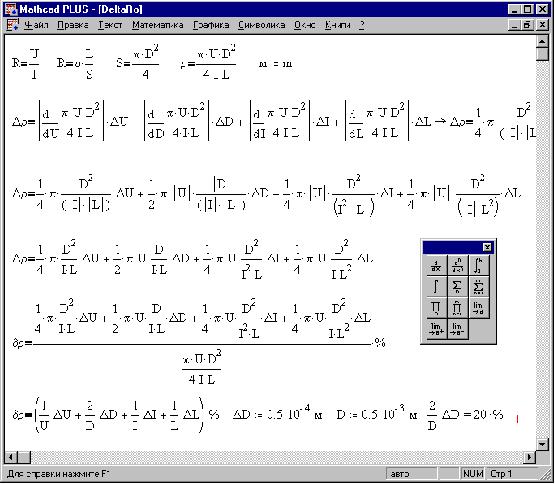
Ниже - окно MathCAD с рассмотренным документом и палитрой операций математического анализа:

Литература:

1. MATHCAD 6.0 PLUS. Финансовые, инженерные и научные расчеты в среде Windows 95./Перевод с англ. - М.: Информационно-издательский дом "Филинъ", 1996. - 712 с.
2. Electronics Workbench. Professional Edition. User's guide. Version 5./Interactive Image Technologies Ltd. Canada. 1996.
3. Иродов И.Е. Основные законы электромагнетизма: Учеб. пособие для студентов вузов. - 2-е, стереотип. - М.: Высш. шк., 1991. - 288 с.: ил.
4. Ходяков И.А. Основы электродинамики. Под ред. И.П. Дешко. Учебное пособие /МГДТДиЮ, МИРЭА - М., 1998, 47с.
5. Ходяков И.А. Элементы линейной алгебры. Под ред. И.П. Дешко. Учебное пособие /МГДТДиЮ, МИРЭА - М., 1998, 15с.
6. Ходяков И.А. Элементы математического анализа. Под ред. И.П. Дешко. Учебное пособие /МГДТДиЮ, МИРЭА - М., 1998, 16с.
7. Ходяков И.А. MATCAD 6.0. Практическое руководство для старшеклассников. Часть II. Под ред. И.П. Дешко. Учебное пособие /МГДТДиЮ, МИРЭА - М., 1998, 31с.

E-mail: sch1006@mtu-net.ru; sc1006@mirea.ac.ru
Телефон: 733-6727
Адрес: 119634, Москва, ул. Шолохова, 9

Содержание
Вернуться на страницу <Методические разработки>