Вернуться на страницу <Методические разработки>
Содержание

Творческий проект

ВЕКТОРЫ И МАТРИЦЫ В MATHCAD     Толстопятова Галина Порческу Оксана   10а класс

• Скалярное произведение векторов.
• Векторное произведение.
• Определитель матрицы.
• Слияние массивов.
• Расчет электрической цепи постоянного тока по правилам Кирхгофа.

В то время как обычные переменные (скаляры) хранят одиночное значение, массивы хранят много значений. Как обычно принято в линейной алгебре, массивы, имеющие только один столбец (строку), будут часто называться векторами, все прочие - матрицами. Одиночное число в Mathсad называется скаляром. Столбец чисел называется вектором, а прямоугольная таблица чисел - матрицей. Общий термин для вектора или матрицы - МАССИВ. Существует 3 способа создания массива :

1. Меню "Вставка" команда : "Матрицы"
2. Ctrl+ M
3. Панель инструментов.

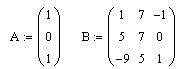
Арифметические действия между числами и массивами достаточно просты

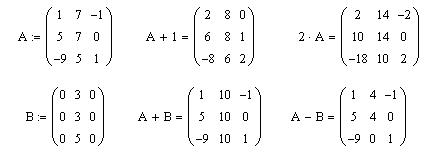
Операция совершается над каждым элементом Матрицы. Складываются или вычитаются элементы матриц с одинаковыми номерами строк и столбцов

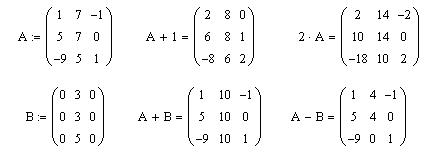
Умножение матриц более сложно. Приведем пример единичной матрицы, такой, что произведение матрицы А на единичную не меняет А.

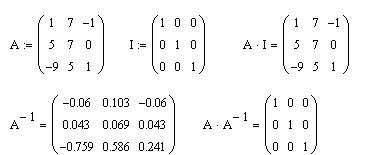
Матричная форма записи удобна для решения в Mathcad систем линейных уравнений.

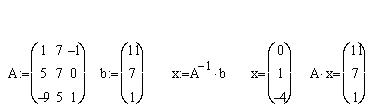
Скалярное произведение векторов.

Скалярное произведение векторов - произведение длин этих векторов на косинус угла между ними. Скалярное произведение векторов a и b будем обозначать символом ab. Если угол между векторами a и b равен f, то по определению скалярное произведение этих двух векторов выражается формулой: ab=|a|*|b|*cos f Аналогом в физике может служить работа А.

В данном случае F вектор силы, r - вектор перемещения, F*r - скалярное произведение. отсюда

Векторное произведение.

Векторным произведением вектора a на вектор b называется вектор c, обозначаемый символом с=[ab] и удовлетворяющий следующим трем требованиям: 1) Длина вектора с равна произведению длин векторов а и b на синус угла j между ними, т.е |c|=|[ab]|=|a|*|b|sin j 2) Вектор с ортогонален к каждому из векторов а и b 3) Вектор с направлен так, что тройка векторов аbc является правой. Вектор ,векторное произведение, составляет с векторами-множителями правовинто-вую тройку векторов, как, например, вектор напряженности поля силы Лоренца, равный векторному произведению вектора скорости движения точечного электрического заряда на вектор индукции магнитного поля:

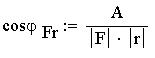
Пусть:

align="left">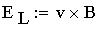

тогда:

align="left">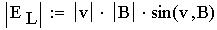

Чтобы не ошибаться в порядке сомножителей, можно воспользоваться следующим мне-моническим правилом: вектор х -это вектор-причина, которая всегда связана с измене-нием, движением(скорость движущегося заряда, например), вектор у -это вектор-обстоятельство в точке, где действует причина( например, электрическое поле на мгно-венной фотографии), вектор z- это вектор-результат действия причины в данных обстоя-тельствах(например, вектор индукции магнитного поля).Мнемоническим правилом можно воспользоваться при определении Силы Ампера, напряженности поля Силы Лоренца и линий магнитной индукции.

Определитель матрицы.

Определитель матрицы находится методом его разложения по элементам каких-либо строки или столбца. Если определитель матрицы имеет вид 3 х 3 ,то мы применяем к нему "правило диагоналей".

Слияние массивов.

Нельзя использовать команду Матрицы из меню Математика, чтобы создать массив, имею-щий более чем 100 элементов. Это ограничение применяется при создании нового массива или увеличении существующего. Можно, однако, создать большие массивы либо использованием функции augment,чтобы соединить массивы вместе, либо используя дискретный аргумент, либо считывая числа непосредственно из файла на диске.

1) использование функции augment

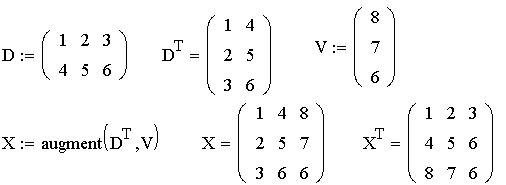
Использование дискретного аргумента:

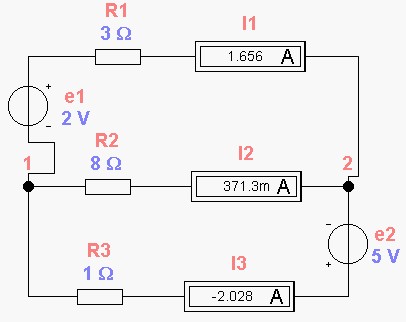
Расчет электрической цепи постоянного тока по правилам Кирхгофа.

Содержание
Вернуться на страницу <Методические разработки>