| Купить Matlab | Mathematica | Mathcad | Maple | Statistica | Другие пакеты | |
| Internet-класс | Примеры | Методики | Форум | Download | |

|
|
Системы компьютерной алгебры снабжаются специальным процессором для выполнения аналитических (символьных) вычислений. Его основой является ядро, хранящее всю совокупность формул и формульных преобразований, с помощью которых производятся аналитические вычисления. Чем больше этих формул в ядре, тем надежней работа символьного процессора и тем вероятнее, то поставленная задача будет решена, разумеется, если такое решение существует. Возможности символьного процессора представлены в меню "Символы". Открывая данное меню, мы видим множество элементов, которые можем использовать при вычислениях, но многие из них недоступны, не выделены цветом. Поэтому при работе с ними надо выделять переменную или выражение. Чтобы выделить выражение, нужно установить указатель мыши на переменную и с помощью клавиши пробел распространить синий уголок на все выражение. Команда "Символические" подменю "Расчеты" служит для обработки математических выражений, содержащих встроенные в систему функции, при этом выражение может быть представлено в различном виде: полиномиальном, дробно-рациональном, в виде сумм, произведений, производных, интегралов и т.д. Данная команда стремится произвести все возможные числовые вычисления и представить выражение в более простом виде. Для примера использования данной команды найдем интеграл от выражения
Сначала нужно ввести знак интеграла, потом ввести выражение, над которым будет производиться операция, потом пределы интегрирования и переменную интегрирования.
Теперь, установив курсор на выражении, нужно выбрать команду "Символические" подменю "Расчеты". Получим следующий ответ:
Ту же самую операцию можно проделать с помощью символьного знака равенства.
Данный интеграл мы искали при нахождении энергии магнитного поля. Найдем напряжение на конденсаторе. Оно пропорционально накопленному заряду.
Заряд изменяется как площадь под графиком зависимости силы тока от времени - как неопределенный интеграл от емкостного тока.
Подставим данные выражения в (1). В итоге напряжение равно:
Найдем действующее значение синусоидального тока, т. е. его среднее квадратичное:
Продифференцируем выражение x2 + 3x + 5. Введем оператор дифференцирования, дифференцируемую функцию, обязательно в скобках, выделим выражение и получим ответ:
Можно вычислить производную как первого, так и высшего порядка. Найдем производную второго порядка.
Те же самые операции можно производить с помощью комбинации клавиш Shift + F9. Найдем напряжение на индуктивности, оно равно работе электрического поля источника питания против ЭДС самоиндукции по переносу 1 Кл.
Команда "С плавающей точкой" подменю "Расчеты" заменяет константы, например p, в результатах символьных вычислений соответствующими числовыми значениями с заданным количеством знаков после запятой. Найдем интеграл от выражения C помощью команды "Символические" мы получим следующий ответ:
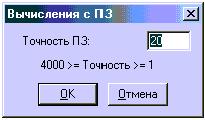
Если же мы будем использовать команду "С плавающей точкой", то получим конкретное числовое значение. Данная команда может дать ответ с 4000 верными цифрами. После выбора команды на экране появляется окно, в котором нужно указать количество знаков после запятой. Однако, если число знаков велико, система предлагает поместить результат вычислений в буфер обмена. Укажем 20 знаков.
Получим ответ: Если выбрать, например, 425 знаков после запятой, то Mathcad предложит поместить вычисления в буфер обмена. Появится диалоговое окно
На вопрос отвечаем "да", тогда ответ окажется в буфере обмена, выглядит это следующим образом:
Данную операцию можно произвести с помощью ключевого слова float, которое находится на панели "Математика, символьные операторы".
До слова float нужно ввести выражение, над которым будет производиться операция, а после запятой - количество знаков.
Команда "Комплексные" подменю "Расчеты" производит символьные вычисления и представляет результат в виде комплексного числа Re(z)+Im(z)i. Данное представление чисел широко применяется в электротехнике. Можно использовать данную команду для вычисления корней уравнения в том случае, если дискриминант меньше 0:
Также можно найти арифметический корень из отрицательного числа:
Команда "Упростить" упрощает данное выражение, открывает широкие возможности для упрощения сложных и плохо упорядоченных выражений, может также использоваться и для вычисления производных и интегралов. Если упрощение невозможно, то результатом будет исходное выражение.
Пример упрощения плохо упорядоченного выражения:
Однако нужно помнить, то вводить функцию нужно явно, т.е. нельзя задать функцию F(x), а потом искать ее производную или интеграл. Упрощать выражения можно, используя ключевое слово simplify. Следует открыть панель "Символы", щелкнуть по слову simplify, ввести упрощаемое выражение и нажать клавишу Enter.
Команда "Расширить" (точнее ее назвать "Разложить по степеням") противоположно команде "Упростить". Подвергаемое преобразованию выражение "расширяется" с использованием известных (а также введенных в символьное ядро) соотношений.
Данная операция производится только в том случае, если ответ однозначен. Например, сумма квадратов синуса и косинуса равна 1. Такое преобразование выполнимо.
Обратное преобразование многозначно, и поэтому в общем виде невыполнимо. Можно также использовать ключевое слово expand.
До слова expand нужно ввести выражение, а после запятой - условие преобразования, если же условие не имеет особой важности, то эту метку можно просто удалить:
Команда "Фактор" (точное ее название "Разложить выражение на множители") используется для факторизации - разложения выражения на множители или чисел на простые множители. Она способствует выявлению математической сущности выражения.
Вычисления с помощью ключевого слова factor:
Команда "Подобные" обеспечивает замену указанного выражения другим, скомплектованном по базису указанной переменной, если такое представление возможно.
Операция "Подобные" произведена по переменным a, b, c. Произведем данную операцию с помощью ключевого слова collect:
Если же такое представление невозможно, то система выдает сообщение об этом.
Команда "Коэффициенты полинома" служит для вычисления коэффициентов полинома. Команда применяется, если заданное выражение - полином (степенной многочлен) или может быть таким представлено относительно выделенной переменной. Подменю "Переменные" требует указания переменной, по отношению к которой выполняется операция. Для указания переменной достаточно установить на ней курсор ввода. Само выражение в данном случае выделять не надо, поскольку выделение в нем переменной является одновременно указателем на само выражение. Команда "Вычислить" подменю "Переменные" вычисляет значения указанной переменной, при которых данная функция равна 0. Это очень удобно при решении алгебраических уравнений, например квадратных и кубических, а также для вычисления корней полинома.
Если же уравнение не имеет корней, то значение переменной будет найдено в комплексном виде.
Команда "Замена" подменю "Переменная" подставляет новое выражение вместо указанной переменной. Выражение для подстановки должно быть предварительно скопировано в буфер обмена. В нашем примере таковым является выражение y-a, а исходным - x2 + x + 1.
Можно использовать ключевое слово substitute:
Наряду с получением результата в символьном виде эта команда позволяет найти и числовые значения функции некоторой переменной путем замены ее аргумента числовым значением. В этом случае в буфер обмена нужно поместить число для подстановки.
В подменю "Переменные" есть еще две команды: "Дифференциалы" и "Интеграция". С помощью этих команд можно дифференцировать и интегрировать выражение, содержащую выделенную переменную, по отношению к этой переменной. Найдем заряд как неопределенный интеграл от тока:
Найдем от этого же выражения производную:
Команда "Определитель" подменю "Матрицы" позволяет детерминант матрицы.
Воспользуемся возможностями символьного процессора для получения формул абсолютной и относительной погрешностей косвенных измерений на примере косвенного измерения удельного сопротивления материала тонкого провода. Согласно закону Ома и определению удельного сопротивления r проводника найдем расчетную формулу:
В формулу входят непосредственно измеряемые приборами физические величины: u - напряжение, i - сила тока, d - диаметр провода, l - длина провода. Пусть также известны абсолютные погрешности прямых измерений Du, Di,Dl, Dd. Для нахождения формулы абсолютной погрешности косвенного измерения можно использовать формулу полного дифференциала относительно конечных погрешностей прямых измерений:
Модули частных производных найдем с помощью символьных вычислений:
Теперь отредактируем формулу, получим:
Найдем более компактную формулу относительной погрешности как отношение выражения для абсолютной погрешности к выражению для удельного сопротивления:
Выделим правую часть равенства и применим к ней команду "Разложить по степеням":
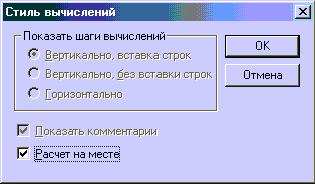
Как видим, относительная погрешность косвенного измерения определяется относительными погрешностями прямых измерений, причем процент ошибки измерения диаметра провода входит в формулу удвоенным. Последней командой является "Стиль вычислений". Она служит для установки стиля отображения выражений, над которыми выполняются символьные операции. При выборе данной команды появляется диалоговое окно, в котором нужно указать стиль вычислений. "Вертикально, вставка строк" обеспечивает вывод выражения под заданным с дополнительной вставкой строк, как и было во всех выше приведенных преобразованиях. "Вертикально, без вставки строк" выводит результат вычислений на место исходного выражения. "Горизонтально" обеспечивает вывод выражения рядом с исходным. "Показать комментарии" отображает комментарии по ходу вычислений.
"Расчет на месте" соответствует команде "Горизонтально", при этом все остальные команды становятся недоступными.
Также символьная система Mathcad позволяет решать системы уравнений с помощью команды Given - Find. Кинематика.Основные понятия, законы и формулы. 1. Механическим движением называют изменение взаимного расположения отдельных тел или различных частей одного тела, происходящее в пространстве с течением времени. В любом механическом движении всегда участвует не менее двух тел. Одно из них условно принимают за неподвижное тело отсчета и по отношению к нему определяют механическое состояние всех остальных тел. Чтобы установить законы механического движения тел относительно выбранного тела отсчёта, с ним связывают ту или иную систему координат - чаще всего прямоугольную и часы. Наиболее простой вид эти законы имеют в системах отсчета, связанных с поверхностью Земли, когда по условию задачи суточным и годовым вращением Земли можно пренебречь. Простейшим механическим движением является движение материальной точки - тела, размеры и форму которого можно не учитывать при описании его движения и массу которого можно считать сосредоточенной в точке. 2. Движение материальной точки характеризуют траекторией, длиной пути, перемещением, скоростью и ускорением. Траекторией называют линию в пространстве, описываемую точкой при своем движении. Длину дуги, отсчитываемою вдоль траектории от некоторой точки, принятой за начало отсчета, называют длиной пути (дуговой координатой). Перемещение - это вектор, соединяющий начальное положение движущейся точки и ее положение в рассматриваемый момент времени. 3. Положение материальной точки М на плоскости в прямоугольной - декартовой системе координат Оху определяют или заданием радиус-вектора , проведенного из начала координат в точку М, или двумя числами - координатами x, у точки М, представляющим собой проекции вектора на соответствующие оси. Если известна траектория точки М, ее положение в пространстве можно также определить заданием дуговой координаты s (длиной пути), отсчитываемой вдоль траектории от начала отсчета. При движении точки ее радиус-вектор и координаты изменяются и являются функциями времени:
4. Физическую величину, характеризующую
изменение положения точки в пространстве за
единицу времени, называют средней скоростью
перемещения. Если за время Dt точка переместилась
на
Средняя скорость перемещения--- величина векторная, ее направление всегда совпадает с направлением вектора перемещения. 5. Простейший вид механического движения--- прямолинейное движение точки с постоянным ускорением. Если ось координат направить в сторону начального смещения точки и за начало координат принять ее начальное положение, то для такого движения
Соотношения (1), (2), (5), выражающие законы изменения ускорения, скорости и перемещения с течением времени, называют соответственно уравнением ускорения, скорости и законом движения точки. Движение точки с постоянным ускорением включает в себя равномерное и равноускоренное. При равномерном движении скорость точки с
течением времени не меняется, и в уравнениях (2) и
(5) нужно положить 7. К равноускоренному движению можно отнести
движение тел под действием силы тяжести, если их
расстояние h по вертикали, отсчитанное от
поверхности Земли, мало по сравнению со средним
расстоянием тела до центра Земли. Так как сила
тяжести сообщает всем телам, находящимся на
одинаковом расстоянии от центра Земли,
одинаковое ускорение 8. Простейшим видом криволинейного движения является равномерное движение точки по окружности. При таком движении R = const, v = const. Если точка движется по окружности с радиусом R с линейной скоростью v, делая n оборотов за время t, то
соответственно число оборотов в единицу времени (скорость вращения) и продолжительность одного оборота (период обращения). 9. По характеру движения отдельных частиц твердого тела различают поступательное и вращательное движение тел. Кинематическими характеристиками вращательного движения тел служат угол поворота j, угловая скорость w и угловое ускорение a. Угловую скорость и угловое ускорение тел при вращении вокруг неподвижной оси можно определить аналогично скорости и ускорению прямолинейного движения:
Для тел, вращающихся с постоянным угловым ускорением, по аналогии с прямолинейным движением имеем:
В случае равномерного вращения w = const и в формулах (10) необходимо положить a=0. Из сравнения формул (7) и (9) видно, что линейная скорость v точек тела, удаленных от его оси вращения на расстояние R равна:
10. Очень часто движение тел рассматривают относительно какого-либо другого тела, которое в свою очередь перемещается по отношению к телу отсчета, принятому условно за неподвижное. Примеры решения задач.1. Средняя скорость движения. Дана задача. Велосипедист ехал из одного города в другой. Половину пути он проехал со скоростью v1 = 12 км/ч. Далее он ехал со скоростью v2 = 24 км/ч, а затем до конца пути шел пешком со скоростью v3 = 4 км/ч. Определите среднюю скорость велосипедиста на всем пути. Решение.
Составим уравнения движения для каждого отрезка пути и запишем дополнительные условия задачи:
Мы имеем 6 уравнений и 7 неизвестных (s1, s2, s3, t1, t2, t3, v). Если при решении задачи неизвестных получается больше числа уравнений, то при последующих вычислениях одно из них сократится. Подтвердим наше утверждение: (1),(2),(3)--(6):
Использование Mathcad. В данной задаче нам требуется найти только одну величину. Но если мы зададим только её, то Mathcad решения не найдёт, так как ему требуется задать для нахождения столько величин, сколько имеется уравнений. В данном случае требуется задать 6 величин. Теперь решим задачу, используя given - find:
А теперь выберем нужный нам ответ. 2. Рассмотрим задачу на относительность движения. Дана задача. От буксира, идущего против течения реки, оторвалась лодка. В тот момент, когда на буксире заметили лодку, она находилась от него на достаточно большом расстоянии s0. С буксира быстро спустили катер, который доплыл до лодки и возвратился с ней назад. Сколько времени заняла поездка катера, и какое расстояние он проплыл в одну и в другую сторону, если скорости катера и буксира относительно воды равны соответственно v1, v2? Решение. В задаче рассматривается равномерное движение тел относительно друг друга. В данном случае расчеты можно производить так, как если бы течения не было. Изучая относительное движение тел, систему отсчета удобно связывать с одним из этих тел. В предлагаемой задаче систему отсчета удобно связать с буксиром, так как все происходящие события рассматриваются по отношению к нему. В такой системе отсчета сам буксир покоится, лодка удаляется от него со скоростью v2, катер удаляется от буксира со скоростью v1 + v2, катер вместе с лодкой приближается к нему со скоростью v1 - v2. Обозначим время движения катера до лодки t1, а с лодкой обратно t2. Тогда уравнение движения для катера и лодки за время t1 s0+s1=(v1+v2)*t1, s1=v2*t1 а за время t2 s0 + s1 = (v1 - v2)*t2. Искомое время движения катера будет равно t = t1 + t2, а расстояние s = 2*(s0 + s1). Мы имеем 5 уравнений, содержащих 5 неизвестных (s1, t1, t2, s, t), из которых нам требуется s и t. Теперь запишем, что дано, и что требуется найти. Неизвестных надо записывать столько, сколько уравнений.
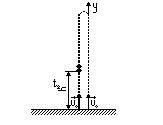
3. Движение тела, брошенного вертикально вверх. Дана задача. Тело брошено вертикально вверх с начальной скоростью v0=3.13 м/с. Когда оно достигло верхней точки полета, из того же начального пункта с такой же начальной скоростью бросили второе тело. Определите, на каком расстоянии h от точки бросания встретятся тела; сопротивление воздуха не учитывать. Решение. Для начала делаем чертеж.
Отмечаем на нем траекторию движения первого и второго тел, ось Oy направляем вертикально вверх. Записываем уравнения движения тел: для первого для второго Третье уравнение составляем с учетом того, что второе тело бросили позднее первого на время максимального подъема:
Запишем, что дано, и что требуется найти.
|
| | На первую страницу | Поиск | Купить Matlab | |
|
|

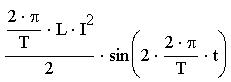
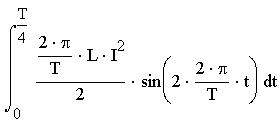
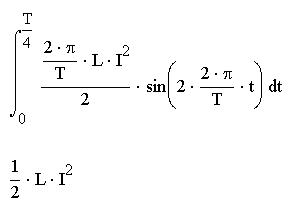
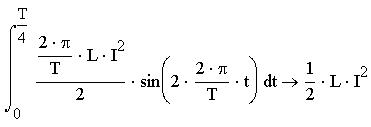
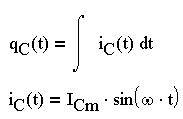
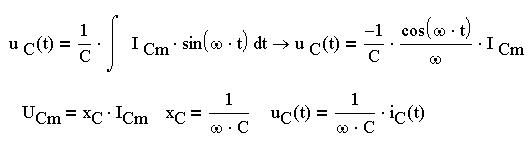
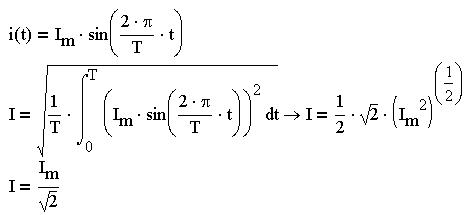
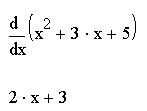
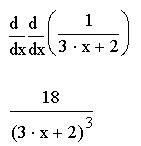
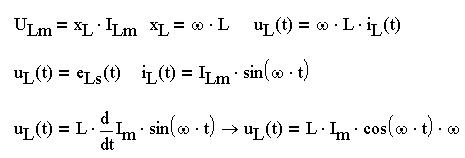
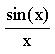
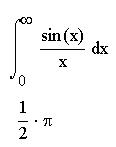
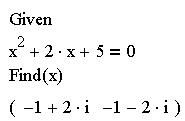
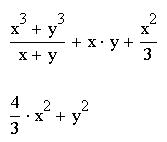
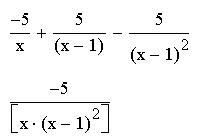
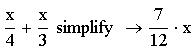
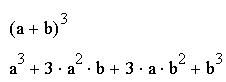
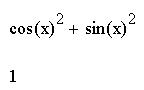
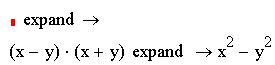
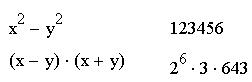
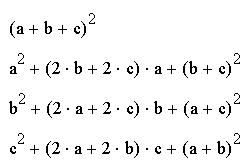
.jpg)
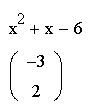
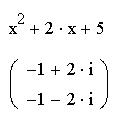
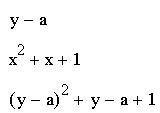
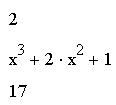
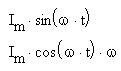
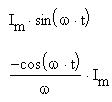
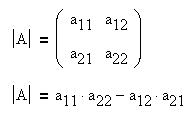
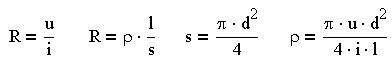
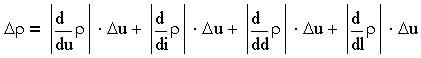
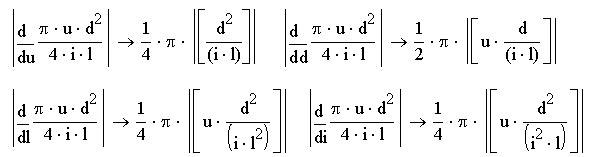
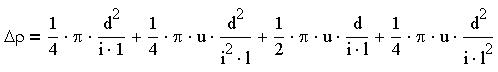
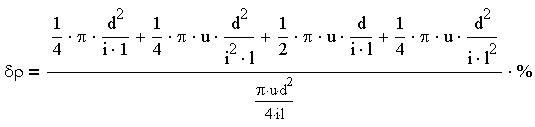
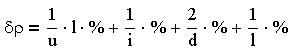
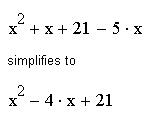
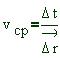
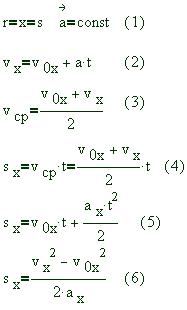
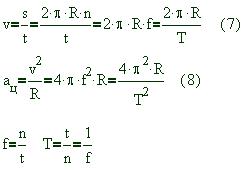
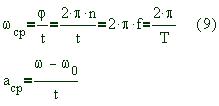
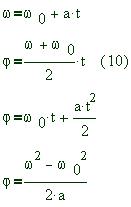
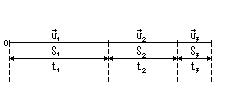
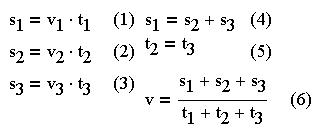
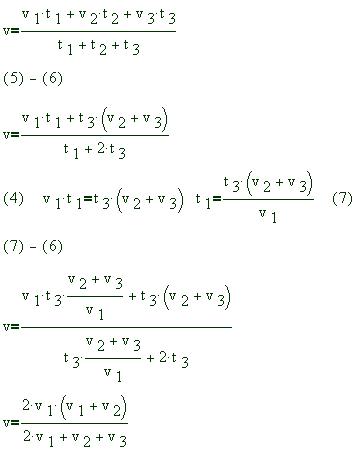


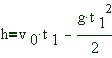
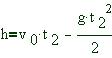 .
.