| Купить Matlab | Mathematica | Mathcad | Maple | Statistica | Другие пакеты | |
| Internet-класс | Примеры | Методики | Форум | Download | |

|
|
Наиболее очевидным способом минимизации СДНФ (совершенной дизъюнктивной нормальной формы логической функции: "дизъюнктивной" как сумма произведений; "совершенной", так как в каждое произведение входят все переменные; "нормальной", поскольку в любом произведении каждая переменная встречается лишь однажды) является выполнение преобразований, аналогичных преобразованиям обычной алгебры. Это возможно, поскольку для операций И и ИЛИ справедливы законы ассоциативности (сочетательный) и дистрибутивности (распределительный). Другими словами, аргументы можно группировать, а общие аргументы - выносить за скобки. Речь идёт о том, чтобы перейти от СДНФ к ДНФ с минимумом слагаемых, при этом количество множителей в каждом слагаемом должно быть также минимальным (избавиться от "совершенства"), то есть максимально уменьшить количество переменных и операций в СДНФ. В преобразованиях алгебры логики применяют следующие соотношения, которые легко доказать с помощью таблиц истинности:
( Здесь a - аргумент, который может пронимать любое значение: 0 или 1.) Упростим функцию непосредственно с помощью алгебраических преобразований с использованием логических тождеств:
Запишем СДНФ:
Вынесем за скобки произведение x и y из второй и
четвёртой слагаемых конъюнкций и произведение y
и
Воспользуемся тождествами:
и получим "минимальную" ДНФ:
При большом количестве переменных и операций иногда трудно прийти сразу же к "минимальной" ДНФ, поэтому используют и другие способы минимизации функций, которые мы и рассмотрим далее. Целью минимизации логической функции в строгом понимании этого термина является нахождение минимальной ДНФ или одной из минимальных ДНФ, если их несколько. Какого-либо правила группировки, гарантированно приводящего любую ДНФ к её минимальной форме, не существует. Приходится пробовать различные варианты и сравнивать результаты. Процедуру поиска заметно облегчают специально разработанные методы минимизации. Минимизация логических функций с помощью графического представления n-мерного куба. Минимизацию функций трёх или даже четырёх переменных можно эффективно выполнять, используя геометрическое представление логической функции. Все возможные комбинации значений n аргументов представляются как вершины n-мерного куба. Вершины, в которых функция равна единице, выделяются. Штрих справа от имени переменной означает её отрицание, для конъюнкции служит обычный знак умножения. 1. Минимизируем функцию:
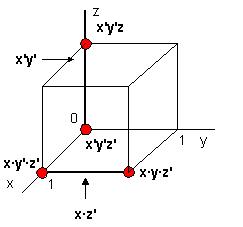
Рис. 1 Единичные значения показаны жирными точками. Вершины куба соответствуют трёхчленным конъюнкциям аргументов, то есть трёхчленным элементарным конъюнкциям СДНФ, рёбра соответствуют двухчленным элементарным конъюнкциям ДНФ, полученным в результате минимизации СДНФ, а грани - единичному или нулевому значению какой-либо одночленной элементарной конъюнкции минимизированной ДНФ. Из рисунка(1) видно, что две соседние вершины, например xy'z' и xyz', можно склеить. Формула ребра для оси-переменной не содержит этой переменной, так как значение функции на "склеенных" им вершинах не зависит от значения этой переменной, что соответствует операции выноса за скобки общего множителя. Например, ребро xz' соединяет точки xy'z' и xyz': ( xy'z')+( xyz') = xz' (y'+y) = xz' Минимизация с помощью n-мерного куба сводится к объединению максимума вершин, на которых функция принимает единичные значения, в минимум рёбер. Значит, минимальная ДНФ имеет вид:
2. Минимизируем функцию, состоящую из пяти членов:
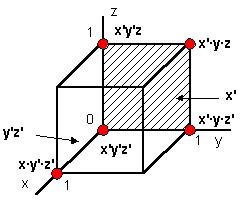
Рис. 2 На рисунке(2) четыре вершины образуют грань куба. Формула этой грани состоит только из одной переменой - x', ось которой пересекает эта грань. В результате функция вместо пяти точек будет представлена гранью и ребром:
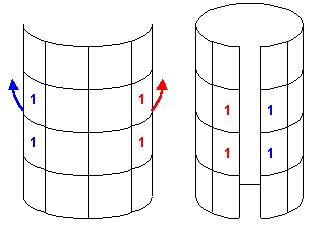
3. Функции четырёх переменных можно представить в виде двух связанных кубов: одного - для нулевого значения четвёртого аргумента, а другого - для единичного. Кубы можно располагать один внутри другого, тогда отрицание четвёртой переменной определяется на вершинах внутреннего куба, вставленного во внешний. Значения других переменных определены на обоих кубах идентично.
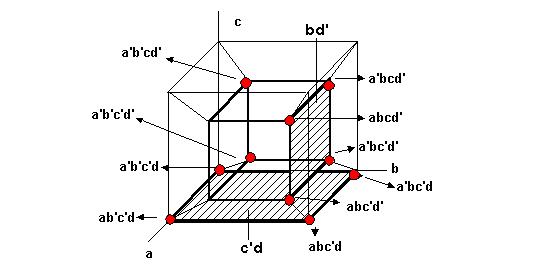
Рис. 3 Как и в трёхмерном кубе, минимизация выполняется выявлением замкнутых граней, рёбер или целых замкнутых объёмов. Сначала рассмотрим "неудачный" вариант минимизации - объединение точек a'b'cd' и a'b'c'd' в ребро. При этом мы получим, что ДНФ функции равна: F(a,b,c,d)=a'b'd'+bd'+c'd. Но эта ДНФ не минимальна (её можно ещё упростить), так как точки a'b'cd', a'b'c'd', a'bcd' и abcd' образуют грань куба (её формула a'd'). Значит, минимальная ДНФ равна:F(a,b,c,d)= a'd'+bd'+c'd. При пяти аргументах нужно рисовать четыре куба, поэтому при пяти и более аргументах метод становится громоздким и теряет наглядность. Минимизация логических функций методом Карно. При числе аргументов 3,4 и даже 5 хорошо работает метод минимизационных карт Карно-Вейча (или карт Карно), основанный на зрительном анализе развёрток многомерных кубов на плоскости.
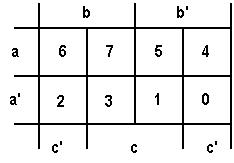
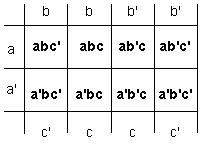
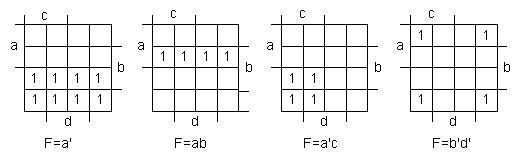
Рис. 4 На рисунке (4) представлена нумерация клеток в карте Карно. Номер каждой клетки соответствует номеру строки в таблице истинности функции. Каждая клетка диаграммы соответствует логическому произведению прямого или инверсного значения переменных, присвоенных столбцу или строке, на пересечении которых она находится.
Рис. 5 Например, клетка с номером 1 находится на пересечении строки со значением переменной a' и столбца со значениями переменной b' и с и соответствует логическому произведению a'b'с (рис. 4 и 5). В диаграммах Карно значения переменных присваиваются таким образом, чтобы соседние клетки по строкам и столбцам отличались между собой значением только одной переменной. Клетки, находящиеся на границах одной строки или столбца, считаются соседними. По описанию логической функции нескольких переменных на диаграммах Карно в клетки записывают значения логических произведений из таблицы истинности. Минимизируем функцию трёх переменных с помощью диаграммы Карно. F (a, b, c)=a'b'c+a'bc+a'b'c'+a'bc'+ab'c'
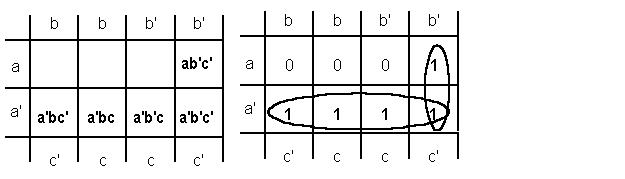
Рис.6 На рисунке (6) представлена диаграмма Карно, соответствующая логической функции F(a, b, c). Диаграммы Карно позволяют выделить произведения, которые можно упростить. Если произведения стоят в соседних клетках, то из общего выражения можно исключить одну переменную. Например, элементы 0 и 4 клеток (рис. 4 и рис. 6) можно преобразовать к виду: ab'c'+a'b'c'=b'c'(a+a')=b'c'. А если произведения образуют строку (или столбец), то исключаются аргументы, встречающиеся в прямом или инверсном кодах. В нашем случае строка после упрощения будет иметь значение a', так как не зависит от других значений переменных. Одно и то же произведение можно использовать несколько раз в комбинации с другими переменными. Значит, наша функция после упрощения будет иметь вид: F (a, b, c)= b'c'+ a'. Теперь рассмотрим минимизацию функции, состоящей из четырёх переменных.
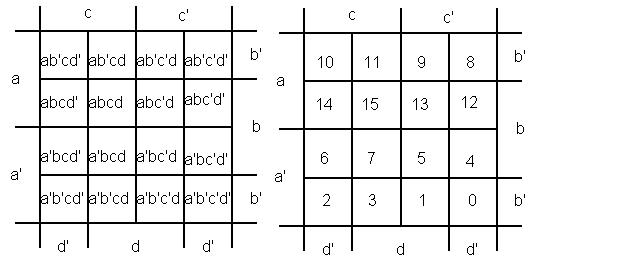
Рис. 7 На рисунке (7) справа представлена нумерация клеток в карте Карно для функции из четырёх переменных. Минимизируем функцию F(a,b,c,d) = a'b'cd' + a'b'c'd' + a'b'c'd + ab'c'd + + a'bcd' + abcd' + a'bc'd' + a'bc'd + abc'd' + abc'd.
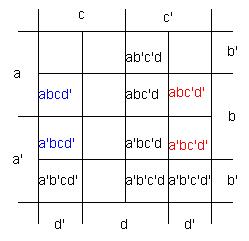
Рис. 8 Произведения, образующие квадрат (с учётом замкнутости краевых линий диаграммы), позволяют исключить из общего выражения две переменные.
Рис. 9 Произведения abcd', a'bcd', abc'd', a'bc'd' образуют квадрат, поэтому можно исключить из общего выражения две переменные (после упрощения получаем bd'). В нашем случае клетки карты Карно можно объединить в два квадрата (abcd', a'bcd', abc'd', a'bc'd' и a'b'c'd', a'b'cd', a'bc'd', a'bcd') и строку c'd. То есть минимальная ДНФ функции имеет вид: F (a, b, c, d)= a'd'+bd'+ c'd. Основные варианты группирования клеток на диаграммах Карно:
Минимизация логических функций методом Куайна -- Маккласки. Вернёмся теперь к функции Заметим, что объединение двух смежных вершин в
ребро, соответствующее выносу общего множителя
за скобки, в таблице истинности означает
объединение двух строк в одну. В комбинируемых
строках должны совпадать все значения
переменных, кроме одной - сравниваемые строки
отличаются на одну единицу. Значение не
совпавшей переменной безразлично и может быть
обозначено "
можно заменить одной строкой:
так как в этой строке значение переменной B не влияет на единичность функции.
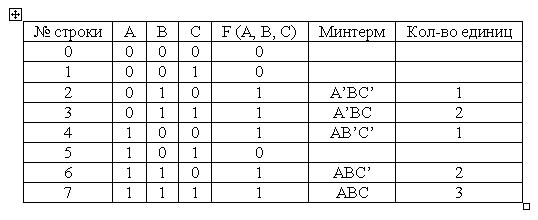
1. Запишем таблицу истинности функции F(A,B,C):
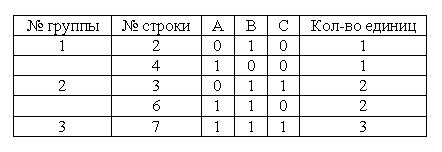
2. Сгруппируем минтермы по количеству единиц в них:
3. Произведём первое объединение строк каждых предыдущих и последующих групп:
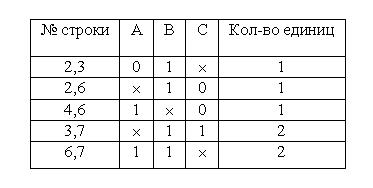
4. Объединим строки с совпадающими позициями "крестиков":
5. Из двух строк с идентичными значениями минтермов оставляем только одну: F (A, B, C)=AC'+B
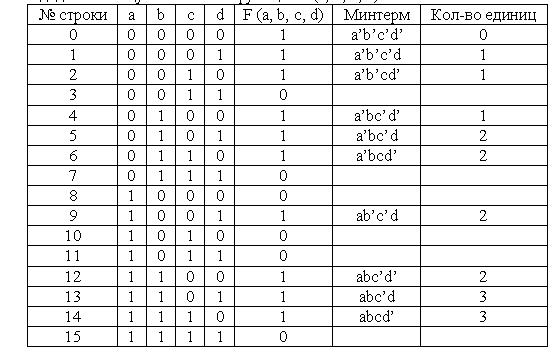
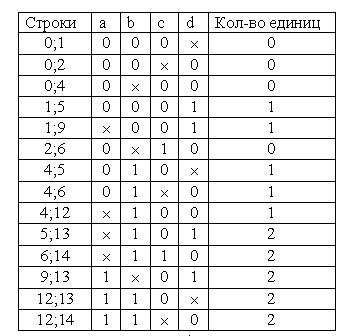
1. Создадим таблицу истинности функции F(a, b, c, d):
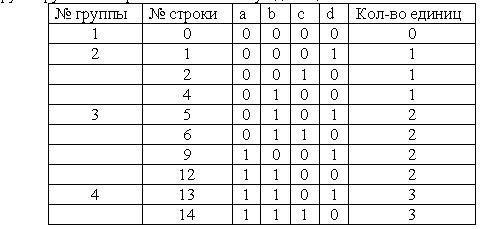
2. Сгруппируем минтермы по количеству единиц в них:
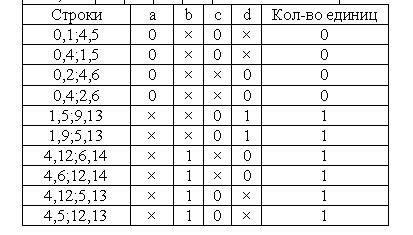
3. Произведём первое объединение строк каждых предыдущих и последующих групп:
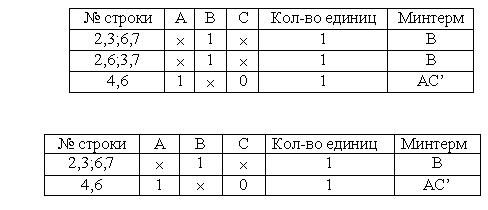
4. Объединим строки с совпадающими позициями "крестиков":
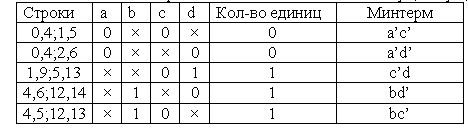
5. Из двух строк с одинаковыми значениями переменных оставляем только одну (любую):
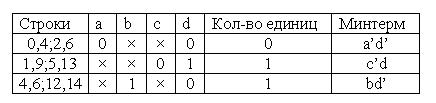
6. Обратим внимание на то, что первый минтерм избыточен, так как 0-я и 4-я строки уже вошли в комбинацию со 2-ой и 6-ой (второй минтерм), а 1-я и 5-я - с 9-ой и 13-ой соответственно (третий минтерм). Пятый минтерм также избыточен, так как 4-я; 5-я; 12-я и 13-я строки уже сгруппированы с 6-ой и 0-ой (четвёртый и второй минтермы); с 13-ой (третий минтерм); с 14-ой (четвёртый минтерм) и с 5-ой (третий минтерм) соответственно. Поэтому удаляем первую и пятую строки из таблицы и записываем минимальную ДНФ:
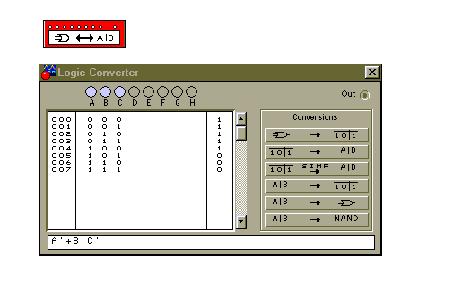
F(a, b, c, d)= a'd'+ c'd+ bd'. Метод минимизации Куайна - Маккласки лежит в основе работы логического конвертора (Logic Converter) Electronics Workbench 5.12. Найдём минимальную ДНФ функции, заданной графически на рисунке 2. Перепишем правую часть СДНФ в верхнем регистре, прописными буквами: A'B'C+A'BC'+A'B'C'+A'BC+AB'C' Скопируем и вставим в строку формулы конвертора:
Теперь восстановим по формуле таблицу истинности (4-я кнопка) и упростим таблицу, получив в строке формулы минимальную ДНФ (3-я кнопка):
Итак, минимальная ДНФ функции F(A, B, C)= A'+B'C'. Для минимизации функций и поиска наиболее экономичной схемы, реализующей заданное выражение, до сих пор не найдено эффективных алгоритмов, позволяющих решать эти задачи целенаправленно и быстро. Найти гарантированно минимальное выражение для произвольной функции можно лишь методом полного перебора вариантов различных способов группировки в процессе минимизации, а это реально осуществимо лишь при небольшом числе аргументов. С ростом их числа сложность минимизации и поиска экономичной схемы растёт экспоненциально и очень скоро становится не под силу ни человеку, ни ЭВМ. При числе переменных - 6 минимизируем функцию с помощью представления трёхмерного куба.
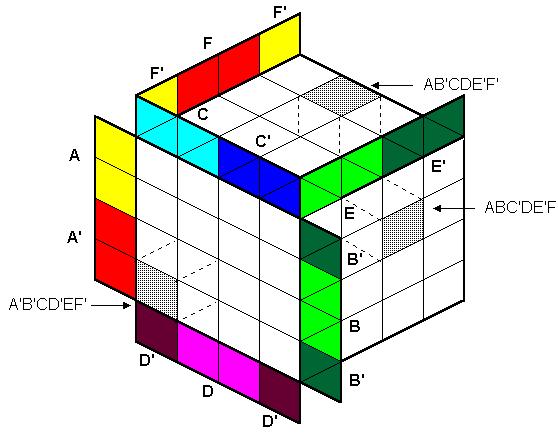
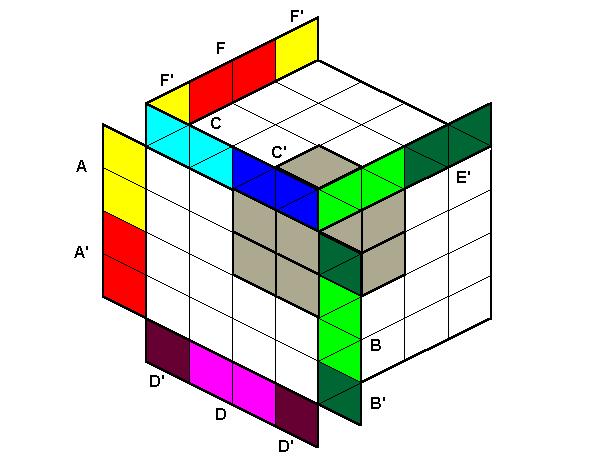
Рис. 10 На рисунке каждый маленький трёхмерный кубик диаграммы соответствует логическому произведению прямого или инверсного значения переменных, присвоенных столбцу или строке, на пересечении которых он находится. Рассмотрим пример минимизации функции F(A, B, C, D, E, F) =
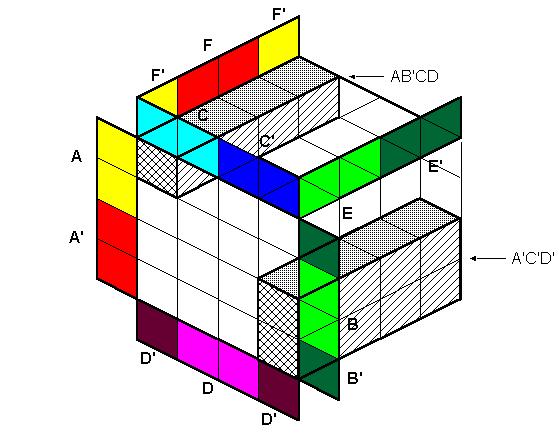
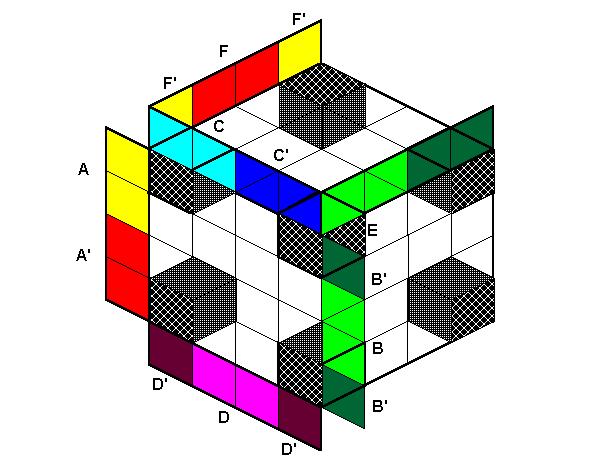
Рис.11 Из рисунка (11) видно, что из произведений, образующих столбец (или строку) можно исключить две переменные, а из произведений, образующих две строки (два столбца),-- три переменные. Таким образом получаем: F (A, B, C, D, E, F)= A' C'D'+A B'CD'. Основные варианты группировки "кубиков": 1. Если кубики диаграммы образуют куб, то из произведения исключаются три переменные (смотри рис. 12).
Рис. 12 2. Если кубики диаграммы образуют столбец (или строку), то можно исключить две переменные (смотри рис. 11). 3. Если кубики диаграммы образуют два столбца (две строки), то исключаются три переменные (смотри рис. 11). 4. Если кубики диаграммы образуют три столбца (три строки), то исключаются четыре переменные. 5. Если кубики диаграммы образуют четыре столбца (четыре строки), то исключаются четыре переменные. 6. Если кубики диаграммы находятся в углах диаграммы, то исключаются три переменные (смотри рис.13).
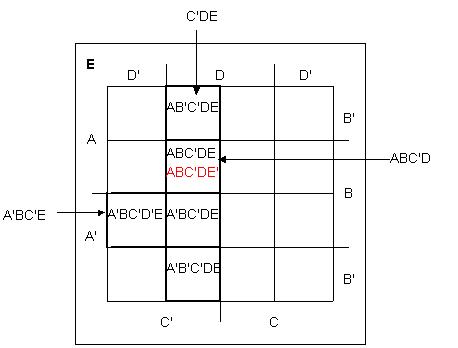
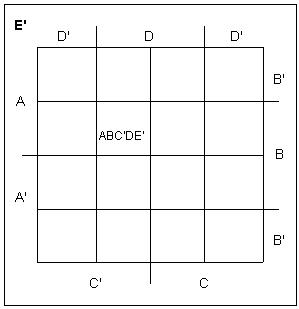
Рис. 13 Пять переменных. Рассмотрим пример: Минимизируем функцию F(A, B, C, D, E) = AB'C'DE + A'BC'D'E + A'B'C'DE + A'BC'DE + ABC'DE + ABC'DE'.
Рис. 14 Видно, что если клетки диаграммы образуют столбец, то исключаются две переменные. А из двух клеток можно исключить одну переменную. Таким образом, получаем: F (A, B, C, D, E) = A'BC'E + ABC'D + C'DE.
Содержание |
| | На первую страницу | Поиск | Купить Matlab | |
|
|