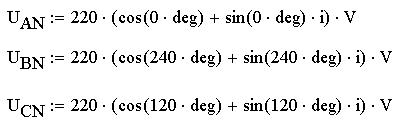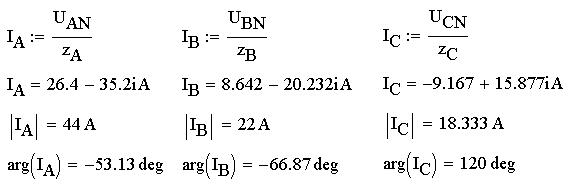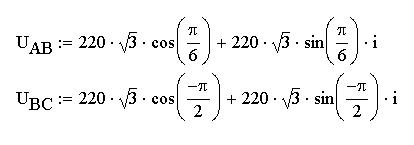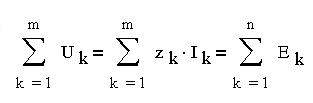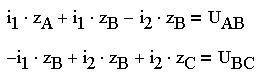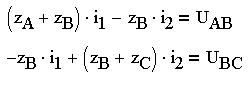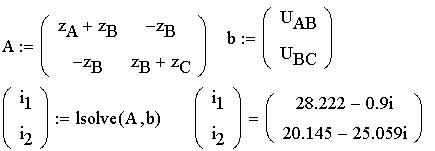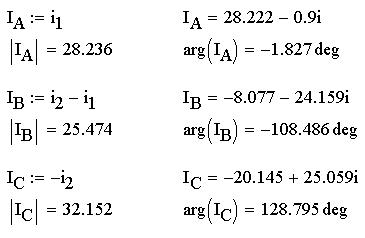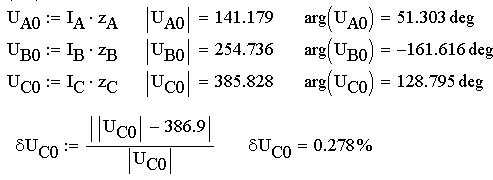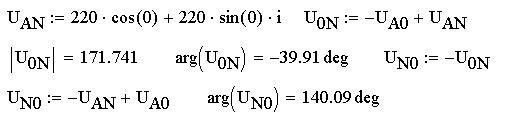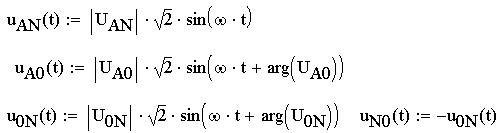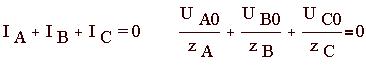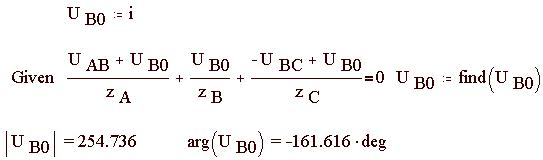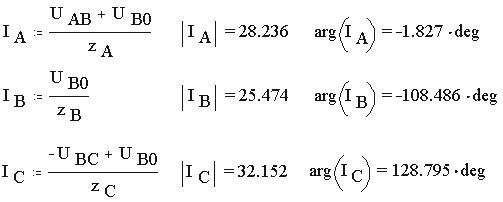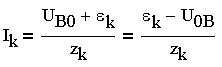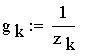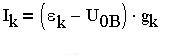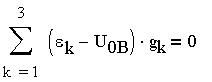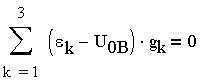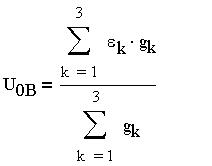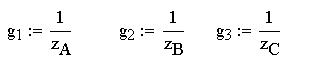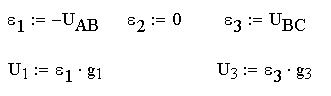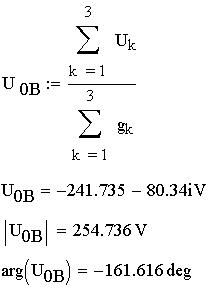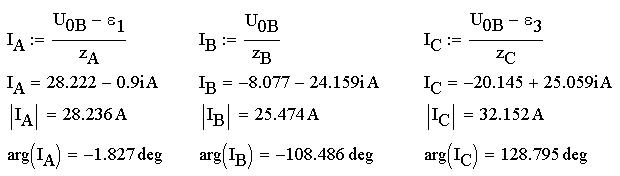Вернуться на страницу <Методические разработки>
Содержание

Творческий проект по предмету
"Информационные и электронные технологии".

СОДЕРЖАНИЕ:

1. Введение: трехфазные системы.
2. Основная часть: Соединение источника энергии и приемника по схеме звезда.
   2.1 Расчет электрической цепи без обрыва.
   2.2 Обрыв нулевого провода.
       2.2.1 Метод контурных токов.
       2.2.2 Расчет по первому закону Кирхгофа.
       2.2.3 Метод двух узлов.
   2.3 Расчет цепи при обрыве нулевого провода и линейного провода C.
3. Заключение.
4. Литература.

1. ВВЕДЕНИЕ

Объединение в одну цепь нескольких подобных по структуре цепей синусоидального тока одной частоты с независимыми источниками энергии широко применяется в технике. Объединяемые цепи синусоидального тока принято называть фазами, а всю объединённую систему цепей - многофазной системой. Наибольшее распространение получила трёхфазная система.

Трёхфазная система была изобретена и разработана во всех деталях, включая трёхфазные трансформатор и асинхронный двигатель, русским инженером М. О. Доливо-Добровольским в 1891 году. В настоящее время для передачи и распределения энергии в подавляющем большинстве случаев применяются трёхфазные системы. Очень важным преимуществом трёхфазной системы является также исключительная простота и дешевизна трёхфазных асинхронных двигателей.

Источником энергии в трёхфазной системе служит трёхфазный генератор. Он отличается от однофазного генератора синусоидального тока тем, что в пазах его статора размещены не одна, а три электрически изолированные друг от друга обмотки - фазные обмотки генератора. Если ротор генератора двухполюсный, то оси фазных обмоток генератора повернуты в пространстве относительно друг друга на угол 2/3. При вращении ротора в фазных обмотках статора индуктируются синусоидальные фазные ЭДС. Вследствие симметрии конструкции генератора максимальные Еm и действующие Еф значения ЭДС во всех фазах одинаковые. Однако линии магнитного поля вращающегося ротора пересекают провода фазных обмоток не одновременно. Поэтому синусоидальные ЭДС обмоток сдвинуты по фазе относительно друг друга на одну треть периода, чему соответствует пространственный угол 2/3 между осями обмоток.

Для получения трёхфазной системы необходимо определённым образом соединить фазы источника энергии и фазы приёмника. Возможны два основных способа соединения в трёхфазной системе: соединение источника энергии и приёмника по схеме звезда и соединение источника энергии и приёмника по схеме треугольник.

2. ОСНОВНАЯ ЧАСТЬ

Соединение источника энергии и приемника по схеме звезда.

У источника энергии и приемника, выполненных по схеме звезда, все концы фазных обмоток генератора соединяются в общий узел N; такой же узел n образует соединение трех фаз приемника, а три обратных провода фаз системы объединяются в один нейтральный провод. Остальные три провода, соединяющие генератор с приемником, называются линейными. Узел, который образуют обмотки фаз генератора или фазы приемника, называется нейтралью или нейтральной точкой.

Приемники энергии, которые не могут обеспечить строго равномерной нагрузки фаз, включаются звездой с нулевым проводом.

2.1 Расчет электрической цепи без обрыва.

Определим численные значения сопротивлений фаз и фазные напряжения:

Теперь по закону Ома найдем фазные токи IA,IB и IC:

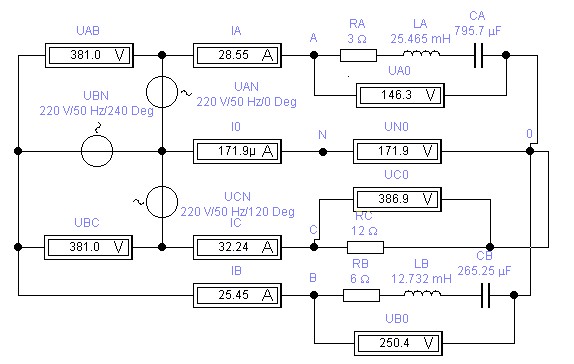
Задача решена.

2.2 Обрыв нулевого провода.

Обрыв нулевого провода при симметричной системе фазных э. д. с. генератора и неодинаковых сопротивлениях фаз приемника из-за смещения нейтрали влечет за собой изменение фазных токов и напряжений приемника.

Изменение же фазных напряжений совершенно недопустимо. Поэтому в нейтральных проводах никогда не устанавливают предохранители. При изменении фазных напряжений в одних фазах может наблюдаться недокал, а в других фазах - перекал и быстрое перегорание ламп. Если при таком соединении перегорит один из магистральных предохранителей, то отключатся лампы только одной (соответствующей) фазы. Изменение же фазных напряжений совершенно недопустимо. Поэтому в нейтральных проводах никогда не устанавливают предохранители. При изменении фазных напряжений в одних фазах может наблюдаться недокал, а в других фазах - перекал и быстрое перегорание ламп. Если при таком соединении перегорит один из магистральных предохранителей, то отключатся лампы только одной (соответствующей) фазы.

Воспользуемся методом контурных токов для расчета токов и напряжений в трехфазной цепи при аварийном обрыве нулевого провода, как на виртуальной модели в Electronics Workbench 5.12 ниже:

Модель трехфазной цепи при аварийном обрыве нулевого провода:

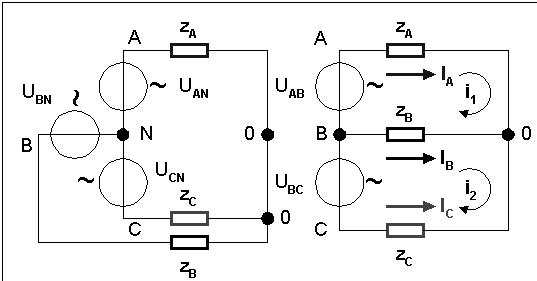
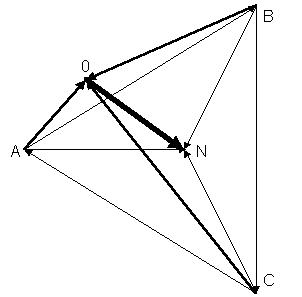
На рисунке ниже показана условная схема цепи с обрывом нулевого провода и её эквивалентная схема: фазные нагрузки оказались включенными под линейные напряжения UAB и UBC.

Определим численные значения сопротивлений фаз zA, zB и zC, линейных напряжений UAB и UBC и составим систему из двух уравнений относительно неизвестных контурных токов i1 и i2. Как видно на схеме виртуальной модели, нулевая начальная фаза определена для фазного напряжения UAN трехфазного источника напряжения, относительно которого начальные фазы линейных напряжений составляют, соответственно, +30о и -90о:

2.1.1 Метод контурных токов.

На данном примере рассмотрим метод контурных токов. Этот метод был разработан Максвеллом. Для контурных токов должен выполняться второй закон Кирхгофа (закон Кирхгофа для напряжений): в любом контуре схемы электрической цепи алгебраическая сумма напряжений на всех резистивных элементах равна алгебраической сумме ЭДС:

где m - число резистивных элементов в контуре, n - число ЭДС.

Для начала установим направления контурных токов, так как иначе нельзя составить уравнения ни по первому, ни по второму законам Кирхгофа. Если считать ток алгебраической величиной, которая может принимать как положительные, так и отрицательные значения, то можно выбрать для каждого тока произвольное направление. Это направление называют положительным. При этом положительное направление во всех контурах цепи должно быть одинаковым. Пусть в нашей цепи контурные токи будут направлены по часовой стрелке. На условной схеме цепи положительные направления показаны тонкими стрелками. Теперь для первого и второго контуров запишем уравнения, учитывая направления контурных токов.

Эта система уравнений является математической формулировкой метода контурных токов. Так как число контурных токов всегда меньше числа токов в ветвях, то применение этого метода уменьшает число неизвестных величин в решаемой системе уравнений.

Также эту систему можно записать следующим образом:

Определим матрицу A коэффициентов при неизвестных, вектор-столбец b свободных членов уравнений, а также вектор-столбец решений, который найдем с помощью встроенной функции lsolve(A,b):

Определим фазные токи IA, IB и IC через контурные i1 и i2 и найдем их:

Согласно закону Ома определим и найдем фазные напряжения; сравнивая также рассчитанное напряжение UC0 с показанием соответствующего прибора на виртуальной модели, определим относительную погрешность этого показания относительно рассчитанного:

Определим теперь напряжение "смещения нуля относительно нейтрали" N генератора U0N. Для этого определим напряжение фазной обмотки генератора UAN, затем найдем величину, численно равную работе по переносу +1 Кл от 0 до N по одному из возможных "маршрутов", например: 0 ® A ® N, т. е. напряжение U0N как сумму напряжений U0A = - UA0 и UAN:

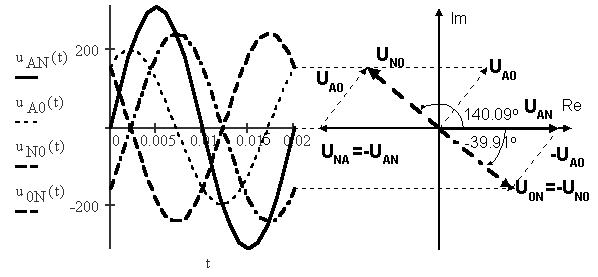
Определим функции мгновенных значений линейного напряжения uAN(t), фазного uA0(t) и напряжений u0N(t) и uN0(t), затем создадим график, по которому построим векторную диаграмму:

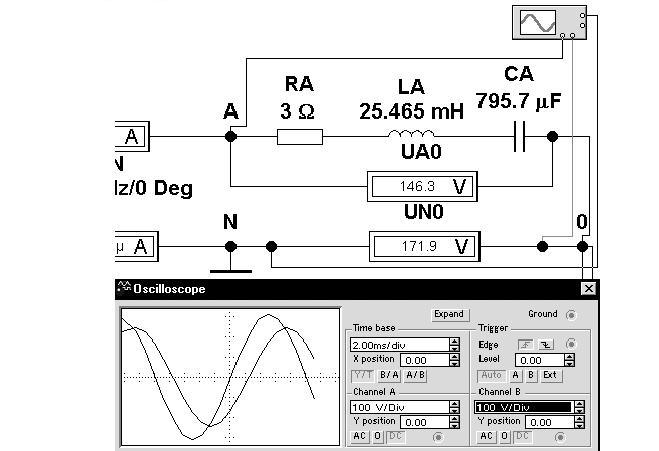
Получим осциллограммы напряжений uAN(t) и u0N(t) на виртуальной модели. Для этого условный нулевой уровень отсчета ("землю") присоединим к нейтрали, к ней жеприсоединим клемму заземления осциллографа. На канал А осциллографа подадим потенциал точки А схемы, на канал В - точки 0:

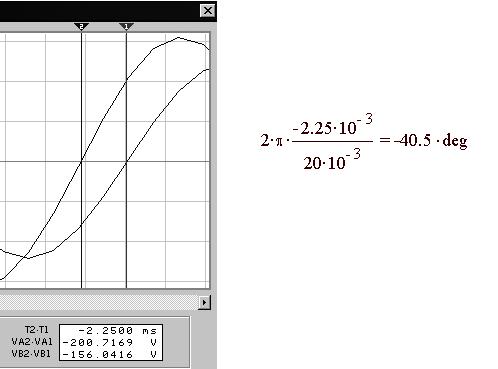
По временным диаграммам определим сдвиг фаз между u0N(t) и uAN(t).

Временной сдвиг составляет, как это видно на рисунке слева, -2.25 мс, что соответствует фазовому сдвигу:

Найдем в Mathcad этот же сдвиг фаз как разность аргументов соответствующих векторов:

Определение напряжений между отдельными точками цепи может быть сделано с большой простотой и наглядностью графически, путем построения особой векторной диаграммы, называемой топографической. Топографическая диаграмма строится таким образом, чтобы каждой точке цепи соответствовала определенная точка на диаграмме, чтобы вектор, проведенный в эту точку из начала, выражал по величине и фазе потенциал соответствующей точки цепи. При этом условии отрезок, соединяющий любые точки на диаграмме, по величине и фазе определяет напряжение между соответствующими точками цепи.

Представим фазные и линейные напряжения генератора, фазные напряжения нагрузок и напряжение смещения нуля на единой топографической векторной диаграмме, которую создадим в приложении VISIO Express Drawing 3.0:

2.1.2 Расчет по первому закону Кирхгофа.

Рассмотренную цепь также можно рассчитать, начав с записи уравнения непрерывности токов (первый закон Кирхгофа) для узла 0 (см. условную схему цепи, а также векторную диаграмму напряжений выше):

Выбрав в качестве единственной неизвестной напряжение, например, UB0 при заданных как выше сопротивлениях ветвей и линейных напряжениях, получаем уравнение с одной неизвестной, численное решение которого находим в Mathcad:

Теперь дополнительно, по закону Ома, определяем и находим токи ветвей:

Продолжение решения этой задачи аналогично.

2.1.3 Метод двух узлов.

Рассмотрим ещё один способ расчета предложенной цепи. Исследуемая электрическая цепь содержит только два узла. Наиболее простым методом расчета в этом случае является метод двух узлов (узлового напряжения).

Наша цепь состоит из узлов B и 0 и трех ветвей. Так как ветви между узлами B и 0 соединены параллельно, то разность потенциалов или напряжение между этими узлами можно выразить через ЭДС, ток и сопротивление резистивного элемента любой из ветвей. По обобщенному закону Ома:

откуда узловое напряжение цепи:

Определим теперь проводимость цепей:

На основании этих соотношений ток

В цепи все ЭДС направлены к узлу 0 и положительное направление каждого тока совпадает с направлением ЭДС в ветви, т.е. все токи направлены к тому же узлу. По первому закону Кирхгофа алгебраическая сумма токов в узле цепи равна нулю:

т.е.:

и, следовательно:

откуда узловое напряжение определяется через параметры элементов цепи:

здесь со знаком плюс записываются ЭДС, действующие к узлу 0.

Зная напряжение между узлами, легко определить ток в любой ветви. Зная токи, мы можем вычислить линейные и фазные напряжения.

Решим нашу задачу, применяя этот метод. Как и в предыдущих решениях, определим сопротивления фаз zA, zB и zC и линейные напряжения UAB и UBC:

Теперь выразим узловое напряжение UB0 через параметры ветвей цепи. Для этого определим проводимости ветвей и их ЭДС:

В схеме цепи было принято, что все ЭДС направлены к узлу 0 и все токи направлены к тому же узлу.

Теперь определим и вычислим узловое напряжение U0B:

Зная узловое напряжение в цепи, можно вычислить токи её ветвей по обобщенному закону Ома для неразветвленного участка цепи:

Продолжение решения этой задачи аналогично двум предыдущим.

ЗАКЛЮЧЕНИЕ

Таким образом, изучение работы трехфазных цепей очень важно для народного хозяйства нашей страны и для практического использования асинхронных двигателей во всем мире. Трехфазные генераторы синусоидального переменного тока широко используются повсеместно и по сей день, и зарекомендовали себя как надежные и простые в использовании системы снабжения электроэнергией.

ЛИТЕРАТУРА

1. Edminister, Josef. Schaum's Outline of Theory and Problems of Electric Circuits. Second Edition./McGraw-Hill, Inc., 1995.
2. Ходяков И. А. Основы электротехники. Часть II. Под ред. И.П. Дешко. Учебное пособие /МГДТДиЮ, МИРЭА - М., 1998, 38с.
3. Сборник творческих проектов учащихся 1998/99 уч. года. Под ред. И.А. Ходякова/ МГДТДиЮ, МИРЭА - М., 1999, 50с.
4. Калашников С. Г. Электричество. Издательство "Наука". - М., 1970, 666с
5. Мансуров Н.Н., Попов В.С. Теоретическая Электротехника. "Госэнэргоиздат". Издание 7ое, - Лен., 1958., 608с.

Содержание
Вернуться на страницу <Методические разработки>