Вернуться
на страницу <Методические разработки>
Содержание
Творческий проект по предмету
"Информационные и электронные технологии"
Школа №1006.
11 "В" и 11"Д" классы.
Харлова Евгения и Минаева Елена.
Моделирование
трёхфазного синусоидального тока по
схеме "Звезда"
Запишем данные задачи:
Нахождение токов (J. Edminister) по закону Ома в экспоненциальной форме:
Пример решения вопросов по
зачётной работе
Определим сопротивление ветви
A0 цепи в тригонометрической и экспоненциальной форме и найдём значения модуля и угла :
Определим сопротивление ветви
B0 цепи в тригонометрической и экспоненциальной форме и найдём значения модуля и угла :
Определим сопротивление ветви
C0 цепи в тригонометрической и экспоненциальной форме и найдём значения модуля и угла :
Определим и найдём фазное напряжение в обмотке генератора AN
в тригонометрической и экспоненциальной форме :
Определим и найдём фазное напряжение в обмотке генератора
BN в тригонометрической и экспоненциальной форме :
Определим и найдём фазное напряжение в обмотке генератора
CN в тригонометрической и экспоненциальной форме :
Построим в VISIO Express Drawing 2.0 векторную диаграмму напряжений :
Если нулевой провод не оборван,то фазное напряжение
UAB равно напряжению обмотки генератора
UAN (далее рассмотрится обрыв нуля).
По закону Ома определим и найдём действующее значение тока, его модуль и угол
IA :
По закону Ома определим и найдём действующее значение тока, его модуль и угол
IB :
По закону Ома определим и найдём действующее значение тока, его модуль и угол IC :
По уравнению непрерывности токов определим и найдём действующее значение тока в нулевом проводе, его модуль и угол :
Построим в VISIO Express Drawing 2.0 векторную диаграмму токов :
Определим имена размерностей полной и реактивной мощностей в СИ через встроенные :
Рассчитаем полную мощность через реативную и активную мощности :
Определим и найдём полную мощность на ветви
A0 через напряжение и тока на этой ветви :
Определим и найдём активную мощность на ветви
A0 :
Определим и найдём реактивную мощность на ветви
A0 :
Определим и найдём значение cos(фIU) между активной и полной мощностями на ветви A0 :
Определим и найдём полную мощность на ветви
B0 через напряжение и тока на этой ветви :
Определим и найдём активную мощность на ветви
B0 :
Определим и найдём реактивную мощность на ветви
B0 :
Определим и найдём значение cos(фIU) между активной и полной мощностями на ветви B0 :
Определим и найдём полную мощность на ветви
C0 через напряжение и тока на этой ветви :
Определим и найдём активную мощность на ветви
C0 :
Определим и найдём реактивную мощность на ветви
C0 :
Определим и найдём значение cos(фIU) между активной и полной мощностями на ветви C0 :
Определим и найдём значение полной мощности через сумму всех полных мощностей :
Определим и найдём значение активной мощности через сумму всех активных мощностей :
Определим и найдём значение реактивной мощности через сумму всех реактивных мощностей :
Построим в VISIO Express Drawing 2.0 векторную диаграмму мощностей :
Виртуальная модель с измерением ваттметрами в фазных мощностях в Multisim 2001 Student :
Определим частоту и угловую частоту:
Определим и найдём значение активного сопротивления, соответствующего резистору на электронной модели, в фазе A :
Определим и найдём значение активного сопротивления,
соответствующего резистору, и индуктивность на электронной модели в фазе B :
Определим и найдём значение активного сопротивления,соответствующего резистору, и индуктивность на электронной модели в фазе C :
Создадим в Electronics Workbench 5.12 электронную модель источника трехфазного напряжения синусоидального тока, использовав виртуальные модели источников напряжений однофазного синусоидального тока:
Обрыв нулевого провода Создадим в Electronics Workbench 5.12 электронную модель источника трехфазного напряжения синусоидального тока, использовав виртуальные модели источников напряжений однофазного синусоидального тока, с обрывом нуля :
Определим напряжения на участках цепи AB , BC и CA :
Рассмотренную цепь можно рассчитать, начав с записи уравнения непрерывности токов (1-е правило Кирхгофа) для узла нуль (см. эквивалентную схему цепи и векторную диаграмму ниже):
Выбрав в качестве единственной неизвестной напряжение, например, UA0
при заданных выше сопротивлениях ветвей и линейных напряжениях, получим уравнение с одной неизвестной, численное решение которого находим в MathCAD:
Зададим предварительное приближение UA0: = i
Воспользуемся функцией root для решения уравнения:
Найдём напряжение,модуль и значение угла в фазе A0 :
По закону Ома для участка цепи определим и найдём модуль и значение угла тока IA :
Определим напряжение на участке цепи B0
:
Найдём значение напряжения,модуль и угол на участке цепи B0
:
По закону Ома для участка цепи определим и найдём модуль и значение угла тока B0 :
Определим напряжение на участке цепи C0
:
Найдём значение напряжения,модуль и угол на участке цепи C0
:
По закону Ома для участка цепи определим и найдём модуль и значение угла тока C0 :
Определим напряжение нуля относительно нейтрали 0N :
Найдём значение напряжения,модуль и уголь на участке цепи 0N
:
Поместим показания осциллографа из Electronics Workbench 5.12 для сравнения с графиком и результатами полученными в
Mathcad.
Определим период и угол сдвига фазы 0N
относительно AN :
Найдём значение угола сдвига фазы 0N
относительно AN :
Найдём в Mathcad этот же сдвиг фаз как разность аргументов соответствующих векторов :
Определим время как дискретный аргумент :
Определим функции мгновенных значений напряжений нуля и нейтрали ( uAN(t) , u0N(t) ) :
Построим график мгновенных значений напряжений нуля и нейтрали :
Построим в VISIO Express Drawing 2.0 векторную диаграмму напряжений со смещением нуля относительно нейтрали :
Построим эквивалентную схему цепи, построенной выше :
Определим IA , IB и IC и начальные приближения решений этих токов источника напряжения , как мнимые единици i :
Воспользуемся математической функцией :
По первому закону Кирхгофа:
По второму закону Кирхгофа:
После применения законов Кирхгофа, определим и найдём с помощью функции Given... find токи A,B и C :
Найдём вектор-столбец модулей токов и вектор-столбец их начальных фаз :
Определим напряжения на участках цепи AB и BC по методу контурных токов:
Определим матрицу A коэффициентов при неизвестных и вектор-столбец b свободных членов :
Затем применим встроенную функцию lsolve ( A , b ) и найдём контурные токи :
Определим и найдём значение и модуль контурного тока на участке цепи A :
Определим и найдём значение и модуль контурного тока на участке цепи B :
Определим и найдём значение и модуль контурного тока на участке цепи C :
Найдём значение угла начальных фаз контурных токов IA , IB и IC :
Согласно закону Ома, определим и найдём модуль и значение угла фазного напряжения на участке цепи A0 :
Согласно закону Ома, определим и найдём модуль и значение угла фазного напряжения на участке цепи B0 :
Согласно закону Ома, определим и найдём модуль и значение угла фазного напряжения на участке цепи C0 :
А теперь мы можем воспользоваться методом двух узлов для нахождения напряжений между узлами:
Так как ветви между узлами B и 0
соединены параллельно, то разность потенциалов или напряжение между этими узлами можно выразить через ЭДС Ek , ток Ik и сопротивление резистивного элемента zk любой из ветвей .По обобщённому закону Ома :
откуда :
где узловое напряжение UB0 .
На основании этих соотношений ток будет равен :
где gk -проводимость k-й ветви :
По первому закону Кирхгофа алгеброическая сумма токов в узле цепи равна нулю:
и, следовательно :
Узловое напряжение определяется через параметры элементов цепи :
Определим массив напряжения:
Определим проводимости ветвей :
Определим узловое напряжение B0 :
Найдём значение, модуль и величину угла узлового напряжения B0 :
Обрыв нулевого и линейного
провода А Оборвем линейный провод А и заменим оборванный нулевой провод вольтметром с внутренним сопротивлением 1MОм для измерения напряжения смещения нуля относительно нейтрали :
Сопротивление на участке BC , очевидно, равно сумме сопротивлений на участке B и C :
Определим ток на участке цепи BC :
Найдём величину, модуль и значение угла тока на участке цепи BC :
Определим напряжение на участке цепи B0 :
Найдём величину, модуль и значение угла напряжения на участке цепи B0 :
Определим напряжение на участке цепи 0C :
Найдём величину, модуль и значение угла напряжения на участке цепи 0C :
Определим напряжение нуля относительно нейтрали 0N через напряжение ветви 0C :
Найдём величину, модуль и значение угла напряжения нуля относительно нейтрали 0N :
Определим напряжение нуля относительно нейтрали через напряжение ветви B0 :
Найдём величину, модуль и значение угла напряжения нуля относительно нейтрали B0 :
Построим в VISIO Express Drawing 2.0 векторную диаграмму напряжений со смещением нуля относительно нейтрали после обрыва линейного провода и покажем направление тока IBC :
Определим и найдём резонансную частоту f0 , учитывая, что при этой частоте выполняется равенство индуктивного и ёмкостного сопротивлений :
По формуле Томпсона определим резонансную частоту w0 :
Определим и найдём активное сопротивление на ветви B0 :
Определим и найдём активное сопротивление на ветви 0C :
Определим и найдём активное сопротивление на ветви BC через активные сопротивления RB и RC :
Определим и найдём реактивно-ёмкостное сопротивление на ветви 0C :
Определим и найдём реактивно-индуктивное сопротивление на ветви B0 :
Определим и найдём полное сопротивление на ветви B0 через активное и реактивно-индуктивное сопротивления :
Определим и найдём полное сопротивление на ветви 0C через активное и реактивно-ёмкостное сопротивления :
Определим и найдём полное сопротивление на ветви BC через активное сопротивление RBC , реактивно-ёмкостное и реактивно-индуктивное сопротивления xLB0(w) и xC0C(w) :
По закону Ома определим и найдём действующее значение тока IBC(w) :
По закону Ома определим и найдём напряжение на ветви B0 :
По закону Ома определим и найдём напряжение на ветви 0C :
Определим также величину угловой частоты w1 и укажем диапозон изменения угловой частоты w :
Построим графики и сделаем на них метки показаний приборов, полученные нами на виртуальных приборах Electronics Workbench 5.12 :
Зачётная работа по теме"Расчёт
цепей трёхфазного синусоидального
тока по схеме "Звезда"
Задание 1. Сопротивление. 1.1 Найдите модуль вектора импеданса zA0=(4+4i) Ом .
1.2 Найдите на комплексной плоскости угол между действительной осью и вектором zA0 (аргумент вектора).
1.3 Задайте zA0 в тригонометрической форме.
1.4 Задайте zA0 в экспоненциальной форме.
1.5 Представьте zA0 в форме векторной диаграммы на комплексной плоскости.
1.6 Запишите синусоидальную функцию, соответствующую zA0 .
1.7 Найдите вектор, обратный zA0 :
а) в векторной форме;
b) в экспоненциальной форме;
c) в тригонометрической форме.
1.8 Какой реактивный характер имеет нагрузка?
1.9 Определите индуктивность (ёмкость) на частоте 50 Гц.
1.10 Постройте частотную характеристику:
а) импеданса;
b) адмиттанса;
c) реактивного сопротивления.
Задание 2. Напряжение.
2.1 Постройте векторную диаграмму UA0 (см. рис.).
2.2 Получите временную диаграмму в Mathcad и
EWB.
2.3 Создайте виртуальную модель в EWB генератора трёхфазного тока ( U,f ).
2.4 Задайте в Mathcad векторы фазных напряжений:
а) UA0 -в векторной форме;
b) UB0 -в тригонометрической форме;
c) U0C -в экспоненциальной форме
(см. значения в зад.3.1).
2.5 Постройте векторную диаграмму напряжений .
2.6 Получите осциллограмму напряжений в
EWB.
2.7 Постройте график напряжений в Mathcad .
Задание 3. Токи. 3.1 Найдите IA0 , IB0 , IC0 ,если zB0=(3+5i) Ом , zC0=10 Ом по закону Ома .
3.2 Определите угол сдвига фаз между током и напряжением в каждой фазе.
3.3 Постройте графики тока и напряжения в фазе A0 в Mathcad и осциллограммы в EWB. Покажите также фазовые диаграммы.
3.4 Постройте векторную диаграмму токов и напряжений.
3.5 Найдите для тока IB0 :
а) модуль;
b) амплитуду;
с) начальную фазу.
Задание 4. Мощность. 4.1 Найдите активную мощность.
4.2 Найдите реактивную мощность.
4.3 Найдите полную мощность.
Задание 5. Резонансные кривые. 5.1 Постройте частотные характеристики в фазах A0 , B0 , C0 :
a) импеданса;
b) тока;
c) мощности.
Вариант ответа на вопросы
зачётной работы. Задание 1. Сопротивление.
1.1 Найдите модуль вектора импеданса zA0:=(7+6i) Ом .
1.2 Найдите на комплексной плоскости угол между действительной осью и вектором zA0 (аргумент вектора).
1.3 Задайте zA0 в тригонометрической форме.
1.4 Задайте zA0 в экспоненциальной форме.
1.5 Представьте zA0 в форме векторной диаграммы на комплексной плоскости.
1.6 Запишите синусоидальную функцию, соответствующую zA0 .
1.7 Найдите вектор, обратный zA0 :
а) в векторной форме;
b) в экспоненциальной форме;
c) в тригонометрической форме.
1.8 Какой реактивный характер имеет нагрузка?
Характер
нагрузки является активно-индуктивным
1.9 Определите индуктивность (ёмкость) на частоте 50 Гц.
1.10 Постройте частотную характеристику:
а) импеданса;
b) адмиттанса;
c) реактивного сопротивления.
2.1 Постройте векторную диаграмму UA0 (см. рис.).
2.2 Получите временную диаграмму в Mathcad и
EWB.
2.3 Создайте виртуальную модель в EWB генератора трёхфазного тока ( U,f ).
2.4 Задайте в Mathcad векторы фазных напряжений:
а) UA0 -в векторной форме;
b) UB0 -в тригонометрической форме;
c) U0C -в экспоненциальной форме
2.5 Постройте векторную диаграмму напряжений .
2.6 Получите осциллограмму напряжений в
EWB.
2.7 Постройте график напряжений в Mathcad .
3.1 Найдите IA0 , IB0 , IC0 ,если zB0=(3+5i) Ом , zC0=10 Ом по закону Ома .
3.2 Определите угол сдвига фаз между током и напряжением в каждой фазе.
3.3 Постройте графики тока и напряжения в фазе A0 в Mathcad и осциллограммы в EWB. Покажите также фазовые диаграммы.
3.4 Постройте векторную диаграмму токов и напряжений.
3.5 Найдите для тока IB0 :
а) модуль;
b) амплитуду;
с) начальную фазу.
4.1 Найдите активную мощность.
4.2 Найдите реактивную мощность.
4.3 Найдите полную мощность.
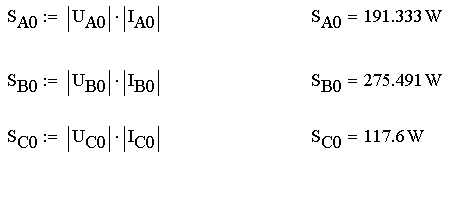 Задание 5. Резонансные кривые.
5.1 Постройте частотные характеристики в фазах A0 , B0 , C0 :
a) импеданса;
b) тока;
c) мощности.
Литература используемая в
проекте. 1. К а с а т к и н А. С., Немцов М.В. Электротехника: Учеб. пособие для вузов. - 4-е изд., перераб. - М.: Энергоатомиздат, 1983. - 440 с., ил.
2. Б е с с о н о в Л. А. Теоретические основы электротехники. Электрические цепи : Учебник .-10-е издание - М. : Гардарики , 2001.- 638 с.: ил. ISBN 5-8297-0026-3 (в пер.)
3. E dm i n i s t e r, Josef. Schaum's Outline of Theory and Problems of Electric Circuits. Second Edition./McGraw-Hill, Inc., 1995
4. Х о д я к о в И. А. Основы электротехники. Часть II. Под ред. И.П. Дешко. Учебное пособие /МГДТДиЮ, МИРЭА - М., 1998, 38с
5. " Математическое и электронное моделирование электрических цепей трехфазного синусоидального тока по схеме "звезда" в Electronics Workbench 5.12 Pro и Mathcad 2001 Pro". Творческий проект Никитиной Анастасии по предмету "Информационные и электронные технологии". 2001 г.
Содержание
Вернуться на страницу
<Методические разработки> |

