Вернуться на страницу <Методические разработки>
Содержание

Творческий проект по предмету
"Информационные и электронные технологии"

Объединение в одну цепь нескольких подобных по структуре цепей синусоидального тока одной частоты с независимыми источниками энергии широко применяется в технике. Объединяемые цепи синусоидального тока принято называть фазами, а всю объединенную систему цепей - многофазной системой. Таким образом, в электротехнике термин "фаза" применяется в двух различных смыслах: во-первых, это параметр периодического процесса, а во-вторых, - наименование составной части многофазной системы цепей синусоидального тока. Наибольшее распространение получила трехфазная система.

Трехфазная система была изобретена и разработана во всех деталях, включая трехфазные трансформатор и асинхронный двигатель, выдающимся русским инженером М.О.Доливо-Добровольским (1862-1919) в 1891 г. В настоящее время для передачи и распределения энергии в подавляющем большинстве случаев применяются трехфазные системы. Очень важным преимуществом трехфазной системы является также исключительная простота и дешевизна трехфазных асинхронных двигателей. Помимо трехфазной системы практическое значение имеет шестифазная система, например, в устройствах выпрямления переменного тока, и в некоторых устройствах автоматики двухфазная система.

Источником энергии в трехфазной системе служит трехфазный генератор. Он отличается от однофазного генератора синусоидального тока тем, что в пазах его статора размещены не одна, а три электрически изолированные друг от друга обмотки - фазные обмотки генератора. Если ротор генератора двухполюсный, то оси фазных обмоток повернуты в пространстве относительно друг друга на угол 2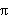/3. При вращении ротора в фазных обмотках статора индуктируются синусоидальные фазные ЭДС. Вследствие симметрии конструкции генератора максимальные Eм и действующие Еф значения ЭДС во всех фазах одинаковые. Однако линии магнитного поля вращающегося ротора пересекают провода фазных обмоток не одновременно. Поэтому синусоидальные ЭДС обмоток сдвинуты по фазе относительно друг друга на одну треть периода, чему соответствует пространственный угол 2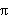/3 между осями обмоток.

Если ротор генератора многополюсный, то каждой паре его полюсов соответствуют на статоре три изолированные друг от друга катушки трехфазных обмоток. Размещение вдоль окружности статора отдельные катушки, число которых равно числу пар полюсов, каждой фазной обмотки соединяются между собой последовательно или параллельно.

Фазы трехфазного генератора принято обозначать первыми буквами латинского алфавита: А, В, С. Последовательность в обозначении фаз генератора, т.е. чередование фаз, не может быть случайной. Так как она определяется последовательностью изменений во времени фазных ЭДС. Обозначения выбираются так, чтобы ЭДС фазы А достигала максимального значения на одну треть периода раньше, чем ЭДС фазы В, и на две трети периода раньше, чем ЭДС фазы С.

Такая последовательность чередования фаз называется нормальной или прямой. От последовательности фаз зависит направление вращения трехфазных двигателей. При прямой последовательности чередования фаз мгновенные значения ЭДС трех фазных обмоток симметричного генератора равны: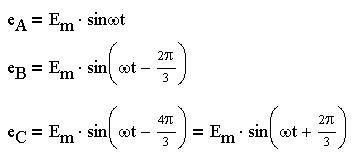

Здесь с нулевой начальной фазой, как обычно, выбрана ЭДС фазы А

Для получения трехфазной системы необходимо определенным образом соединить фазы источника энергии и фазы приемника. Возможны два основных способа соединения в трехфазной системе - соединение источника энергии и приемника по схеме звезда и соединение источника энергии и приемника по схеме треугольник.

СОЕДИНЕНИЕ ИСТОЧНИКА ЭНЕРГИИ И ПРИЕМНИКА ПО СХЕМЕ ТРЕУГОЛЬНИК

У трехфазной системы, выполненной по схеме треугольник (условное обозначение 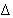), нейтральный провод отсутствует. Покажем сначала, как можно получить такую трехфазную цепь из необъединенной системы, в которой три фазные обмотки генератора соединены шестью проводами с тремя приемниками. Для получения из фазных обмоток генератора схемы треугольник соединим конец Х первой обмотки с началом В второй обмотки, конец Y второй обмотки с началом С третьей обмотки и конец Z третьей обмотки с началом А первой обмотки. Так как алгебраическая сумма синусоидальных фаз ЭДС генератора равна нулю, то никакого дополнительного (уравнительного) тока в обмотках генератора не возникнет. После объединения обмоток генератора напряжения между началом и концом каждой фазы не изменятся, т.е. эти фазные напряжения одинаковы для несвязанной и связанной систем. Поэтому и токи в фазах приемника, т.е. фазные токи, IАВ, IВС, IСА в связанной системе такие же, как в несвязанной. Токи в каждом из трех объединенных линейных проводов, т.е. линейные токи, равны разностям соответствующих фазных токов (первый закон Кирхгофа для узлов приемника):

IА = IАВ - IСА
IB = IВC - IАB
IC = ICA - IBC

 Линейные напряжения равны соответствующим фазным напряжением, их комплексные значения: 

UАВ = EА; UВС = EВ; UСА = EС

По закону Ома комплексные значения фазных токов:  

IАВ = EА/ ZAB; IВC = EB/ZBC; ICA = EA/ZCA

У всех фазных токов одинаковые действующие значения Iф и одинаковые сдвиги фаз 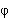относительно соответствующих ЭДС или фазных напряжений.

Преимуществом соединения источника энергии и приемника по схеме треугольник по сравнению с соединением по схеме звезда без нейтрального провода является взаимная независимость фазных токов. Если при таком соединении перегорит один из магистральных предохранителей, то лампы в двух фазах окажутся последовательно включенными и при одинаковой мощности ламп напряжение на лампах каждой из этих фаз будет равно только половине линейного напряжения; напряжение на лампах третьей фазы останется нормальным.

АКТИВНАЯ, РЕАКТИВНАЯ И ПОЛНАЯ МОЩНОСТИ ТРЕХФАЗНОЙ СИММЕТРИЧНОЙ СИСТЕМЫ.

Активной мощностью трехфазной системы называется сумма активных мощностей всех фаз источника энергии, равная сумме активных мощностей всех фаз приемника.

В симметричной трехфазной системе, т.е. системе с симметричными генератором и приемником, при любой схеме их соединений для каждой фазы мощности источника энергии приемника одинаковые. В этом случае P=3Pф и для каждой из фаз справедлива формула активной мощности синусоидального тока:

Pф = Uф Iф cos,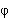

где 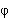- угол сдвига фаз между фазными напряжением и током.

В общем случае реактивной мощностью трехфазной системы называется сумма реактивной мощности всех фаз источника энергии, равная сумме реактивных мощностей всех фаз приемника. Реактивная мощность симметрична трехфазной системе по

Q = 3Qф =3Uф Iф sin,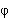

или после замены действующих значений фазных тока и напряжения линейными.

Q = v3 Uл Iл sin.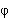

Комплексной мощностью трехфазной системы называется сумма комплексных мощностей фаз источника энергии, равная сумме комплексных мощностей всех фаз приемника.

Полная мощность симметричной трехфазной системы

S = v3 Uл Iл .

МОДЕЛЬ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПО СХЕМЕ "ТРЕУГОЛЬНИК".

У трёхфазной системы, выполненной по схеме треугольник, нейтральный провод отсутствует. Преимуществом соединения источника энергии и приемника по схеме треугольник, по сравнению с соединением по схеме звезда, без нейтрального провода, является взаимная независимость фазных токов.

Если при таком соединении в осветительной установке перегорит один из магистральных предохранителей, то лампы в двух фазах окажутся последовательно включёнными, и при одинаковой мощности ламп напряжение на лампах каждой из этих фаз будет равно только половине линейного (номинального) напряжения; напряжение на лампах третьей фазы останется нормальным.

Для расчета цепи определим линейные напряжения UAB, UBC, UCA, частоту, угловую частоту и период и найдем их значения:

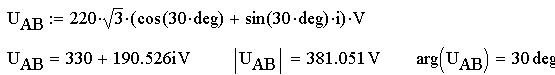
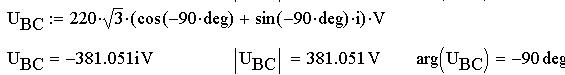
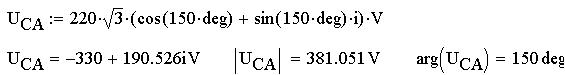
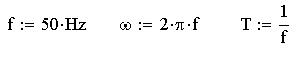
Также определим индуктивность, емкость и сопротивление для каждой ветви:

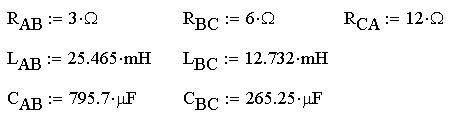
Создадим в Electronics Workbench 5.12 виртуальную модель трехфазной электрической цепи:

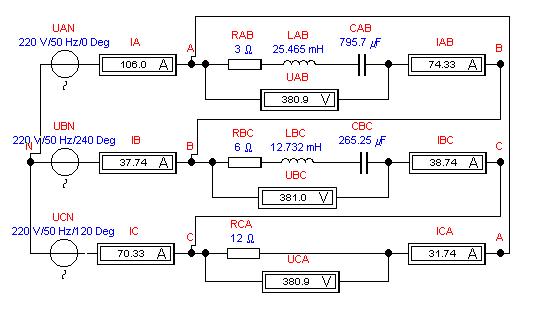
Теперь определим и вычислим индуктивное, емкостное и полное сопротивления для ветвей:

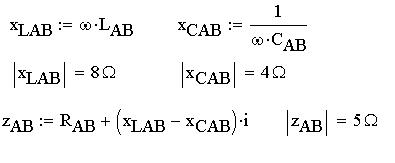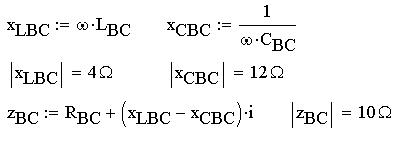
По закону Ома определим и вычислим фазные токи IAB, IBC и ICA:

Определим линейные токи через фазные и вычислим их:

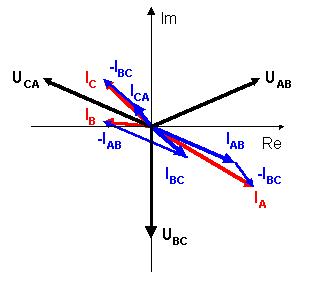
Создадим в Visio Express Drawing 3.0 векторную диаграмму токов:

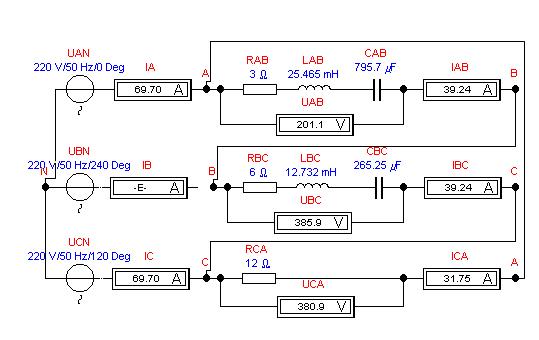
ОБРЫВ ЛИНЕЙНОГО ПРОВОДА В.

Рассмотрим в Electronics Workbench 5.12 электронную модель и определим показания приборов в MathCAD 2001, показав их на резонансных кривых участков цепи.

Найдем теперь значения для образовавшейся фазы СВА, полученной из последовательно включенных фазных цепей АВ и ВС, включенной под линейное напряжение UCA параллельно фазе СА.

По закону Ома посчитаем действующее значение силы тока, а также полное сопротивление в фазе СВА:

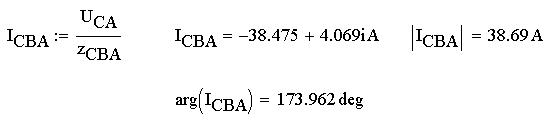
Так как токи в линейных проводах А и С равны, то найдем их значение:

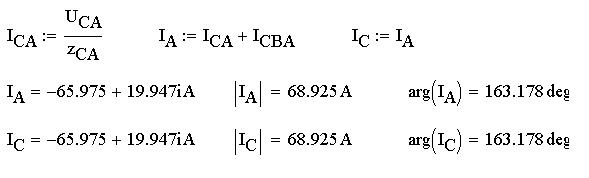
Определим значения напряжений на участках АВ и ВС:

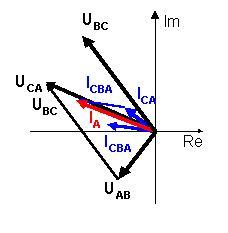
Создадим в Visio Express Drawing 3.0 векторную диаграмму токов и напряжений:

НАХОЖДЕНИЕ ПОКАЗАНИЙ ПРИБОРОВ ПО РЕЗОНАНСНЫМ КРИВЫМ НА УЧАСТКАХ АВ И ВС ФАЗЫ СВА.

Определим величины частоты, угловой частоты 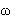1, соответствующей рабочей частоте и диапазон изменения угловой частоты, а также значения линейного напряжения СА:

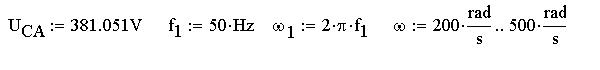
Найдем индуктивные и емкостные сопротивления на участках АВ и ВС:

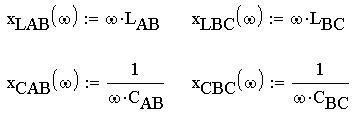
Найдем индуктивные и емкостные сопротивления на участках АВ и ВС:

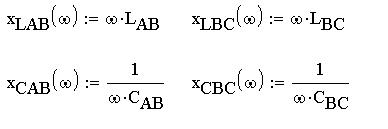
Посчитаем суммарное активное и реактивные сопротивления фазы CBA, полные сопротивления участков AB и BC, а также всей фазы CBA как функции угловой частоты на участках АВ и ВС:

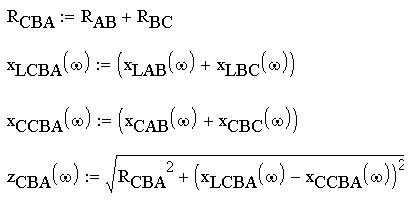
Вычислим резонансную частоту фазы CBA из условия, что на этой частоте выполняется равенство величин индуктивного и емкостного сопротивлений, откуда следует формула Томсона для резонансной частоты w0:

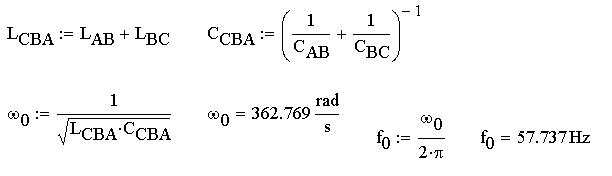
Найдем величину полного сопротивления фазы CBA на рабочей частоте и отметим её риской на графике частотной зависимости полного сопротивления:

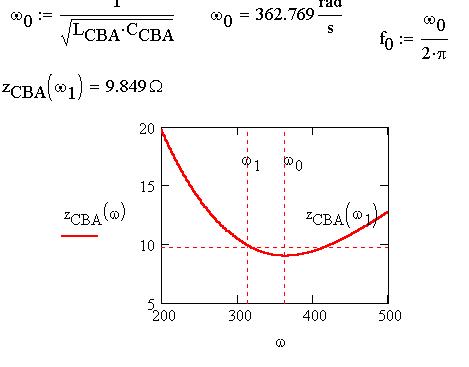
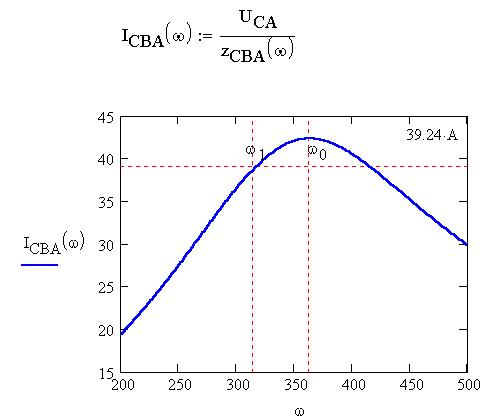
Построим частотную характеристику силы тока в фазе CBA, найденной по закону Ома, и отметим на ней риской показание амперметра из электронной модели, созданной в Electronics Workbench 5.12:

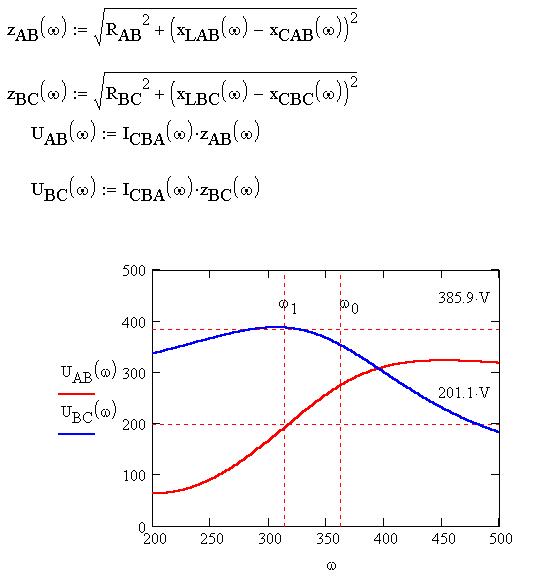
Определим по закону Ома частотные характеристики напряжений на участках AB и BC фазы CBA и отметим на графиках этих характеристик показания вольтметров из электронной модели:

ЛИТЕРАТУРА:

1. Пискунов Н.С. "Дифференциальное и интегральное исчисления." Издательство "Наука". Москва 1965.
2. Бронштейн И.Н. и Семендяев К.А. "Справочник по математике." Москва "Наука" 1986.
3. Панфилов Д.И. "Электротехника и электроника в экспериментах и упражнениях." Издательство "Додэка" Москва 1999.
4. Ходяков И.А. "Основы электротехники." 1998
5. Калашников С. Г. Электричество. Издательство "Наука". - М., 1970
6. Сборник творческих проектов учащихся 1998/99.

Содержание
Вернуться на страницу <Методические разработки>