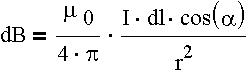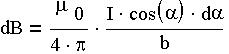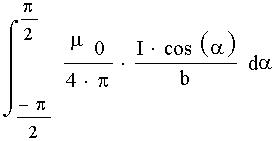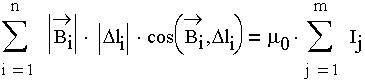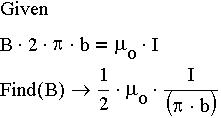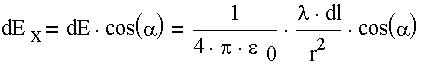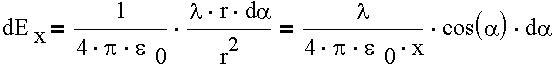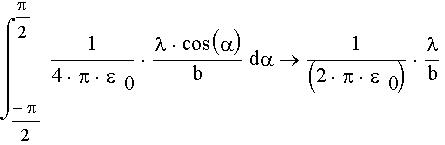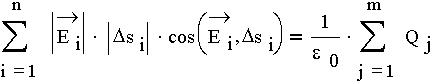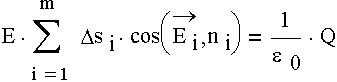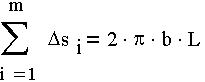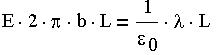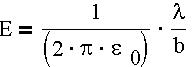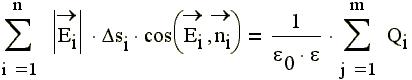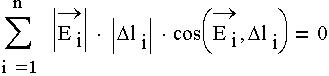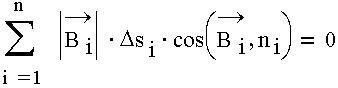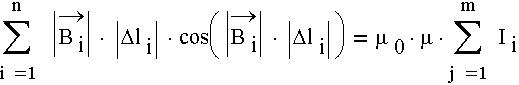| Купить Matlab | Mathematica | Mathcad | Maple | Statistica | Другие пакеты |  |
| Internet-класс | Примеры | Методики | Форум | Download | |
|
|
Содержание.
История математики."Под наукой чисел понимаются две
науки: Аль-Фараби Зачатки счета теряются в глубине веков и относятся к тому периоду истории человечества, когда еще не было письменности. Писать человек научился тогда, когда он довольно далеко продвинулся в умении считать. Математические знания в далеком прошлом применялись для решения повседневных задач, и именно практика в значительной степени руководила всем дальнейшим развитием математики. Последние три столетия дали науке ряд блестящих математических результатов: решены три классические задачи древности, над которыми трудились ученые в течение четырех тысячелетий, - квадратура круга, трисекция угла и удвоение куба, построены новые математические науки, позволившие открыть неизвестные ранее объекты математического познания; достигнута огромная гибкость математических понятий и методов исследования, способных охватить все многообразие проблем естествознания, технических и социальных дисциплин. Геометрия.Аксиома. "Так называемые аксиомы Ф.Энгельс Начальные геометрические сведения дошли до нас из глубокой древности. Например, формулы для вычисления площадей земельных участков, имеющих форму прямоугольника, треугольника, трапеции, приведены в древнеегипетских математических папирусах, относящихся к 2000 г. до н. э., в клинописных таблицах Древнего Вавилона. Начальные геометрические знания были добыты опытным путем. Получение новых геометрических фактов при помощи рассуждений (доказательств) началось от древнегреческого ученого Фалеса (VI в. до н. э.). Постепенно доказательства приобретают в геометрии все большее значение. К III в. до н. э. геометрия становится дедуктивной наукой, т. е. наукой, в которой большинство фактов устанавливается путем вывода (дедукции), доказательства. К этому времени относится книга "Начала", написанная древнегреческим ученым Евклидом. В ней доказываются свойства параллелограммов и трапеций, приведена теорема Пифагора, изучается подобие многоугольников, рассматриваются многие другие геометрические факты. Некоторые факты настолько просты, что не возникает вопроса о необходимости их вывода. Их назвали аксиомами (это греческое слово означает "удостоенное, принятое положение"). Весь набор аксиом (система) называется аксиоматикой. Таким образом, аксиомы - это первоначальные факты геометрии, которые принимаются без доказательства и позволяют вывести из них все дальнейшие факты этой науки. Утверждения, выводимые из аксиом, называют теоремами. Среди сформулированных Евклидом аксиом имеются, например, следующие: "через две точки можно провести прямую"; "порознь равные третьему равны между собой"; "если в плоскости даны прямая и лежащая вне этой прямой точка, то через эту точку можно провести в плоскости не более одной прямой, которая не пересекается с данной" (последняя из этих аксиом - аксиома параллельности - у Евклида формулировалась иначе). После Евклида математики многих поколений стремились улучшить, дополнить его аксиоматику геометрии. Большую роль сыграли работы Архимеда, который сформулировал аксиомы, относящиеся к измерению геометрических величин. Из ученых более позднего времени существенный вклад в усовершенствование аксиоматики внесли русский математик Н. И. Лобачевский, французский математик М. Паш, итальянский математик Дж. Пеано. Логически безупречный список аксиом геометрии был указан на рубеже XIX и XX вв. немецким математиком Д. Гильбертом. Алгебра."Алгебра есть не что иное, И. Ньютон Алгебра - часть математики, которая изучает общие свойства действий над различными величинами и решение уравнений, связанных с этими действиями. Решим задачу: "Возрасты трех братьев - 30, 20 и 6
лет. Через сколько лет возраст старшего будет
равен сумме возрастов обоих младших братьев?"
Обозначив искомое число через x, составим
уравнение: Еще более сложные задачи умели решать с начала II тысячелетия до н. э. в Древнем Вавилоне: в математических текстах, выполненных клинописью на глиняных пластинках, есть квадратные и биквадратные уравнения, системы уравнений с двумя неизвестными и даже простейшие кубические уравнения. При этом вавилоняне также не использовали букв, а приводили решения "типовых" задач, из которых решения аналогичных задач получались заменой числовых данных. В числовой же форме приводились и некоторые правила тождественных преобразований. Если при решении уравнения надо было извлекать квадратный корень из числа а, не являющегося точным квадратом, находили приближенное значение корня х: делили а на х и брали среднее арифметическое чисел х и а/х. Первые общие утверждения о тождественных преобразованиях встречаются у древнегреческих математиков начиная с VI в. до н. э. Среди математиков Древней Греции было принято выражать все алгебраические утверждения в геометрической форме. Вместо сложения чисел говорили о сложении отрезков, произведение двух чисел истолковывали как площадь прямоугольника, а произведение трех чисел - как объем прямоугольного параллелепипеда. Алгебраические формулы принимали вид соотношений между площадями и объемами. Например, говорили, что площадь квадрата, построенного на сумме двух отрезков, равна сумме площадей квадратов, построенных на этих отрезках, увеличенной на удвоенную площадь прямоугольника, построенного на этих отрезках. С того времени и идут термины "квадрат числа", "куб числа", "среднее геометрическое". Геометрическую форму приняло у греков и решение квадратных уравнений - они искали стороны прямоугольника по заданным периметру и площади. Большинство задач решалось в Древней Греции
путем построений циркулем и линейкой. Но не все
задачи поддавались такому решению. Например,
"не решались" задачи удвоения куба,
трисекции угла, задачи построения правильного
семиугольника. Они приводили к кубическим
уравнениям вида соответственно. Для решения этих задач был разработан новый метод, связанный с отысканием точек пересечения конических сечений (эллипса, параболы и гиперболы). Геометрический подход к алгебраическим проблемам сковывал дальнейшее развитие науки, так как, например, нельзя было складывать величины разных размерностей (длины и площади или площади и объемы). Нельзя было говорить о произведении более чем трех множителей и т. д. Отказ от геометрической трактовки наметился у Диофанта Александрийского, жившего в III в. В его книге "Арифметика" появляются зачатки буквенной символики и специальные обозначения для степеней неизвестного вплоть до шестой. Были у него и обозначения для степеней с отрицательными показателями, обозначения для отрицательных чисел, а также знак равенства (особого знака для сложения еще не было), краткая запись правил умножения положительных и отрицательных чисел. На дальнейшее развитие алгебры сильное влияние оказали разобранные Диофантом задачи, приводящие к сложным системам алгебраических уравнений, в том числе к системам, где число уравнений было меньше числа неизвестных. Для таких уравнений Диофант искал лишь положительные рациональные решения. С VI в. центр математических исследований перемещается в Индию и Китай, страны Ближнего Востока и Средней Азии. Китайские ученые разработали метод последовательного исключения неизвестных для решения систем линейных уравнений, дали новые методы приближенного решения уравнений высших степеней. Индийские математики использовали отрицательные числа и усовершенствовали буквенную символику. Однако лишь в трудах ученых Ближнего Востока и Средней Азии алгебра оформилась в самостоятельную ветвь математики, трактующую вопросы, связанные с решением уравнений. В IX в. узбекский математик и астроном Мухаммед Аль Хорезми написал трактат "Китаб аль-джебр валь-мукабала", где дал общие правила для решения уравнений первой степени. Слово "аль-джебр" (восстановление), от которого новая наука алгебра получила свое название, означало перенос отрицательных членов уравнения из одной его части в другую с изменением знака. Ученые Востока изучали и решение кубических уравнений, хотя не сумели получить общей формулы для их корней. В Западной Европе изучение алгебры началось в XIII в. Одним из крупных математиков этого времени был итальянец Леонардо Пизанский (Фибоначчи). Его "Книга абака" (1202) - трактат, который содержал сведения об арифметике и алгебре до квадратных уравнений включительно. Первым крупным самостоятельным достижением западноевропейских ученых было открытие в XVI в. формулы для решения кубического уравнения. Это было заслугой итальянских алгебраистов С. дель Ферро, Н. Тартальи и Дж. Кардано. Ученик последнего - Л. Феррари решил и уравнение четвертой степени. Изучение некоторых вопросов, связанных с корнями кубических уравнений, привело итальянского алгебраиста Р. Бомбелли к открытию комплексных чисел. Отсутствие удобной и хорошо развитой символики сковывало дальнейшее развитие алгебры: самые сложные формулы приходилось излагать в словесной форме. В конце XVI в. французский математик Ф. Виет ввел буквенные обозначения не только для неизвестных, но и для произвольных постоянных. Символика Виета была усовершенствована многими учеными. Окончательный вид ей придал в начале XVII в. французский философ и математик Р. Декарт, который ввел (употребляемые и поныне) обозначения для показателей степеней. Развитие буквенной символики позволило установить общие утверждения, касающиеся алгебраических уравнений: теорему Безу о делимости многочлена P(x) на двучлен (x-a), где а - корень этого многочлена; соотношения Виета между корнями уравнения и его коэффициентами; правила, позволяющие оценивать число действительных корней уравнения; общие методы исключения неизвестных из систем уравнений. Особенно далеко было продвинуто в XVIII в. решение систем линейных уравнений - для них были получены формулы, позволяющие выразить решения через коэффициенты и свободные члены. Дальнейшее изучение таких систем уравнений привело к созданию теории матриц и определителей. В конце XVIII в. было доказано, что любое алгебраическое уравнение с комплексными коэффициентами имеет хотя бы один комплексный корень. Это утверждение носит название основной теоремы алгебры. После создания теории комплексных чисел возник
вопрос о существовании гиперкомплексных чисел -
чисел с несколькими "мнимыми единицами".
Такую систему чисел, имевших вид Таким образом, в течение XIX в. в математике возникли разные виды алгебр: обычных чисел, комплексных чисел, кватернионов, матриц, высказываний, множеств и т. д. Каждая из них имела свои правила, свои тождества, свои методы решения уравнений. Дифференциальное исчисление.Дифференциальное исчисление (вместе с интегральным) появилось в XVII веке; рассмотренное вначале в частных случаях многими учеными в геометрическом и кинематическом аспекте (Ферма, Торричелли, Ролль, Барроу), оно было сформулировано общим образом в конце века И. Ньютоном и Г. Лейбницем. Лейбниц ввел символ дифференциала и обозначение для производной. Ньютон, затем Лейбниц и его ученики, в первую очередь братья Якоби и Иоганн Бернулли, применили методы дифференциального исчисления к многочисленным проблемам геометрии, механики и физики. Интегральное исчисление.Алгоритмы дифференциального исчисления, их основные понятия были созданы независимо друг от друга И. Ньютоном и Г. Лейбницем. Применяя открытую им общую теорему о степени бинома, И. Ньютон выражал интегралы через бесконечные степенные ряды. Таким образом были проинтегрированы многие иррациональные функции. Интегрирование в конечном виде также не было оставлено И. Ньютоном без внимания, хотя играло в его исследованиях второстепенную роль. Так в 1676 году он указал, что интеграл дифференциального бинома выражается через алгебраические функции. Применяя замену переменных и некоторые другие приёмы, И. Ньютон установил ряд. Случаев интегрируемости в алгебраических, логарифмических и обратных тригонометрических функциях интегралов, причем последние два вида функций фигурировали у него в форме величин площадей некоторых конических сечений, а аналитически могли быть выражены в общем случае с помощью бесконечных рядов. В "математических анализах натуральной философии" (1687) И. Ньютон фактически приводил вычисления, равносильные вычислению некоторых двойных и тройных интегралов, но соответствующие общие понятия были введены позднее. Понятие интеграла у Г. Лейбница выступило, наоборот, прежде всего в форме определенного интеграла, в виде суммы бесконечного числа бесконечно малых дифференциалов, на которые разбита та или иная величина. Введение понятия интеграла и его обозначений относится к осени 1675. Знак интеграла был опубликован в статье Г. Лейбница 1686; термин "интеграл" впервые в печать употребил Я. Бернулли в 1690. вычисление интегралов Г. Лейбниц и его ученики, первыми из которых явились братья Я. и И. Бернулли, сводили к обращению операции дифференцирования, т. е. К отысканию первообразных. При вычислении интегралов с определенными пределами с помощью неопределенных интегралов как и И. Ньютон, так и Г. Лейбниц пользовались носящей их имя формулой; однако современная терминология была создана только в конце XVIII века. Среди употреблявшихся Г. Лейбницем специальных способов интегрирования были: замена переменной, интегрирование по частям, а также дифференцирование по параметру под знаком интеграла (1697). Г. Лейбницу же принадлежит идея интегрирования рациональных дробей при помощи разложения на простейшие дроби (1702-1703), впоследствии усовершенствования другими учеными. К И. Ньютону и Г. Лейбницу и некоторым их современникам восходит также применение методов графического интегрирования. Истоки современной электротехники.Истоки современной электротехники восходят к замечательным трудам английского ученого Майкла Фарадея, которые, в свою очередь, были подготовлены предшествовавшими работами по изучению электрических и магнитных явлений. Жизнь великого ученого и его неповторимая по своим методам, содержанию и значению деятельность не только открыли новую главу физики, но сыграли решающую роль в рождении новых отраслей в технике: электротехники и радиотехники. Фарадей был признанным "королем экспериментаторов". Работам Фарадея в области электричества положило начало исследование так называемых электромагнитных вращений. Из серии опытов Эрстеда, Арго, Ампера, Био, Савара, проведенных в 1820 году стало известно не только об электромагнетизме, но и о своеобразии взаимодействий тока и магнита. Максвеллом был разработан метод контурных токов, доказана теорема взаимности. Постепенно формировался практически весь арсенал методов расчета цепей постоянного тока. После открытия электромагнитной индукции внимание ученых в значительной степени переключилось с "гальванических" токов, когда главными объектами исследований были сами гальванические элементы, процессы электролиза, на индукционные токи, когда наибольший интерес стали вызывать явление электромагнетизма. Здесь особая роль принадлежит выдающемуся русскому физику Э.Х. Ленцу. В своем докладе Петербургской Академии наук 29 ноября 1833 года Э.Х. Ленц, находясь под большим впечатлением от работ по электромагнитной индукции М. Фарадея, дал свою замечательную формулировку закона, названного его именем. Ленц был одним из основоположников теории магнитоэлектрических машин. Заслуга Максвелла состоит в том, что, использовав накопленный до него громадный экспериментальный материал, он обобщил и развил прогрессивные идеи Фарадея, придав им стройную математическую форму. Важнейшие результаты своих исследований Максвелл сформулировал в виде знаменитых уравнений, получивших его имя. Максвелл обобщил закон электромагнитной индукции, распространив его на произвольный контур в любой среде. Максвелл не дожил до торжества своих глубоких научных идей и обобщений. Количественные соотношения иногда только угадываются за качественными рассуждениями, как это было характерно для все исследований Фарадея. До 80-х годов ХIX В работах Гельмгольца, Максвелла, У.Томсона (лорда Кельвина), Ф.Неймана и других физиков появляются строгие математические связи между мгновенными значениями токов и напряжений, появляются основные уравнения цепей в дифференциальной форме. В 80-е гг. делаются попытки сравнивать действия постоянного и переменного токов, вводится понятие об идеальном синусоидальном токе. В1888 году У. Томсон показал возможность применения гармонического анализа Фурье для любого периодического тока. Наибольших успехов в развитии многофазных систем добился М.О. Доливо-Добровольский, который сумел придать своим работам практический характер. Поэтому он по праву считается основоположником техники трехфазных систем. В XVIII веке в механику проникают методы дифференциального и интегрального исчисления, и она становится аналитической. Огромная заслуга в развитии механики принадлежала петербургскому академику Леонарду Эйлеру (1707-1703) и парижскому академику Жозефу Луи Лагранжу (1736-1813). Эйлер переформулировал основные понятия ньютоновской механики, придав им соответственную форму, но сохранив сущность по Ньютону. Именно Эйлер впервые записал второй закон динамики в аналитической форме, сделав его основным законом всей механики. XVIII век в области механики характеризуется также поиском более общих принципов, чем законы Ньютона. В этот период создается теоретическая механика. Наибольший вклад в ее развитие внес Лагранж. Открытия сделанные Фарадеем в области электромагнетизма, находили все большее и большее использование. Однако его концепция силовых линий, занимающих все пространство, долгое время не принимали всерьез: она не смогла конкурировать со стройными теориями Кулона, Ампера, Лапласа. Не владея хорошо математическим методом, Фарадей не стремился привязать его к своим исследованиям. Он считал, что самые сложные вопросы можно изложить просто, не прибегая к "языку иероглифов". Это был "ум, который никогда не погрязал в формулах",- скажет о нем Эйнштейн. Вот почему молодой Максвелл, взявшись за "атаку электричества", имел все основания заявить: "Современное состояние учения об электричестве представляется особенно неблагоприятным для теоретической разработки". В это время Максвеллу было 24 года. Приложение I (биографическая справка)Ньютон Исаак. (Newton I.)(4.I. 1643-31.III. 1727) Выдающийся английский ученый, заложивший основу современного естествознания, создатель классической физики, член Лондонского королевского общества (1672), президент (с 1703). Родился в Вулсторпе. С 12 лет учился в школе в Грантеме. С1661 по 1665 учился в Кембриджском университете. В 1668 году получил степень магистра. В 1669-1701 возглавил в нем кафедру. В 1695 был назначен смотрителем, с 1699- главный директор монетного двора в Лондоне. Похоронен в английском национальном пантеоне - Вестминстерском аббатстве. Работы относятся к механике, оптике, астрономии, математике. Сформулировал основные законы классической механики, открыл закон всемирного тяготения, дисперсию света, развил корпускулярную теорию света, разработал (независимо от Г. Лейбница) дифференциальное и интегральное исчисление. Обобщив результаты исследований своих предшественников в области механики и свои собственные, создал огромный труд "Математические начала натуральной философии" ("Начала"), изданий в 1687. "Начала" содержали основные понятия и аксиоматику классической механики, в частности понятия масса (которому Ньютон придавал большое значение как основному в механических процессах), количество движения, сила, ускорение, центростремительная сила и три закона движения (законы Ньютона) - закон инерции, закон пропорциональности силы ускорению и закон действия и противодействия. Тут же дан его закон всемирного тяготения, исходя из которого Ньютон объяснил движение небесных тел (планет, их спутников, комет), и создал теорию тяготения. Открытие этого закона знаменовало переход от кинематического описания солнечной системы к динамическому объяснению явлений и окончательно утвердило победу учения Коперника. Он показал, что из закона всемирного тяготения вытекают три закона Кеплера; объяснил особенности движения луны, явление процессии; развил теорию фигуры Земли, отметив, что она должна быть сжата у полюсов, теорию приливов и отливов; рассмотрел проблему создания искусственного спутника Земли и т. д. Установил закон сопротивления и основной закон внутреннего трения в жидкостях и газах, дал формулу для скорости распространения волн. Создал физическую карту мира, которая длительное время господствовала в науке (ньютоновская теория пространства и времени). Пространство и время он считал абсолютными, постулируя это в своих "Началах". С таким пониманием пространства и времени тесно связана его идея дальнодействия - мгновенной передачи действия одного тела к другому на расстоянии через пустое пространство без помощи материи. Ньютоновская теория дальнодействия и его схема мира господствовали до начала XХ века. Впервые её ограниченность обнаружили М. Фарадей и Дж. Максвелл, неприменимость её к электромагнитным явлениям, а теория относительности, возникшая в начале ХХ века, окончательно доказала ограниченность классической физики Ньютона - физики малых скоростей и макроскопических масштабов. Однако специальная теория относительности не отбросила совсем закономерностей, установленных классической механикой Ньютона, а лишь уточнила и дополнила её для случая движения со скоростями, соизмеримыми со скоростью света в вакууме. "Ныне место ньютоновской схеме дальнодействующих сил, - написал А. Эйнштейн, - заняла теория поля, испытали изменения и его законы, но всё, что было создано после Ньютона, является дальнейшим органическим развитием его идеи и методов". Велик вклад Ньютона в оптику. В 1666 году при помощи трехгранной стеклянной призмы разложил белый свет на семь цветов (в сектор), тем самым доказав его сложность (явление дисперсии), открыл хроматическую аберрацию. Пытаясь избежать аберрации в телескопах, в 1668 и в 1671 сконструировал телескоп-рефлектрор оригинальной системы - зеркальный (отражательный), где вместо линзы использовалось вогнутое сферическое зеркало (телескоп Ньютона). Исследовал интерференцию и дифракцию света, изучая цвета тонких пластинок, открыл так называемые кольца Ньютона, установил закономерности в их размещении, высказал мысль о периодичности светового процесса. Пытался объяснить двойное лучепреломление и близко подошёл к открытию явления поляризации. Свет считал потоком корпускул - корпускулярная теория света Ньютона (однако на разных этапах рассматривал возможность существования и волновых свойств света, в частности в 1675 году предпринял попытку создать компромиссную). Свои оптические исследования изложил в "Оптике" (1704). По своему мировоззрению Ньютон был стихийным материалистом, вторым после Р. Декарта великим представителем механического материализма в естествознании XVII - XVIII веках. Научное творчество Ньютона сыграло исключительно важную роль в истории развития физики. По словам А. Эйнштейна, "Ньютон был первым, кто попытался сформулировать элементарные законы, которые определяют временной ход широкого класса процессов в природе с высокой степенью полноты и точности" и "… оказал своими трудами глубокое и сильное влияние на все мировоззрения в целом". В его честь названа единица силы в
Международной системе единиц - ньютон. Уже в 1665-1666
годах он для нужд выработал основные идеи этого
метода, исходя преимущественно из работ Б.
Кавальери, Ж. Роберваля, П. Ферма, Д. Валлиса и
своего учителя И. Барроу. На это время приходится
и его открытие взаимно обратного характера
операций дифференцирования и интегрирования, а
так же фундаментальные открытия в области
бесконечных рядов, в частности индуктивное
обобщение так называемые теоремы о биноме
Ньютона на случай любого действительного
показателя. Уже в первой работе по анализу
("Анализ с помощью уравнений с бесконечным
числом членов"), написанной в 1669 году, а
опубликованной только в 1711 году, ученый дал метод
вычислений и изучения функций - приближение
бесконечными рядами, который имел впоследствии
огромное значение для всего анализа. На этой
основе Ньютон почленным интегрированием получил
ряды для Лейбниц Готфрид Вильгельм (Leibniz G.)(1.VII.1646 - 14.XI.1716) Немецкий математик, физик, философ, организатор и первый президент Берлинской АН (1700); член Лондонского королевского общества (1673 год), член Парижской АН (1700). Родился в Лейпциге. В 1661 году Лейбниц поступил на юридический факультет Лейпцигского университета. Кроме юридических наук изучал философию и математику. В университете ознакомился с работами Аристотеля и Р. Декорта. Защитил диссертацию на степень бакалавра (1663), магистра философии(1664) и доктора права (1666). Состоял на юридической и дипломатической службе при дворе Майнцкого курфюрста. Из Майнца он выезжал с дипломатической миссией в Париж. Творческая деятельность Лейбница развернулась именно в тот период в Париже, где он много работал и лично познакомился со многими математиками, в частности с Х. Гюйгенсом, под руководством которого изучал работы Г. Галилея, Р. Декарта, П. Ферма, Б. Паскаля и самого Гюйгенса. В 1673 году из Парижа Лейбниц выезжает в Лондон для демонстрации своей счетной машины в королевском обществе. Там он познакомился с И. Борроу, а также с трудами И. Ньютона, "Логарифмотехникой" Г. Меркатора. Возвратясь в 1676 году в Париж, Лейбниц разрабатывает важные вопросы дифференциального исчисления. В том же году Лейбниц уезжает в Ганновер, где работает сначала библиотекарем, а потом историографом двора Ганноверского герцога. Однако деятельность Лейбница выходила далеко за пределы официальных обязанностей. Он занимается и вопросами химии, геологии, конструирует ветряной двигатель для насосов, выкачивающих воду из шахт. Особенно плодотворной была научная деятельность Лейбница в области математики. В 1666 году он опубликовал свою первую математическую работу "Размышления о комбинаторном искусстве". Сконструированная им счетная машина выполняла не только сложение и вычитание, как это было у Б. Паскаля, но и умножение, деление, возведение в степень и извлечение квадратного и кубического корней. Свыше 40 лет Лейбниц посвятил усовершенствованию своего изобретения. Именно по этому его можно считать идейным вдохновителем современной машинной математики. Лейбниц заложил основы символической логики. Исследовал свойства некоторых кривых (в частности, цепной линии), разложение функции в ряды, ввел понятие определителя и выдвинул некоторые идеи, касающиеся теории определителей, которые впоследствии развивали А. Вандермонд, О. Коши, К. Гаусс и окончательно разработал К. Якоби. Лейбниц до некоторой степени продолжил путь таким новым дисциплинам, как политическая экономия и сравнительное языковедение. Но важнейшей его заслугой является то, что он, одновременно с Ньютоном, но независимо от него, завершил создание дифференциального и интегрального исчисления. При этом он исходил не из квадратуры кривых, как Ньютон, а из проблемы касательных. Изучение работ Б. Паскаля и собственные
исследования привели Лейбница в 1673-1674 годах к
идее характеристического треугольника, который
теперь используется при введении понятий
производной и дифференциала в каждом учебнике
дифференциального исчисления. В это время
Лейбниц осуществил и дальнейший шаг в создании
нового исчисления - установил зависимость между
прямой и обратной задачами о касательных. Через
год он пришел к выводу, что "из обратного
метода касательных выходит квадратура всех
фигур". В октябре 1675 года Лейбниц уже
пользуется обозначением Sl для суммы бесконечно
малых и операцию, противоположную суммированию,
обозначает, подписывая букву d под переменной Лейбниц ввел много математических терминов, которые теперь прочно вошли в научную практику: функция, дифференциал, дифференциальное уравнение, дифференциальное исчисление, алгоритм, абсцисса, ордината, координата, а также знаки дифференциала, интеграла, логическую символику и так далее. С именем Лейбница в науке связано много открытий и гипотез, которые позже получили признания. В механике ему принадлежит понятие о "живых силах", в геологии - мысль, что Земля имеет историю. Он также высказал правильное предположение о происхождении ископаемых остатков животных и растений, отстаивая важную для биологии мысль об эволюции. Лейбниц создал соответственную школу, в которую входили братья Бернулли, Г. Ф. Лопиталь и другие математики. Он первым нарушил и вековую традицию писать научные труды только на латинском языке. Кулон Шарль Огюстен (Coulomb Sh.)(14.VI 1736 - 23.VIII 1806) Французский физик и военный инженер, член Парижской АН (1803). Родился в Ангулеме. Окончил в 1761 году школу военных инженеров и все время находился на военной службе. Работы относятся к электричеству, магнетизму, прикладной механике. Сформулировал в 1781 году законы трения, качения и скольжения. Исследуя кручение шелковых и металлических нитей, установил законы упругого кручения, в частности определил, что сила закручивания нити зависит от материала, из которого она сделана, пропорциональна углу закручивания и четвертой степени диаметра нити и обратно пропорциональна ее длине. Это имело важное значение, поскольку давало новый, очень чувствительный метод измерения силы. Исходя из этого, в 1784 году построил прибор для измерения силы - крутильные весы. С его помощью экспериментально установил в 1785 году основной закон электростатики (закон Кулона), распространив его в 1788 году на взаимодействие точечных магнитных полюсов. Выдвинул гипотезу магнетизма, согласно которой магнитные жидкости не свободны или не могут течь, как их электрические аналоги, и связаны с отдельными молекулами. Предположил, что каждая молекула в процессе намагничивания становится поляризованной. Сконструировал в 1785 году магнитометр. Заложил основы электро-и магнитостатики. В1796 году пытался экспериментально измерить трение в жидкости по затуханию колебаний движущегося в ней маятника и определить зависимость трения от скорости. Лаплас Пьер Симон (Laplace P.)(28.III 1749 - 5.III 1827) Французский астроном, физик и математик, член Парижской АН (1785). Родился в Бомон-ан-Оже. Учился в школе бенедиктинцев. В 1771 стал профессором Военной школы в Париже, в 1790 - председателем Палаты мер и весов. Активно участвовал в реорганизации системы высшего образования во Франции, в частности в создании Нормальной и Политехнической школ. Основные работы в области небесной механики, в которой он достиг выдающихся результатов, подытоженных в пятитомнике "Трактат о небесной механике" (1798 - 1825). Сделал почти все то, чего не смогли сделать его предшественники для объяснения движения тел Солнечной системы на основе закона всемирного тяготения. Решил сложные проблемы движения планет и их спутников, Луны, разработал теорию возмущения небесных тел, предложил новый способ вычисления их орбит, доказал устойчивость Солнечной системы в течение очень длительного времени, открыл причину ускорения в движении Луны. Предложил (1796) гипотезу происхождения Солнечной системы. Физические исследования относятся к молекулярной физике, теплоте, акустике, электричеству, оптике. В 1821 установил закон изменения плотности воздуха с высотой (барометрическая формула). В 1806 - 1807 разработал теорию капиллярности, впервые используя представление, что молекулярное притяжение обнаруживается лишь на малых расстояниях, дал формулы для определения капиллярного давления (формула Лапласа). Вывел (1816) формулу для скорости звука в газах с поправкой на адиабатность. Вместе с А. Лавуазье впервые применял для измерения линейного расширения тел зрительную трубу, при помощи сконструированного ими ледяного калориметра определил (1783) удельную теплоемкости многих веществ. Активно выступал против гипотез флогистона. Придал общий вид закону Био-Савара в электродинамике. Как председатель Палаты мер и весов активно внедрял в жизнь новую математическую систему мер. В философии естествознания стоял на позициях стихийного материализма, его взгляды были близки к взглядам французских материалистов. В математике известен "оператором Лапласа, "интегратором Лапласа", "преобразованием Лапласа, "интегралом Лапласа", "уравнением Лапласа", "теоремой Лапласа", является одним из создателей теории вероятностей. Член Петербургской АН (1802).
Гаусс Карл Фридрих (Gauss C.)(30.IV.1777-23.II.1855) Родился в Брауншвейге. С раннего детства
обнаружил выдающиеся математические
способности. В 1795-1798 гг. учился в Геттингенском
университете. Математические вычисления
заменили Гауссу обычные детские игры. Он делил
единицу на все простые числа р и первой тысячи
подряд, подмечая, что десятичные знаки рано или
поздно начинают повторяться. Рассмотрев большое
количество примеров, Гаусс доказал, что число
цифр в периоде не превосходит Ученый доказал, что правильный n-угольник, где
n-число простое, может быть построен циркулем и
линейкой в том, и только в том случае, когда n
имеет вид С этого момента девятнадцатилетний Гаусс окончательно решил заниматься математикой (до этого он не мог сделать выбор между математикой и филологией). И всего через 9 дней в его дневнике появляется запись о втором открытии. Гаусс доказал так называемый квадратичный закон взаимности - один из основных в теории чисел. Этот закон открыл еще Л. Эйлер, но доказать его не смог. С именем Гаусса связаны многие замечательные страницы в истории математики. Он дал доказательство основной теоремы алгебры (всякое алгебраическое уравнение с комплексными коэффициентами имеет корень). Гаусс создал теорию поверхностей. До него были изучены геометрии только на двух поверхностях: на плоскости (планиметрия Евклида) и на сфере (сферическая геометрия). Гаусс нашел способ построения геометрии на любой поверхности роль прямых, как мерить расстояния между точками на поверхности и т. д. Теория Гаусса получила название внутренней геометрии. Он не опубликовал своих работ по неевклидовой геометрии и теории эллиптических функций. Эти результаты были открыты заново младшими современниками: русским математиком Н. И. Лобачевским и венгерским математиком Я. Бойли в первом случае и норвежским математиком Н. Абелем и немецким математиком К. Якоби - во втором. Гаусс занимался также астрономией, электромагнетизмом. Ему удалось вычислить орбиту малой планеты (астероида) Цереры. Решение этой сложной задачи принесло ученому известность, и он был приглашен заведовать кафедрой математики и астрономии, с которой была связана должность директора Геттингенской обсерватории. Этот пост Гаусс не покидал до конца жизни. Результаты своих исследований по астрономии Гаусс объединил в фундаментальном труде "Теория движения небесных тел".
Работы относятся к акустике, электромагнетизму, оптике, гидромеханике. Изобрел прибор для определения частоты звука (колесо Савара), изучал акустический резонанс, разрабатывал физические основы конструирования струнных инструментов, предложил конструкцию сирены. Показал (1826), что характер распространения звука в жидкостях такой же, как и в твердых телах. Проводи исследования пределов слышимости звука, в 1830 установил верхний предел слышимости - 24000 Гц, в 1831 нижний предел - 14-16 Гц. В 1820 вместе с Ж. Био экспериментально открыл закон электродинамики, определяющий величину напряженности магнитного поля, создаваемого электрическим током (закон Био-Савара). Изобрел для изучения поляризованного света кварцевую пластинку (пластинка Савара), полярископ (1840) [405, 557].
Исследования в области электричества, магнетизма, электрохимии. В 1821 впервые осуществил вращение магнита вокруг проводника с током и проводника с током вокруг магнита, создав тем самым лабораторную модель электродвигателя. В этом опыте наглядно проявилась связь между электрическими и магнитными явлениями. Не случайно, что в этом же году Фарадей поставил себе целью "превратить магнетизм в электричество". В 1831 открыл явление электромагнитной индукции - возникновение электрического тока в проводнике при изменении магнитного потока через контур проводника. В последующие годы подробно изучил открытое им явление и установил законы электромагнитной индукции, открыл (1835) экстратоки при замыкании и размыкании и установил их направление. Используя огромный экспериментальный материал, Фарадей доказал тождественность известных тогда видов электричества: "животного", "магнитного", термоэлектричества, электричества, возникающего от трения, гальванического электричества. Стремление выяснить природу электрического тока привело его к экспериментам по прохождению тока через растворы кислот, солей и щелочей. Результатом этих исследований было открытие в 1833 законов электролиза (законы Фарадея). Кроме большого практического значения, эти законы стали также существенным аргументом в пользу дискретного характера электричества. Ввел понятия: подвижность (1827), катод, анод, ионы, электролиз, электролиты, электроды (1834), изобрел (1833) вольтметр. В1845 открыл диамагнетизм и в 1847 - парамагнетизм. Обнаружил (1845) явление вращения плоскости поляризации света в магнитном поле (эффект Фарадея). Последнее было первым экспериментальным доказательством связи между светом и магнетизмом и положило начало магнитооптике. В работах Фарадея по электромагнетизму важным также является понятие поля. Он первый в 30-х годах ввел понятие поля, в 1845 употребил термин "магнитное поле", отчетливо сформулировал свою концепцию поля в 1852. По мнению А. Эйнштейна, идея поля была самой оригинальной идеей Фарадея, Самым важным открытием со времен Ньютона. У Ньютона и других ученых пространство выступало как пассивное вместилище тел и электрических зарядов, у Фарадея же пространство участвует в явлениях. "Надо иметь могучий дар научного предвидения, - писал Эйнштейн, чтобы распознать, что в описании электрических явлений не заряды и не частицы описывают суть явлений, а скорее пространство между зарядами и частицами". Для описания электрических и магнитных явлений Фарадей ввел представление об электрических и магнитных силовых линиях, которые он, правда, считал реально существующими. Является создателем учения об электромагнитном поле. В 1846 в мемуаре "Мысли о лучевых колебаниях" высказал идею об электромагнитной природе света. В 1837 обнаружил влияние диэлектриков на электрическое взаимодействие (поляризацию диэлектриков) и ввел понятие диэлектрической проницаемости. Высказал мысль о распространении электрического и магнитного взаимодействий через промежуточную среду. В1843 экспериментально доказал закон сохранения электрического заряда. Близко подошел к открытию закона сохранения и превращения энергии, высказав в 1840 мысль о единстве сил природы (различных видов энергии) и их взаимном превращении. Был популяризатором физики, в частности широко известна его книга "История свечи", переведенная почти на все языки мира. В 1830 году член Петербургской АН. Лобачевский Николай Иванович(1.XII.1792-24.II.1856) С 14 лет жизнь Н. И. Лобачевского была связана с Казанским университетом. Его студенческие годы приходились на благополучный период в истории университета. Было у кого учиться математике: среди профессоров выделялся М. Ф. Бартельс, сотоварищ первых шагов в математике К. Гаусса. С 1814 г. Лобачевский преподает в университете: читает лекции по математике, физике, астрономии, заведует обсерваторией, возглавляет библиотеку. В течение нескольких лет он избирался деканом физико-математического факультета. С 1827 г. начинается 19-летний период его непрерывного ректорства. Все надо было начинать заново: заниматься строительством, привлекать новых профессоров, менять студенческий режим. На это уходило почти все время. Еще в первых числах февраля 1826 г. он передал в университет рукопись "Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных", 11 февраля он выступил с докладом на заседании совета университета. Собственно, речь шла не о доказательстве пятого постулата Евклида, а о построении геометрии, в которой имеет место его отрицание, т. е. о доказательстве его невыводимости из остальных аксиом. Вероятно, никто из присутствовавших не мог уследить за ходом мысли Лобачевского. Созданная комиссия из членов совета несколько лет не давала заключения. В 1830 г. в "Казанском вестнике" выходит работа "О началах геометрии", представляющая собой извлечение из доклада на совете. Чтобы разобраться в ситуации, решили воспользоваться помощью столицы: в 1832 г. статью послали в Петербург. И здесь никто ничего не понял, работа была квалифицирована как бессмысленная. Ничто не могло поколебать уверенности Лобачевского в своей правоте. В течение 30 лет он продолжает развивать свою геометрию, пытается делать изложение более доступным, публикует работы на французском и немецком языках. Немецкую версию изложения прочитал Гаусс и, разумеется, понял автора с полуслова. Он прочитал его работы на русском языке и оценил их в письмах к ученикам, но публичной поддержки новой геометрии не оказал. Н. И. Лобачевский дослужился до высоких чинов, он был награжден большим числом орденов, пользовался уважением окружающих, но о его геометрии предпочитали не говорить, даже в те дни, когда Казань прощалась с ним. Прошло еще не менее двадцати лет, прежде чем геометрия Лобачевского завоевала права гражданства в математике. Остроградский Михаил Васильевич(24.IX.1801-1.I.1862) М. В. Остроградский- русский математик, один из основателей петербургской математической школы, академик Петербургской академии наук (1830). Основополагающие работы И. Ньютона и Г. Лейбница дали математический аппарат для исследования тех проблем механики и астрономии, которые сводились к функциям одного аргумента (времени). Но целый ряд вопросов физики приводил к рассмотрению функций, зависящих от многих переменных. Необходимость решать задачи, касающиеся функций многих переменных, привела к созданию новой области математики, получившей название теории уравнений математической физики. Развивая методы решения таких уравнений, предложенные в частном случае еще в XVIII в., Ж. Фурье свел их решение к разложению функций по тригонометрическим функциям. Остроградский рассмотрел подобные задачи для тел, имевших более сложную форму, чем изученные Фурье. Еще в своей первой работе, посвященной распространению волн в сосуде цилиндрической формы, он решил задачу, на которую объявила конкурс Парижская академия наук. А в 1828 г. ученый дал общую формулировку метода Фурье и изучил с его помощью колебания газа, упругих пластинок и т. д. М. В. Остроградскому удалось обобщить формулу интегрального исчисления, выведенную в одном частном случае К. Гауссом. Физический смысл формулы Гаусса-Остроградского состоит в том, что поток жидкости через замкнутую поверхность равен суммарной производительности находящихся внутри нее источников и стоков. Плодотворно занимался Остроградский теоретической механикой, математическим анализом и т. д. Многие его работы имели прикладную направленность: ученый занимался внешней баллистикой, статистическими методами браковки изделий, участвовал в комиссиях по реформе календаря, по водоснабжению Петербурга. Он был основателем научной школы русских ученых, работавших в области механики и прикладной математики и воспринявших от своего учителя принцип сознательного сочетания теории с практикой. Много внимания Остроградский уделял проблемам преподавания математики. Он считал, что главная задача обучения - заинтересовать ребенка, а элементы наук должны излагаться в наиболее доступной и приспособленной к уму ученика форме. Абстрактное же изложение математики отвращает учеников от изучаемой науки. Эти идеи Остроградского легли в основу движения за реформу математического образования в России, начавшегося во второй половине XIX в.
Максвелл много сделал для развития математической физики. Его научные труды касаются проблем электромагнетизма, молекулярной физики, оптики, механики, теории упругости и другое. Важнейшим достижением Максвелла была созданная им электромагнитная теория света, хотя и другие его работы - по основам графической статики, о структуре, устойчивости и движении колец Сатурна, кинетическая теория газов - также представляют большой интерес. Когда Максвелл анализировал электромагнитные явления, их законы считались хорошо известными, однако математически они не были полностью сформулированы. Максвелл первый сделал попытку создать общую теорию электромагнетизма. Его исследования послужили толчком для создания теории электрона Лоренца, открытия электромагнитных волн и теории относительности Эйнштейна. В работах Максвелла нашли применение и получили дальнейшее развитие идеи Гамильтона о целесообразности приложения векторного анализа и символических дифференциальных операторов. Он способствовал формированию векторного исчисления в виде отдельной математической дисциплины. Пуанкаре Анри (Poincare H. J.)(29.IV.1854 - 17.VII.1912) Французский математик, физик, астроном и философ, член Парижской Академии Наук (1887), и более чем 35 иностранных академий, в том числе иностранный почетный член Петербургской Академии Наук. Родился в Нанси (Лотарингия). Начальное образование получил дома. Окончил с отличием колледж в Нанси (1870). С 1873 учился в Политехнической школе, а в 1875 - 1879 - в Горной. Защитил в Парижском университете Диссертацию на степень доктора математических наук, в 1879 - 1881 преподавал математический анализ в Каннском, а в 1881 -1885 - в Парижском университетах. С 1886 - профессор математической физики и теории вероятностей, а с 1895 - и небесной механики в Парижском университете. Нет области математики или ее применений, где бы Пуанкаре не оставил новых методов исследования. Его работы, опубликованные Парижской Академией Наук в 1916 - 1954, составляют 10 томов. Пуанкаре принадлежат разнообразные исследования в области топологии, теории дифференциальных уравнений, теории вероятностей, теории автоморфных функций, неевклидовой геометрии и других разделов математической науки. Пуанкаре занимался математической физикой, в частности теорией потенциала, теорией теплопроводности, а также решением разных задач механики и астрономии. В 1904 - 1905 высказал принцип относительности в качестве всеобщего и строгого положения, показал, что невозможно обнаружить абсолютное движение, исходя из представлений об эфире и уравнений Максвелла - Лоренца. Ввел термины "преобразование Лоренца", "группа Лоренца". Независимо от А. Эйнштейна заложил основы специальной теории относительности. Построил первый вариант релятивистской теории гравитации. Как философ Пуанкаре известен своими трудами по общеметодологическим проблемам науки, тяготел к махистам. В интерпретации науки и ее законов является основателем конвенционализма. В.И. Ленин в работе "Материализм и эмпириокритицизм" подверг критике его философских взглядов. Приложение II
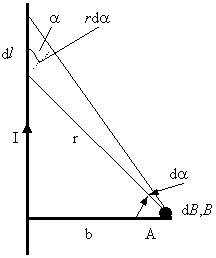
Мы имеем два закона и две полевые теоремы и хотим показать расчет цилиндрических полей с их помощью. Применяем закон Био-Савара-Лапласа для магнитного поля прямого тока. В произвольной точке А векторы dB от всех элементов тока имеют одинаковое направление - за плоскость рисунка. Поэтому сложение векторов dB можно заменить сложением их модулей dB, причем
Из рисунка видно, что
Интегрируя это выражение от
Закон Био-Савара-Лапласа. При помощи теоремы о циркуляции вектора магнитной индукции определим этот вектор. Найдем магнитное поле внутри бесконечно длинного провода круглого сечения. Ток I в проводе постоянный. За контур выберем
поверхность. Везде на контуре угол между Вi и
Это теорема о циркуляции. Применим закон Кулона и теорему Гаусса для
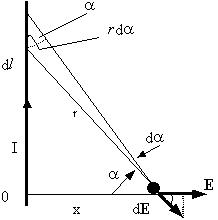
электрического поля Е равномерно заряженнной
нити. Из соображения симметрии ясно, что вектор Е
должен иметь направление, показанное на рисунке.
Найдем составляющую
Где
Теперь возьмем интеграл по
Закон Кулона. Поле равномерно заряженной прямой нити. Применим теорему Гаусса к расчету электрического поля Е.
Если заряд находится в центре проводящей нити, то везде на нити, в силу равноудаленности ее поверхности от заряда модуль напряженности поля, будет постоянным, а угол между вектором напряженности и вектором нормали к поверхности равен 0, так как направлены по радиусу поперечного сечения нити. Везде на поверхности:
Тогда получаем:
Преобразуем: сумма есть просто поверхность нити радиуса сечения R.
Получим:
Уравнения Максвелла. Для стационарных, неизменных во времени электрического поля Е и магнитного поля В, применив дважды (к каждому полю) теорему Гаусса и терему о циркуляции, мы получили систему уравнений, называемую уравнениями Максвелла: 1) поток вектора напряженности электрического поля Е сквозь замкнутую поверхность прямопропорционален алгебраической сумме зарядов, охватываемой этой поверхностью:
2) циркуляция вектора Е по любому замкнутому контуру равна нулю:
3) поток вектора индукции магнитного поля В сквозь произвольную замкнутую поверхность равен нулю:
4) циркуляция вектора В по любому замкнутому контуру прямопропорциональна алгебраической сумме токов, охватываемых этим контуром:
Литература:
Библиография
|
Близкий к описанному метод решения
задач был известен еще во II тысячелетии до н. э.
писцам Древнего Египта (однако они не применяли
буквенной символики). В сохранившихся до наших
дней математических папирусах имеются задачи,
которые приводят к уравнениям не только первой
степени с одним неизвестным, как в задаче о
возрасте братьев, но и вида 
построил в
1843 г. ирландский математик У. Гамильтон, который
назвал их кватернионами. Правила действия над
кватернионами напоминают правила обычной
алгебры, однако их умножение не обладает
свойством коммутативности: например,
,
применяя обращение рядов, т. е. Представляя x
через y, наше разложение в ряды показательной
функции, синуса, косинуса и т. д. 
а затем
рядом с ней: 
. Знак интеграла в современной форме
впервые встречается в его работе "О скрытой
геометрии…" (1686). Лейбниц решил проблему
касательных с помощью дифференциального
исчисления. При этом он изложил правила
дифференциального произведения, степени,
неявной функции. Эти результаты он опубликовал
только в 1684 году в статье "Новый метод
максимумов и минимумов", где впервые назвал
свой алгоритм дифференциальным исчислением. В 1693
Лейбниц опубликовал первые образцы
интегрирования дифференциальных уравнений с
помощью бесконечных рядов. 
, и это
постепенно привело его к первому открытию. 
Например,
если 
то
правильные трех-, пяти-, семнадцати - и
257-угольники можно построить циркулем и линейкой,
а семиугольник - нельзя. Еще древние математики (в
их числе Архимед) умели строить циркулем и
линейкой правильные n-угольники при 
и вообще
при 
, и
только такие. Ученые безуспешно пытались
построить правильный семиугольник, девяти
угольник. А Гаусс дал полное решение проблемы,
над которой трудились ученые в течение 2 тыс. лет.
и 
поэтому 
до 
, получаем
равен нулю.
Циркуляция вектора индукции магнитного поля
прямопропорциональна алгебраической сумме
пронизывающих контур токов, коэффициентом
пропорциональности служит магнитная постоянная.
от элемента 
нити с зарядом 
-
линейная плотность заряда. Приведем это
уравнение к виду, удобному для интегрирования. Из
рисунка видно, что 
и 
от 
до 
, получим 
| | На первую страницу | Поиск | Купить Matlab | |
|
|