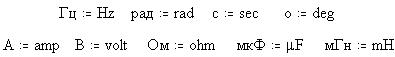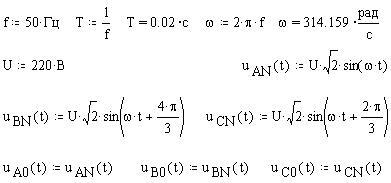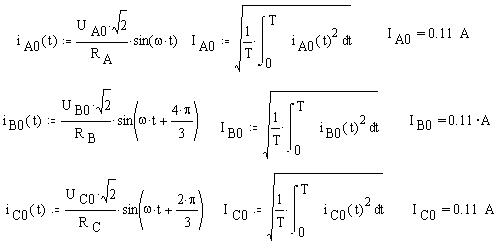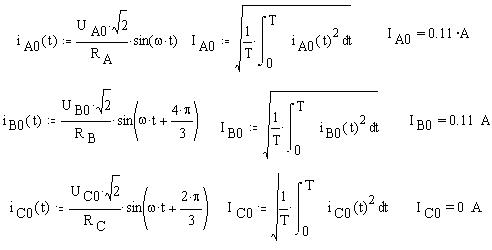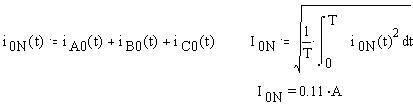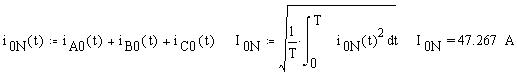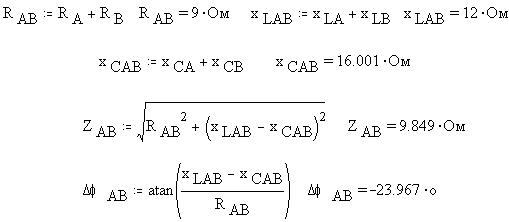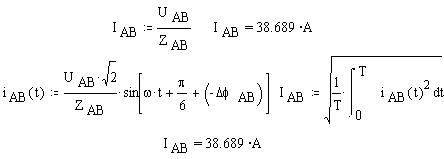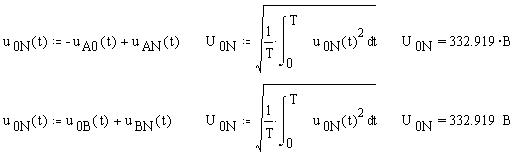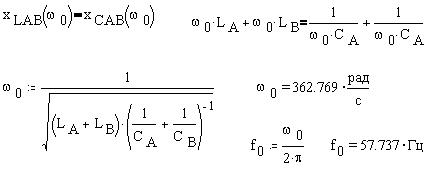| Купить Matlab | Mathematica | Mathcad | Maple | Statistica | Другие пакеты | |
| Internet-класс | Примеры | Методики | Форум | Download | |

|
|
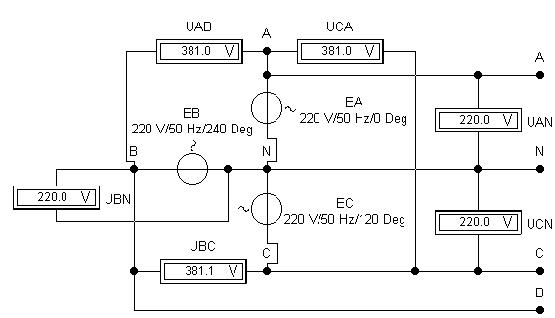
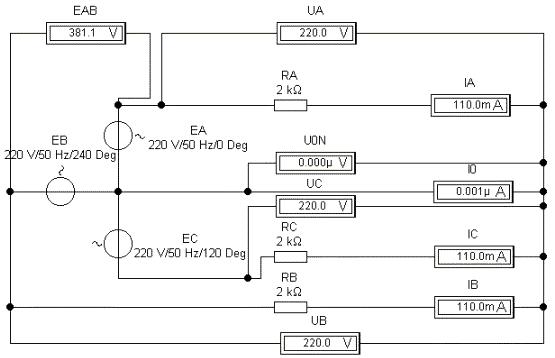
1. Источник трёхфазного напряжения. Создадим в Electronics Workbench 5.12 электронную модель источника трехфазного напряжения синусоидального тока, использовав "виртуальные" модели источников напряжений однофазного синусоидального тока:
Начальные фазы напряжений "генераторных обмоток" фаз AN, BN и CN сдвинуты относительно друг друга на угол -120о (или + 240о, как на схеме), начала обмоток объединены в "нейтральную точку" N по схеме "звезда". Концы обмоток - линейные провода A, B и C. Вольтметры включены в моде AC (Alternating Current - переменный ток). Представим математическую модель "трехфазного генератора" в MathCAD. Введём единицы измерений:
Определим частоту f, период Т, угловую частоту w, действующие и мгновенные значения фазных напряжений:
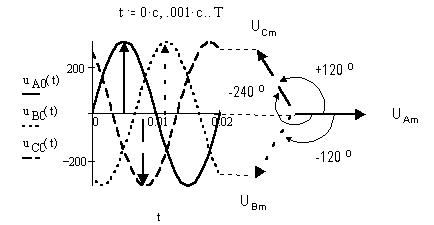
Построим графики - временные диаграммы фазных напряжений и в VISIO Exspress Drawing 3.0 векторную диаграмму:
2. Симметрично-активные нагрузки по схеме "звезда".
Найдём по закону Ома действующие значение силы тока в проводах, затем определим мгновенные значение токов и найдём действующие значения токов как средние квадратичные мгновенных значений за период:
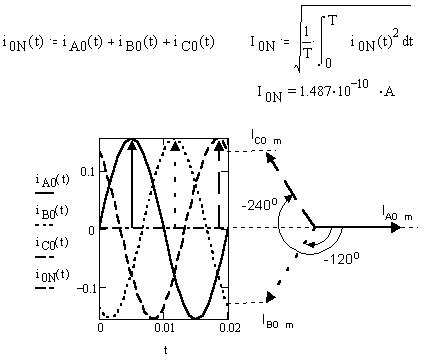
Определим мгновенное значение силы тока в нулевом проводе и его действующее значение:
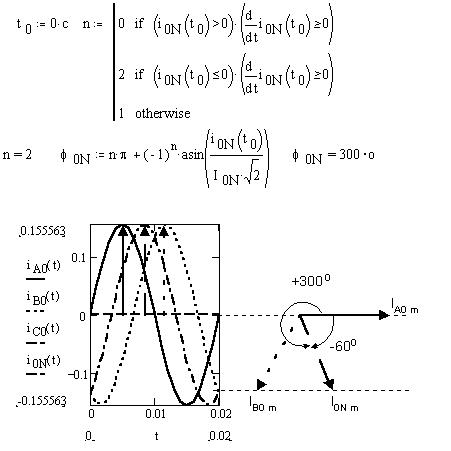
3. Аварийный режим работы: обрыв линейного провода С (RC = Ґ). Найдём по закону Ома действующие значение силы тока в проводах, затем определим мгновенные значение токов и найдём действующее значение токов как средние квадратичные мгновенных значений за период:
Определим мгновенное значение силы тока в нулевом проводе и его действующее значение:
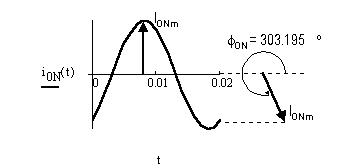
Найдём начальную фазу синусоиды i0N(t) и построим векторную диаграмму:
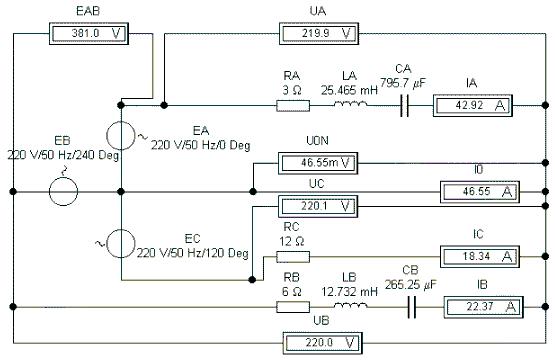
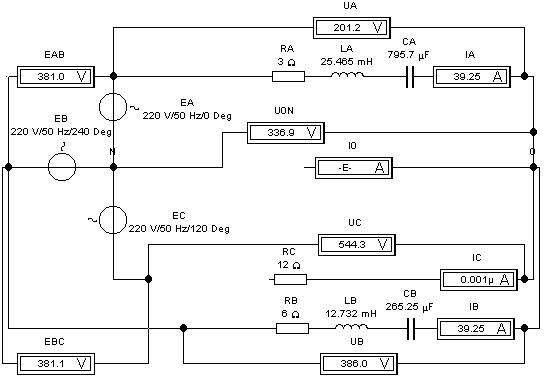
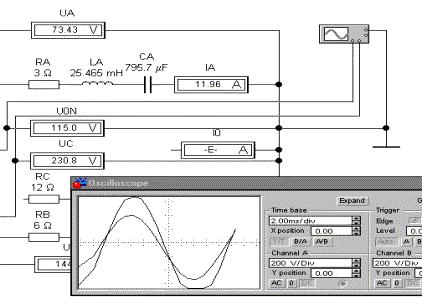
4. Несимметричная активно-реактивная нагрузка. Электронная модель предлагаемой ниже цепи реализована в электронной лаборатории Electronics Workbench 5.12, математическая модель - в MathCAD 6.0 PLUS.
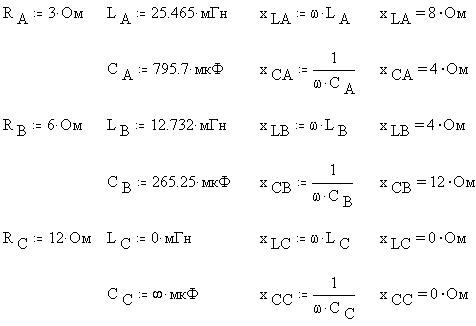
Введем значения активных, индуктивных и емкостных сопротивлений, соответствующих резисторам, индуктивностям и емкостям на электронной модели, в фазах A, B и C:
Найдем полные сопротивления и углы сдвига фаз между током и напряжением для каждой фазы:
Найдем по закону Ома действующие значение силы тока в фазах, затем определим мгновенные значение токов (с учетом сдвига фазы между напряжением и током) и найдем действующее значение токов как средние квадратичные мгновенных значений за период:
Определим мгновенное значение силы тока в нулевом проводе и его действующее значение:
Построим векторную диаграмму для тока i0N(t):
Обрыв линейного провода С и нулевого провода Рассмотрим электронную модель в Electronics Workbench 5.12 и определим показания приборов на математической модели в MathCAD 6.0 PLUS, показав их также на частотных характеристиках (резонансных кривых) участков цепи. Вычислим установившиеся значения для образовавшейся фазы AB, составленной из последовательно соединенных фазных нагрузок A0 и 0B и включенной под линейное напряжение UAB:
Активное, реактивные и полное сопротивления фазы AB равны:
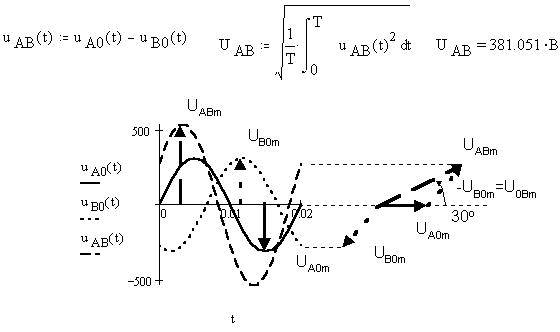
По закону Ома найдем действующее значение IAB величины силы тока в фазе AB. Определим
также функцию мгновенного значения iAB(t),
учтя, что, как это видно из диаграммы, линейное
напряжение UAB опережает фазное
напряжение UA на 30° и, кроме того,
учтем сдвиг фаз межу напряжением и током в фазе AB
Найдем по закону Ома показания вольтметров UA0 и U0B на участках A0 и 0B ветви AB с током IAB. Найдем эти же действующие значения как средние квадратичные мгновенных значений, в формулах которых учтем дополнительно сдвиг фаз между током IABи напряжениями на участках:
Вычислим напряжение смещения между нулем и нейтралью в аварийной цепи сначала против направления тока в фазе 0A и по генераторной обмотке AN, затем вдоль тока в фазе 0B и по генераторной обмотке BN:
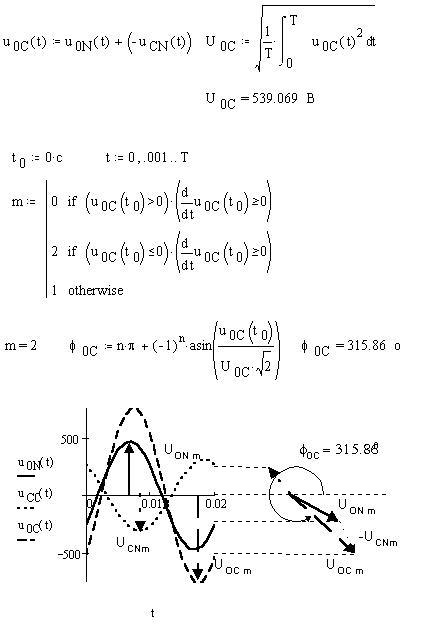
Аналогично определим мгновенное значение напряжения между нулем и узлом C, учтя, что генераторную обмотку проходим в направлении NC, найдем действующее его значение - показание соответствующего вольтметра на электронной модели. Найдем также начальную фазу синусоиды u0C(t) и построим векторную диаграмму:
Рассмотрим также осциллограммы напряжений u0N(t) и u0C(t) в электронной модели:
Определим индуктивные и емкостные сопротивления участков A0 и 0B как функции угловой частоты. Определим также суммарное активное и реактивные сопротивления фазы AB, полные сопротивления участков A0 и 0B, а также всей фазы AB как функции угловой частоты:
Для определения диапазона изменения угловой частоты и построения графиков частотных характеристик найдем резонансную частоту фазы AB из условия, что на этой частоте выполняется равенство величин индуктивного и емкостного сопротивлений, откуда следует формула Томсона для резонансной частоты w0:
Как видим, при обрыве линейного провода фаза AB оказалась почти в резонансе напряжений. Определим также величину угловой частоты w1, соответствующей рабочей частоте 50 Гц, и укажем диапазон изменения угловой частоты:
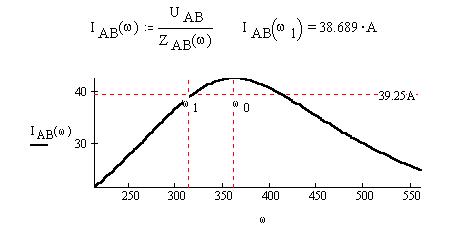
Построим частотную характеристику силы тока в фазе AB, найденной по закону Ома, и отметим на ней рисками угловые частоты w0, w1 (по оси X) и показание амперметра из электронной модели (по оси Y):
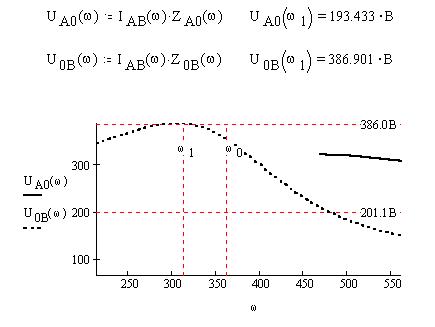
Определим по закону Ома частотные характеристики напряжений на участках A0 и 0B фазы AB и отметим на графиках этих характеристик показания вольтметров из электронной модели:
Содержание |
| | На первую страницу | Поиск | Купить Matlab | |
|
|