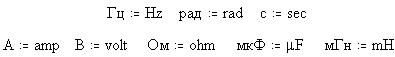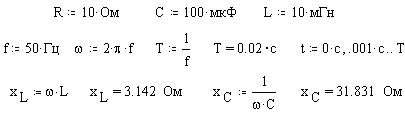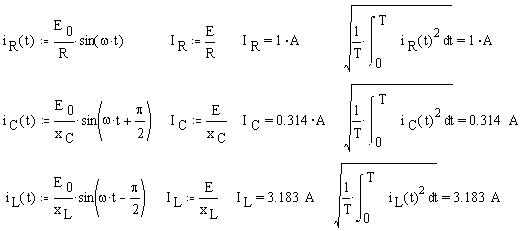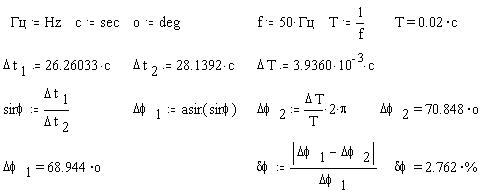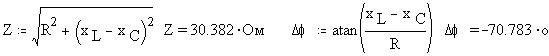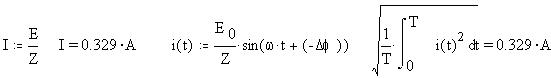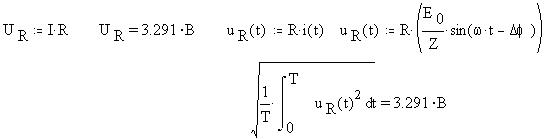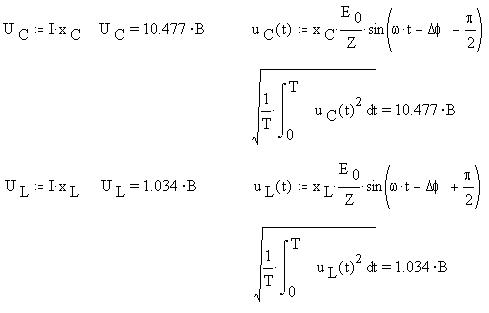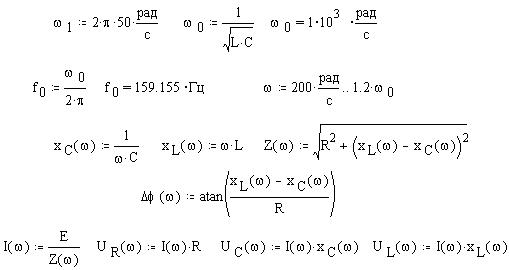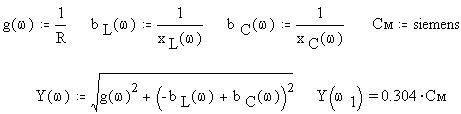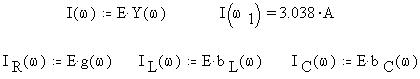| Купить Matlab | Mathematica | Mathcad | Maple | Statistica | Другие пакеты | |
| Internet-класс | Примеры | Методики | Форум | Download | |

|
|
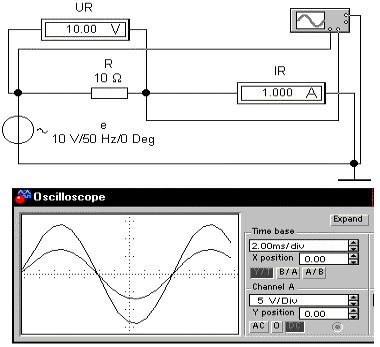
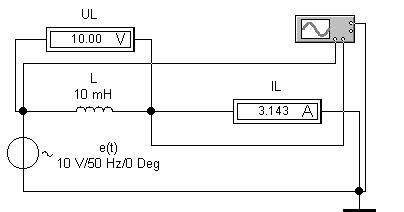
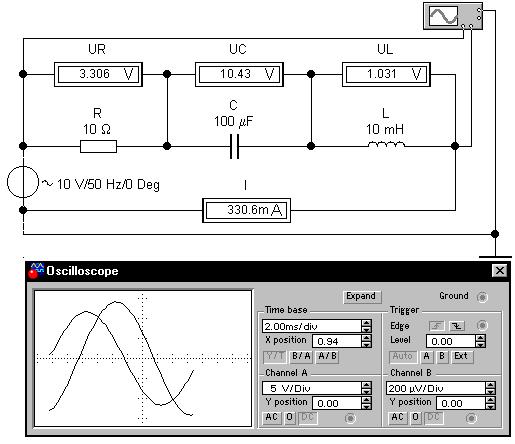
Создадим в Electronics Workbench 5.12 электронную модель резистора в цепи синусоидального тока:
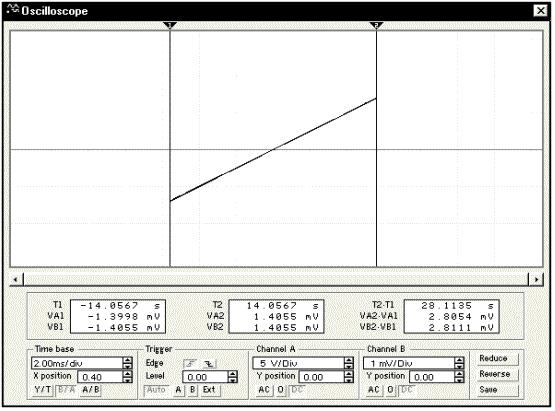
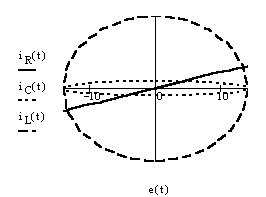
Источник синусоидального напряжения e(t): действующее значение равно 10 В, частота 50 Гц, начальная фаза 0о. Амперметр и вольтметр включены в моде AC (Alternating Current - переменный ток). Напряжение источника с исследуемого резистора R подаем на канал A осциллографа (Oscilloscope). Напряжение, прямо пропорциональное силе тока в цепи, подаем с амперметра, внутреннее сопротивление которого по умолчанию равно 1 мОм, на канал B по схеме характериографа. Такое малое активное сопротивление практически не повлияет на сдвиг фаз между током и напряжением в активно-реактивных цепях синусоидального тока. В режиме Y/T получаем временные диаграммы напряжения и тока. В режиме B/A - фазовую диаграмму (график причинно-следственной связи между напряжением на резисторе и силой тока - закон Ома). Фазовая траектория линейна, ток и напряжение совпадают по фазе (как это хорошо видно и по временным диаграммам на рисунке выше):
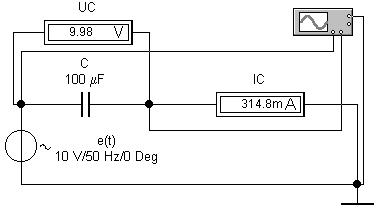
Перетаскивая мышью стрелки 1 и 2, перемещаем вертикальные курсоры. В окнах отображаются моменты времени и уровни сигналов каналов A и B в месте пересечения курсоров с диаграммами, а также разность этих величин. Ознакомимся с основными установками прибора. Период развертки (Time base) можно установить от 0.10 нс/дел до 1с/дел. Позиция начала показа сигнала по горизонтали (X position): от -5.00 до 5.00 (сдвиг сигнала, в делениях, влево, вправо), - если 0, то начало вывода сигнала - левый край экрана. Кнопки Y/T, B/A и A/B: вывод сигналов входных каналов, соответственно, во времени и относительно друг друга. Смещение по вертикали (Y position) выводимых сигналов (от -3.00 до 3.00) - в делениях по отношению к оси X. Усиление каналов по вертикали (V/div - Volts per Division): от 0.01 мВ/дел до 5 кВ/дел. Тип входного соединения (Input Coupling) AC, 0, DC: соответственно, канал не пропускает постоянную составляющую сигнала (эквивалентно подключению последовательно ко входу конденсатора), выводит горизонтальную линию на установленном смещении сигнала по вертикали или выводит сумму постоянной и переменной составляющих сигнала. Установки вывода сигнала на экран (Trigger): вывод с положительного или отрицательного полупериода (Trigger Edge); уровень сигнала, с которого начинается вывод на экран (Trigger Level): от -3.00 до 3.00 дел.; вывод относительно внешнего сигнала (Trigger Signal - External). Заземление осциллографа (Groundig): не обязательно, если подключенная цепь уже заземлена. Создадим теперь модель емкости в цепи синусоидального тока:
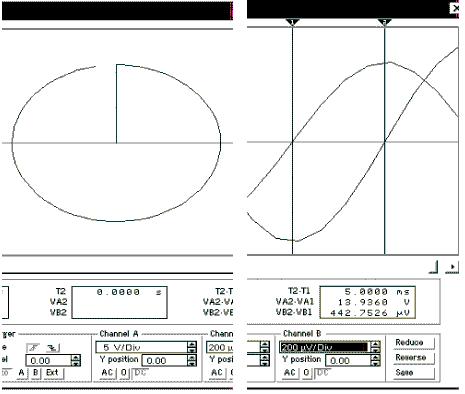
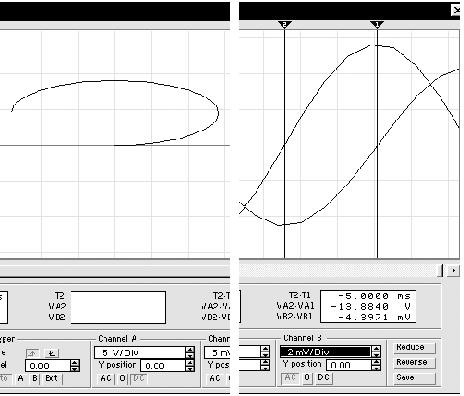
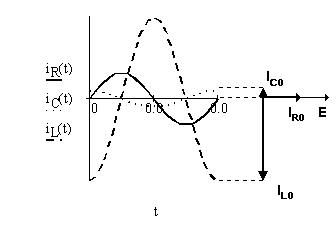
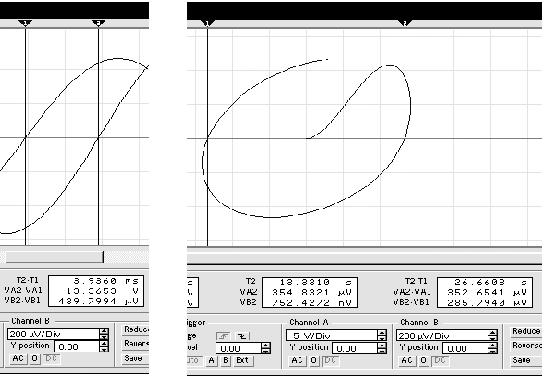
Рассмотрим фазовую и временные диаграммы:
Первая представляет собой симметричный относительно вертикальной оси эллипс с "закруткой" по часовой стрелке (направление движения точки фазового состояния хорошо заметно после включения цепи): ток опережает напряжение на 90°, и на временных диаграммах при частоте источника напряжения, равной 50 Гц, синусоида тока (курсор 1) опережает синусоиду напряжения (курсор 2) на 5 мс или на четверть периода, равного 20 мс при указанной частоте. Аналогично представим модель индуктивности:
Рассмотрим фазовую и временные диаграммы:
Здесь фазовая кривая представляет собой симметричный относительно вертикальной оси эллипс с "закруткой" против часовой стрелки: ток отстает от напряжения на 90°, и на временных диаграммах синусоида тока (курсор 1) отстает от синусоиды напряжения (курсор 2) на 5 мс. Представим теперь в MathCAD 6.0 PLUS математические модели для показанных выше электронных моделей элементов цепей синусоидального тока. Определим через встроенные переменные размерностей "русские" размерности:
Введем значения параметров элементов цепей и частоты; найдем величину периода и определим дискретный арумент t с шагом 0.001 с для построения декартовых графиков; найдем значения реактивных сопротивлений:
Определим параметры источника напряжения и временную функцию мгновенных значений напряжения:
Определим по закону Ома функции мгновенных значений токов через моделируемые элементы цепей; найдем действующие значения токов и по закону Ома, и как средние квадратичные мгновенных значений:
Создадим декартов график мгновенных значений токов и построим как объект приложения Visio Express for MathCAD векторные диаграммы токов (для удобства построения в технологии drag and drop, за модули векторов примем не действующие, а амплитудные значения мгновенных величин):
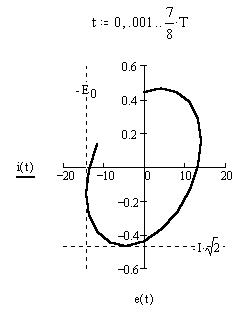
Представим параметрически соответствующие фазовые диаграммы:
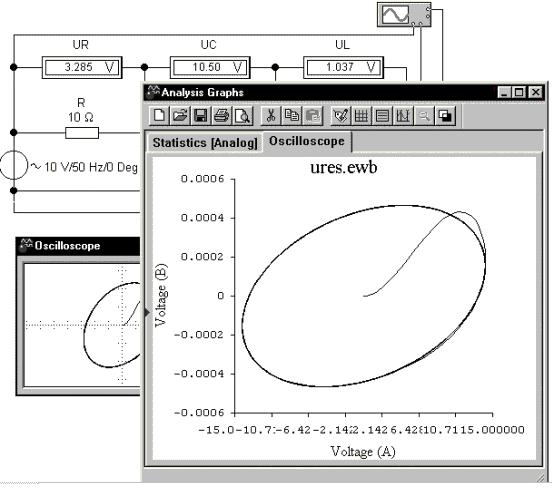
Объединим рассмотренные элементы последовательно:
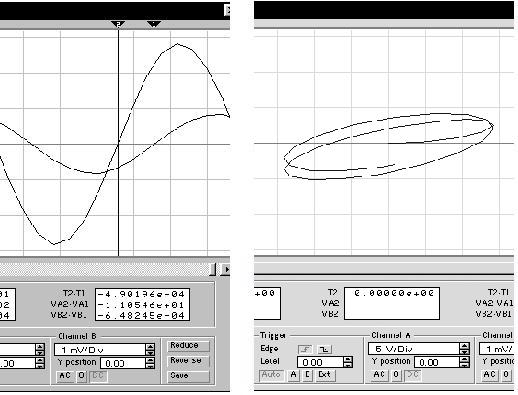
Рассмотрим временные и фазовую диаграммы цепи в окне осциллографа, а также в окне аналитических графиков. Как видим, цепь носит активно-емкостный характер: ток опережает напряжение на менее четверти периода - на 3.9360 мс; фазовая кривая "закручивается" по часовой стрелке:
Угол сдвига фаз между током и напряжением определяется как по временным, так и по фазовой диаграммам. В последнем случае синус угла равен отношению промежутка между точками пересечения фазовой кривой любой координатной оси к максимальному размеру эллипса по этой оси. Найдем первую величину (по горизонтальной оси): в окне осциллографа, а вторую, добавив курсоры, в окне аналитических графиков, - это, соответственно, Т2 - Т1 = 26.6603 с и dx = 28.1392 с. По временным осциллограммам определим интервал сдвига: Т2 - Т1 = 3.9360 мс. Рассчитаем угол сдвига фаз и относительную погрешность двух методов в MathCAD:
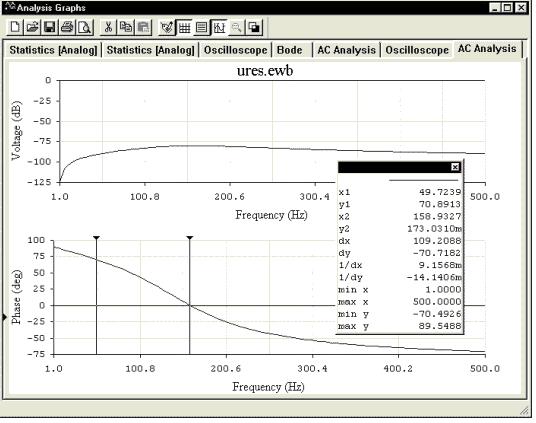
В Electronics Workbench 5.12 легко получить аналогичный результат, воспользовавшись все тем же окном аналитических графиков, включив в него командой "AC Frequency…" из меню "Analysis" закладку частотной зависимости напряжения и фазы тока относительно напряжения в цепи, подключенной к любому источнику синусоидального напряжения. Найдем на нижнем графике зависимости угла сдвига фаз от частоты, добавив курсоры, сдвиг фаз на частоте 50 Гц (y1) и на резонансной частоте (y2: Phase = 0), которую определим по этому же графику (x2):
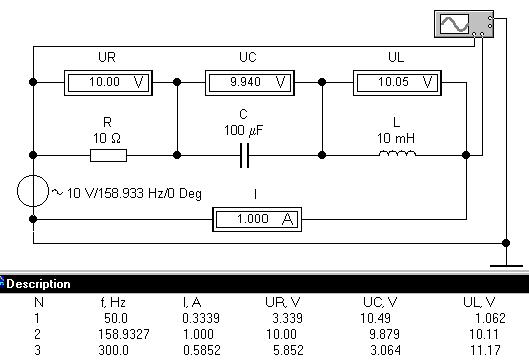
Проведем эксперимент в "ручном" режиме с записью данных в окне "Description" на частотах: 50 Гц, резонансной 158.9327 Гц, где характер цепи чисто активный, и 300 Гц, где характер цепи активно-индуктивный:
Рассмотрим в подтверждение сказанного временные и фазовую диаграммы на частоте 300 Гц:
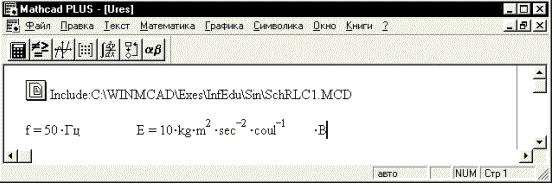
Рассчитаем показания приборов в электронной модели для частоты 50 Гц в MathCAD 6.0 PLUS. Внедрим в новый документ рассмотренный выше документ с определениями размерностей, частоты, периода и параметров источника напряжения. Ниже пиктограммы с адресом внедренного документа все его определения, как видим, выполняются:
Определим полное сопротивление (импеданс) цепи и угол сдвига фаз между током и напряжением:
Найдем по закону Ома действующее значение тока. Определив функцию мгновенных значений силы тока с учетом сдвига фаз между напряжением и током, найдем действующее значение силы тока и как среднее квадратичное мгновенных значений:
Найдем по закону Ома действующее значение напряжения на активном сопротивлении R. Определив функцию мгновенных значений, найдем её среднее квадратичное:
Аналогично, с учетом дополнительного сдвига по фазе на четверть периода между током и напряжением на реактивных элементах, найдем действующие значения напряжений на емкости C и индуктивности L:
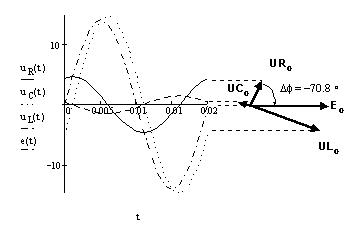
Построим графики мгновенных значений напряжений и в Visio Express for MathCAD создадим векторную диаграмму напряжений:
По-прежнему, для удобства построения в технологии drag and drop, за модули векторов приняты не действующие, а амплитудные значения мгновенных величин. Построим также фазовую диаграмму цепи, обозначив на ней рисками амплитудные значения напряжения и силы тока:
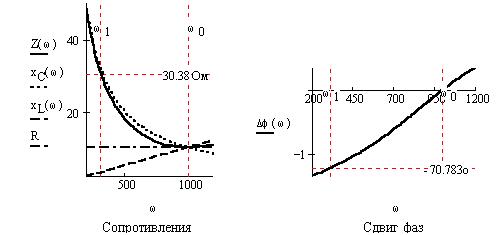
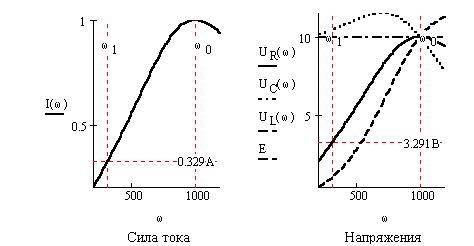
Определим частотные зависимости реактивных и полного сопротивлений, силы тока в цепи, напряжений на элементах:
Построим графики соответствующих величин:
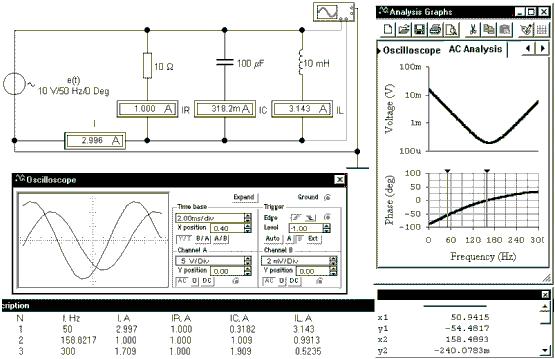
От резонанса напряжений перейдем к резонансу токов, для чего соединим те же компоненты цепи R, C и L параллельно. Проведем измерение токов ветвей и полного тока на частотах 50 Гц, 158.4893 Гц и 300 Гц. Результаты запишем в окно "Description". Временные диаграммы напряжения источника (канал A осциллографа) и напряжения, прямо пропорционального полному току и снимаемого с "общего" амперметра (канал B), показывают активно-индуктивный характер цепи на частоте 50 Гц: осциллограмма тока отстает во времени от графика напряжения. Диаграммы частотного анализа в окне аналитических графиков показывают, во-первых, увеличение полного сопротивления цепи на резонансной частоте и, во-вторых, переход фазы тока относительно напряжения с отрицательного значения (активно-индуктивная цепь) на положительное (активно-емкостная). В резонансе цепь ведет себя как чисто активная, общий ток равен току через резистор, - энергетические процессы в реактивных элементах полностью "возмещают" друг друга:
Определим в MathCAD частотные зависимости проводимостей (ветвей и полной), а также единицу их измерения; найдем проводимость цепи на частоте 50 Гц:
Определим затем частотные зависимости полного тока в цепи и токов её ветвей:
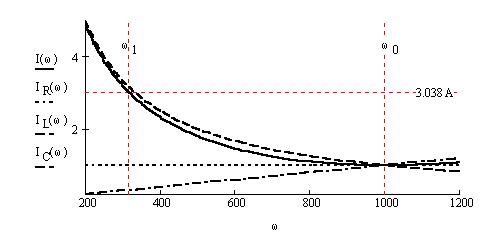
Построим теперь графики частотных характеристик. Графики проводимостей, токов и мощностей - геометрически подобны (физические величины отличаются в E и E2 раз), поэтому ограничимся резонансными кривыми токов:
Литература:
Содержание |
| | На первую страницу | Поиск | Купить Matlab | |
|
|