Вернуться
на страницу <Методические разработки>
Содержание
MathCAD 6.0: практическое пособие для
старшеклассников
Настоящее пособие отражает опыт работы
сотрудников МГДТДиЮ, МИРЭА, школ и межшкольных
учебных комбинатов по внедрению средств НИТ в
непрерывный образовательный процесс. Оно
ориентировано как на систему дополнительного
образования (учебно-творческие коллективы в
сфере НИТ, радиотехники, электроники и
электротехники), так и на систему общего
образования (компьютерная поддержка курсов и
практикума по физике, математике, информационным
технологиям). Материалы могут быть использованы
для дистанционного образования, в т. ч.
учащихся-инвалидов.
Учебный процесс на автоматизированном рабочем
месте (АРМ) учащихся, включающем ПЭВМ и
позволяющем использовать MathCAD 6.0, ставит
качественно новую задачу использования
элементов классической математики при изучении
соответствующих разделов физики и
профориентационных общетехнических дисциплин.
Цель предлагаемого учебного пособия -
эффективное практическое усвоение учащимися
старших классов основных возможностей базовой
версии MathCAD 6.0, а также знакомство с
профессиональной версией.
Электронная версия пособия готовится к
размещению на WWW-серверах МГДТДиЮ и МИРЭА в
разделе "Программно-методические фонды в
сфере НИТ".
- На досуге... - справочные
материалы
- От базовой версии- к
профессиональной
- HELP! - работа со справочной
системой MathCAD
Часть 2. Справочные материалы и работа со
справочной системой MathCAD 6.0
1. На досуге... - справочные материалы
Панель инструментов MathCAD 6.0 Basic
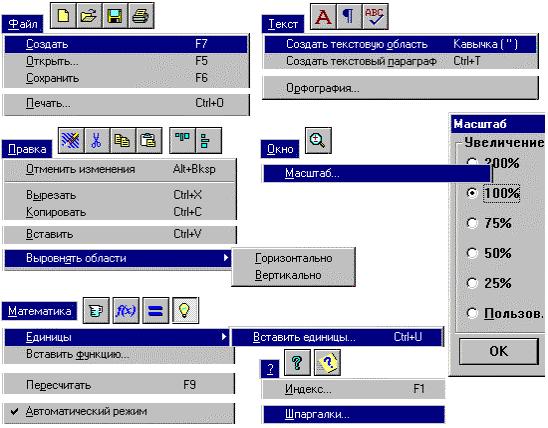
Встроенные функции MathCAD 6.0
Из числа основного набора функций,
поставляемого с MathCAD 6.0, мы рассмотрим лишь
наиболее часто применяемые в школе. Вставка функции
обеспечивается выбором команды Вставить
функцию... из меню Математика либо
кнопкой панели
инструментов. Вид диалогового окна: панели
инструментов. Вид диалогового окна:
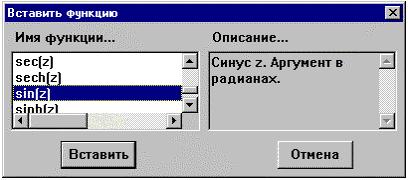
Разумеется, имя функции можно просто
напечатать с учетом формата MathCAD (заметим, что
имена встроенных функций не чувствительны к
шрифту, но чувствительны к регистру ).
Рассмотрим функции синус, арксинус и косинус
угла t, измеряемого по умолчанию в радианах:
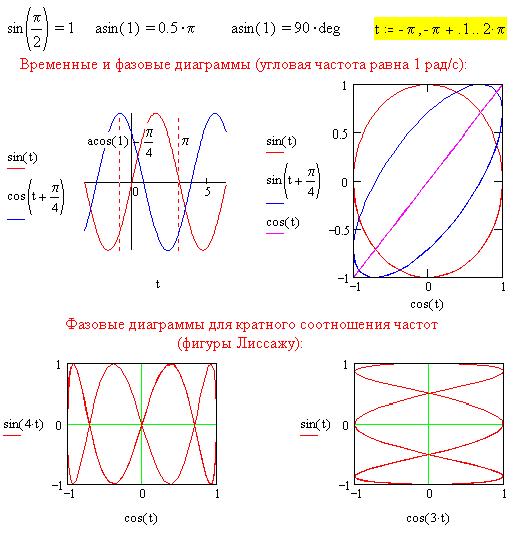
Рассмотрим теперь функции тангенс, арктангенс
и котангенс угла х:
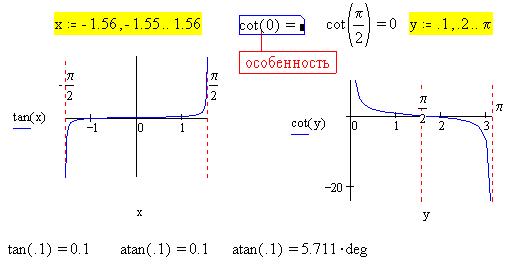
Отметим сообщение об ошибке
"Особенность" (при попытке вычислить
функцию или выполнить операцию с недопустимым
значением, - в данном случае - попытка деления на
0).
Рассмотрим теперь функцию "десятичный
логарифм числа":
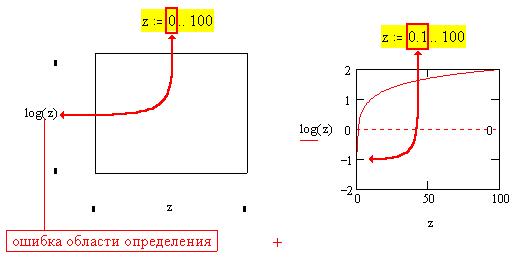
Смысл сообщения об ошибке и последующего
редактирования области определения дискретного
аргумента z понятен из рисунка.
Рассмотрим функцию floor(x) и ceil(x), возвращающих,
соответственно, наибольшее целое число 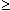 x и наименьшее целое число x и наименьшее целое число 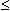 x: x:

Функция "мантисса(х)", введенная нами,
использует встроенную функцию.
Рассмотрим две логические функции MathCAD.
Первая функция if(условие, значение 1,
значение 2) возвращает значение 1, если
условие выполняется, иначе - возвращает
значение 2. Для определения условия используются
обычные логические операторы, вводимые кнопками
панели символов либо с клавиатуры как в таблице:

Рассмотрим два примера: функцию округления и
изменение по условию знака функции, используя
функции floor(x) и ceil(x), определенные выше.
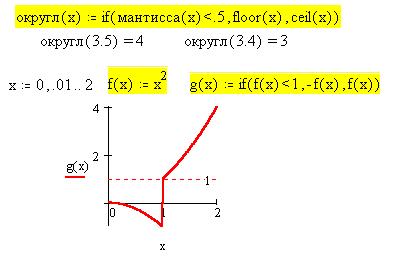
Вторая логическая функция until(x, z)
возвращает значение z, пока
выражение x (содержащее дискретный
аргумент) неотрицательно :
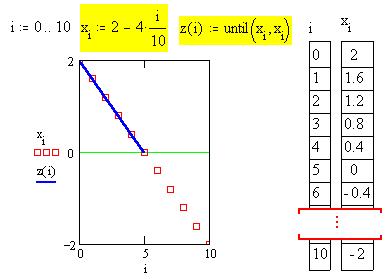
Вернемся опять к понятию массива. В MathCAD
одномерный массив назывется также вектором,
двухмерный - матрицей. Чтобы создать такой
массив, воспользуемся командой Матрицы... из
меню Математика или на панели матричных
операций кнопкой  Появляется диалоговое окно: Появляется диалоговое окно:
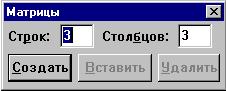
Введем имя матрицы, например А, затем
оператор присваивания и щелкнем по кнопке Создать
:
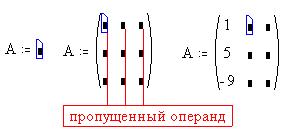
Последовательно перемещаемся по черным
прямоугольникам ввода с помощью клавиши [Tab] и
печатаем значения элементов матрицы .
Рассмотрим некоторые операции с матрицей,
учитывая, что по умолчанию первый номер - нулевой:
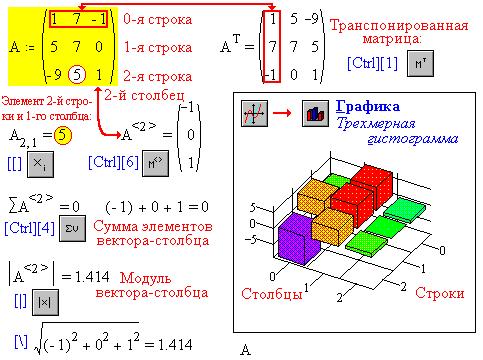
Ясно, что для непосредственного ввода
вектора-столбца в диалоговом окне нужно задать
количество столбцов - 1.
Арифметические действия между числами и
массивами достаточно просты:

Умножение матриц более сложно. Приведем пример единичной
матрицы , такой, что произведение матрицы А на
единичную не меняет А:
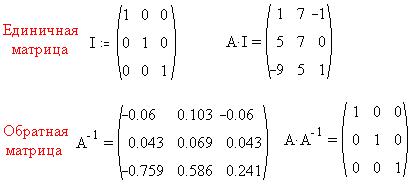
Матричная форма записи удобна для решения в
MathCAD систем линейных уравнений. Ниже х -
вектор-столбец корней системы:

Рассмотрим операции с одномерными массивами -
векторами, причем ограничимся примерами
трехэлементных массивов - трехкомпонентных
векторов для наглядной геометрической
интерпретации:
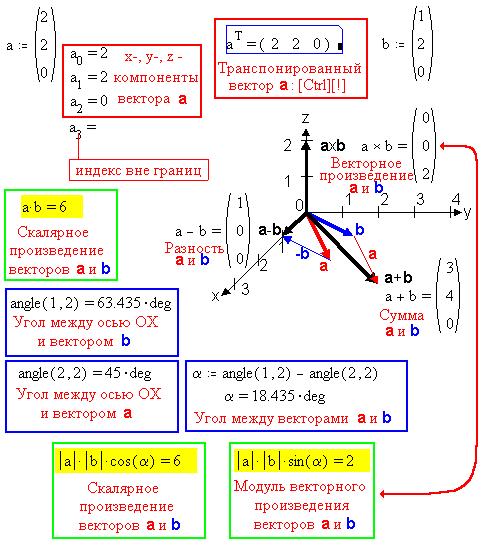
Вектор 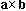 , векторное
произведение, составляет с
векторами-множителями правовинтовую тройку
векторов, как, например, вектор напряженности
поля силы Лоренца, равный векторному
произведению вектора скорости движения
точечного электрического заряда на вектор
индукции магнитного поля: , векторное
произведение, составляет с
векторами-множителями правовинтовую тройку
векторов, как, например, вектор напряженности
поля силы Лоренца, равный векторному
произведению вектора скорости движения
точечного электрического заряда на вектор
индукции магнитного поля: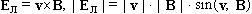
Отметим, что векторная диаграмма создана в MathCAD
как объект приложения Visio Express Drawing 3.0,
позволяющего эффективно создавать графические
образы в MathCAD и Microsoft Office, в том числе используя
богатый набор готовых графических форм.
Задавать массивы можно и поэлементно , в
том числе указывая не полностью весь массив, -
MathCAD заменит недостающие элементы нулями:
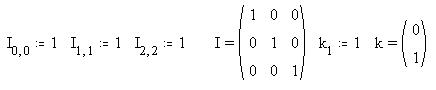
Выделив элемент массива (на примере ниже
это первый элемент созданного массива М0,0
= 1), можно, используя диалоговое окно создания
матриц, ниже и правее этого элемента вставить
нужное число строк и столбцов, а также, начиная со
строки и столбца, на пересечении которых
находится выделенный элемент, удалить указанное
число строк и столбцов:
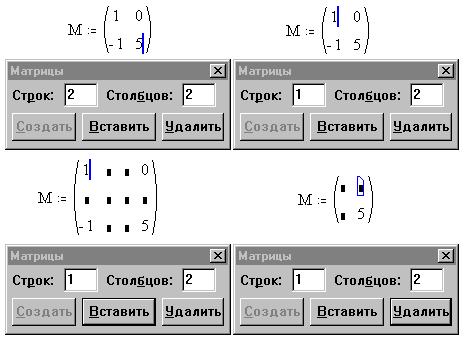
Наконец, массив, размер которого превышает 9
строк или столбцов, MathCAD отображает в виде таблицы
с полосами прокрутки :
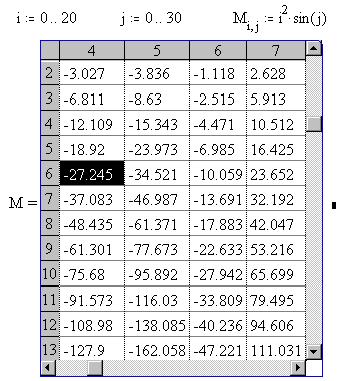
Выделив таблицу пунктирной рамкой , можно
изменять её размер.
Уменьшим размер таблицы и создадим рядом её
образ в форме графика поверхности:
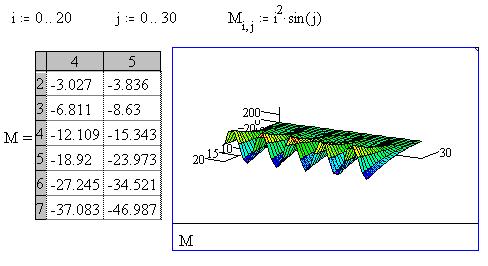
Отметим также возможность выделения и
копирования какой-либо части табличных данных
для вставки в другую область рабочего документа
(а также в другое приложение Windows).
Рассмотрим две встроенные функции, позволяющие
вывести число элементов вектора и поменять
порядок элементов на противоположный, в задаче
составления из элементов вектора десятичного
числа:

Оператор суммирования по степеням основания
системы счисления вставляется кнопкой  панели символов или
клавишами [Ctrl][Shift][4] . панели символов или
клавишами [Ctrl][Shift][4] .
Кроме обращения порядка элементов вектора
можно обратить порядок строк матрицы, а также
сортировать (расположить по возрастанию
элементов) как вектор, так и любые строку или
столбец матрицы:

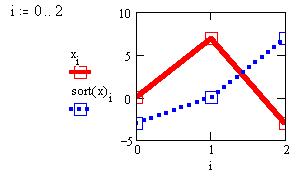
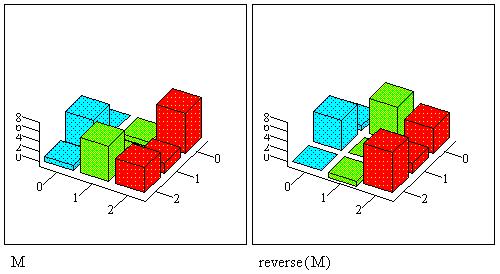
Результат действия встроенных функций
сортировки элементов вектора и обращения
порядка строк матрицы отобразим на графиках:
MathCAD позволяет кроме десятичного представления
чисел (по умолчанию) использовать шестнадцатеричный
и восьмеричный форматы: при вводе константы
за последней цифрой печатаем латинские буквы Н
или О (независимо от регистра). Аналогично
использованию этих встроенных констант
вводим и встроенные единицы измерений :

Вернемся к знакомству со встроенными функциями
для нахождения корня уравнения. Встроенная
функция root(f(x),x) (root - корень) при
предварительном вводе начального приближения
корня возвращает ближайшее к приближенному
значение х, при котором выражение f(x)
обращается в нуль.
Если выражение f(x) имеет вид полинома
типа 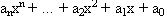 , то
удобнее использовать встроенную функцию polyroots(v),
которая для указанного вектора коэффициентов
полинома начиная с константы возвращает вектор
всех корней (без предварительных приближений): , то
удобнее использовать встроенную функцию polyroots(v),
которая для указанного вектора коэффициентов
полинома начиная с константы возвращает вектор
всех корней (без предварительных приближений):
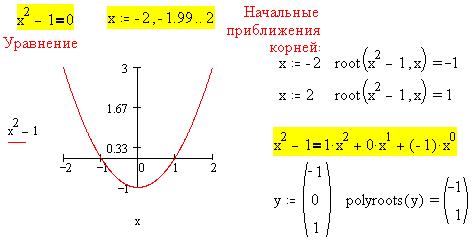
Используя встроенную функцию root(f(x),x)
рассмотрим простейший способ решения уравнения
с параметром . Для этого определяем функцию
двух переменных - от параметра и от неизвестной
уравнения, вычисляющую при заданном приближении
корень уравнения для каждого значения параметра:
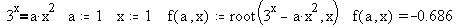
Создадим целочисленный массив значений
параметра а в уравнении предыдущего примера и
определим массив решений уравнения для каждого
значения параметра:

Перейдем теперь к нахождению корней системы
уравнений. Заметим, что максимальное число
уравнений (и переменных) равно 50 (минимальное - 1). При
предварительно указанных начальных
приближениях корней ключевое слово Given (дано,
- формат шрифта - любой) указывает MathCAD, что далее в
документе следуют уравнения системы, правая и
левая части которых разделены символом логического
равенства [Ctrl][=] (система может включать и неравенства
ограничений с соответствующими символами
неравенств). После этого встроенная функция Find(x,y,...)(Find
- найти) возвращает вектор решений:
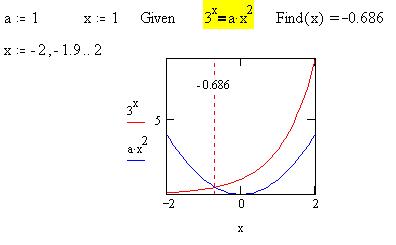
Найдем теперь координаты точки пересечения
окружности и прямой на плоскости. Предварительно
построим график, используя отдельную переменную
z, чтобы "не мешать" работе встроенной
функции:
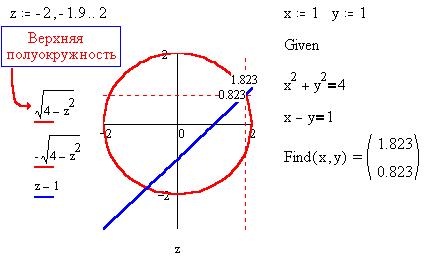
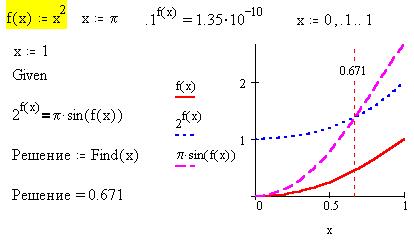
Найдем координаты одной из точек пересечения
параболы и синусоиды с теми же значениями z, что и
выше, используя при системе уравнений ограничительное
неравенство x<0:
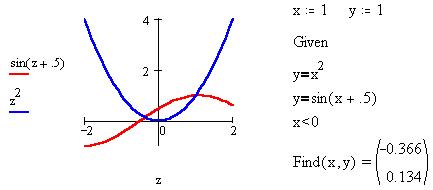
Обратим внимание, что пользователь
"вправе" определять собственные функции,
которые можно использовать и для графических
представлений, и для вычислений, в том числе для
нахождения корней системы уравнений:
Ранее мы уже находили символьное решение
уравнения движения. Приведем еще ряд примеров
символьного решения уравнений и их графики.
Напомним, что в отсутствие логического
(полужирного) знака равенства либо иного
логического оператора MathCAD приравнивает
введенное выражение нулю. Решения находим,
выделив переменную, командой Решить относительно
переменной из меню Символика :
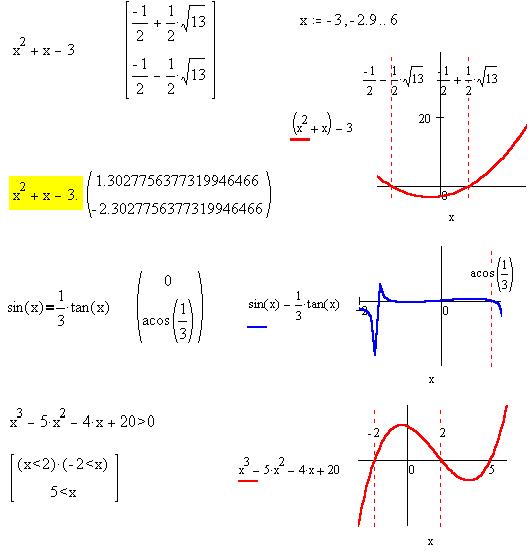
Отметим, что в подсвеченном выражении нами
использована десятичная точка при записи числа 3,
в результате чего при символьном вычислении
выражение с иррациональным числом 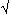 13 получает десятичную
аппроксимацию с 20 значащими цифрами (по
умолчанию). 13 получает десятичную
аппроксимацию с 20 значащими цифрами (по
умолчанию).
В ответе последнего примера использовано
логическое умножение:(x<2) И (-2<x).
Расположение ответа устанавливается в
диалоговом окне, вызываемом командой
Расположение результата... в меню Символика.
Например, в первых трех примерах расположение
ответа горизонтально (справа от выражения),
а в последнем примере расположение вертикально,
вставляя строку. Команда Замещать в том
же меню приводит к замещению введенного
выражения результатом символьных вычислений
(выражение при этом пропадет).
Символьные преобразования введенного и выделенного
полностью синей рамкой выражения (в т. ч.
нахождение численного результата) вызываются
командой Вычислить в символах (клавиши [Shift][F9])
меню Символика :
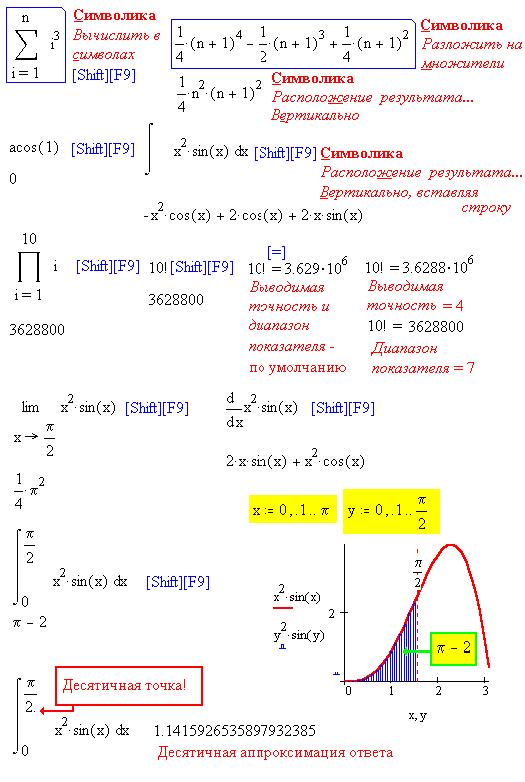
Площадь под кривой выражается иррациональным
числом  - 2, десятичная
аппроксимация которого с 20 значащими числами
вызвана использованием десятичной точки при
вводе числа 2. - 2, десятичная
аппроксимация которого с 20 значащими числами
вызвана использованием десятичной точки при
вводе числа 2.
Отметим также погрешность при обычном, "не
символьном" вычислении факториала 10.
Команда Упростить из меню Символика выполняет
основные алгебраические и тригонометрические
преобразования выделенной части выражения
(в частности, если всё выражение не упрощается). В
некоторых случаях результат упрощения просто
совпадает с результатом символьного вычисления:

Команда Разложить по степеням из меню Символика
в выделенном полностью выражении разлагает
степени и произведения сумм, числители дробей
(выражение представится как сумма дробей).
Тригонометрические функции сложного аргумента
будут разложены в выражения, включающие только
синусы и косинусы одиночных переменных :

Команда Разложить на множители из меню Символика
разлагает выделенную часть выражения (при
трудностях выделения следует выбранную часть заключить
в скобки и щелкнуть по скобке). Целое число
будет представлено произведением степеней
простых чисел :

Приведение подобных членов (выделяется переменная
либо встроенная или введенная
пользователем функция вместе с аргументом)
объединяет члены, содержащие одинаковые степени
выделенного выражения по команде Разложить по
подвыражению из меню Символика :

Рассмотрим теперь порядок замены переменной на
скопированное ранее выражение :
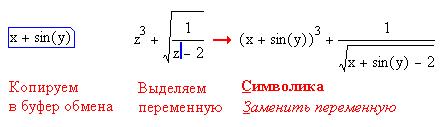
В меню Символика содержатся также
команды символьных преобразований матриц Транспонировать
и Обратить. Создадим матрицу из элементов
а00 ... а11 , определив предварительно их
численные значения:
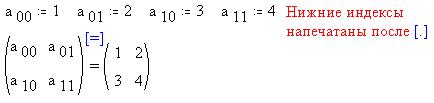
Теперь рассмотрим результаты символьных
преобразований, а также получим численные
значения, нажимая всякий раз в конце
преобразования на клавишу [=]:
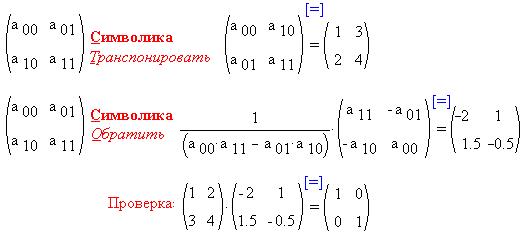
Воспользуемся возможностями символьных
преобразований для получения формул абсолютной
и относительной погрешностей косвенных
измерений на примере косвенного измерения
удельного сопротивления материала тонкого
провода.
Согласно закону Ома и определению удельного
сопротивления r проводника найдем расчетную
формулу:
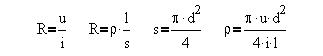
В формулу входят непосредственно измеряемые
приборами физические величины: u - напряжение, i -
сила тока, l - длина провода, d - диаметр провода.
Пусть также известны абсолютные погрешности
прямых измерений .jpg) u, u, .jpg) i, i, .jpg) l, l, .jpg) d. Для нахождения формулы
абсолютной погрешности косвенного измерения
можно использовать формулу полного
дифференциала относительно конечных
погрешностей прямых измерений: d. Для нахождения формулы
абсолютной погрешности косвенного измерения
можно использовать формулу полного
дифференциала относительно конечных
погрешностей прямых измерений:
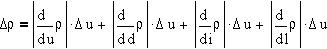
Модули частных производных найдем с помощью
символьных вычислений:
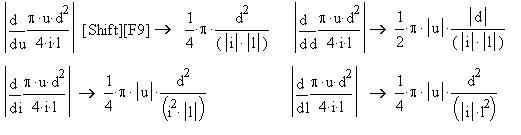
Теперь отредактируем полученные результаты: удалим
прямые (да и круглые) скобки. Формула абсолютной
погрешности довольно громоздкая:
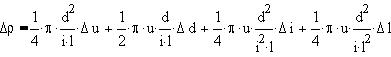
Найдем более компактную формулу относительной
погрешности как отношение выражения для
абсолютной погрешности к выражению для
удельного сопротивления:
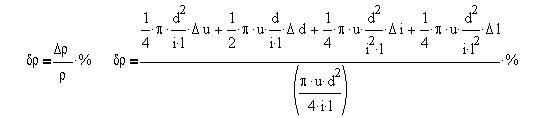
Выделив правую часть выражения, выберем в меню Символика
команду Разложить по степеням . Получим
результат сокращений:
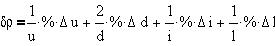
Как видим, относительная погрешность
косвенного измерения определяется
относительными погрешностями прямых измерений,
причем, заметим, процент ошибки измерения
диаметра провода входит в формулу удвоенным:
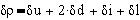
Пусть, например, мы однократно измерили диаметр
штангенциркулем . Абсолютнная погрешность
измерения равна инструментальной погрешности и
составляет 0,05 мм. Пусть также измеренный диаметр
равен 0,5 мм. Тогда измерение диаметра
штангенциркулем внесло в общую относительную
погрешность 20%:
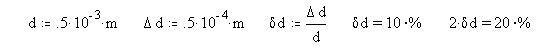
Ясно, что для измерения диаметра тонкой
проволоки придется найти микрометр , что
уменьшит процент вносимой ошибки в 10 раз.
Итак, символьные преобразования позволили,
во-первых, легко найти формулы погрешностей
косвенного измерения величины, зависящей от 4
переменных, и, во-вторых, еще до прямых измерений
оценить методику эксперимента.
2. От базовой версии- к профессиональной
Профессиональная версия MathCAD 6.0 PLUS отличается
от базовой рядом дополнительных возможностей и
удобств для пользователя.
В области символьных вычислений это, во-первых,
символьный знак равенства "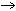 ", возвращающий не только число, но и
выражение. Для его действия необходимо выбрать
команду Использовать символику при
помеченной команде Автоматический режим
(вычислений) в меню Математика : ", возвращающий не только число, но и
выражение. Для его действия необходимо выбрать
команду Использовать символику при
помеченной команде Автоматический режим
(вычислений) в меню Математика :
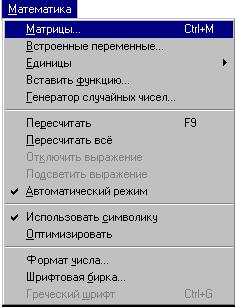
Напомнимим, что автоматический режим
отображается на панели инструментов кнопкой с
горящей лампочкой: 
После введенного выражения набираем
комбинацию клавиш [Ctrl][.], затем [Enter]
:
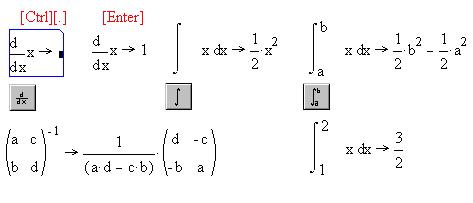
По умолчанию при этом выполняется операция Вычислить
в символах ([Shift][F9]) из меню Символика,
но если предварить выражение специальным ключевым
словом , то будут выполняться и другие команды
меню, как это видно из рисунка ниже (в сущности,
указанные команды - дословный перевод английских
наименований соответствующих математических
преобразований, которые и являются ключевыми
словами):
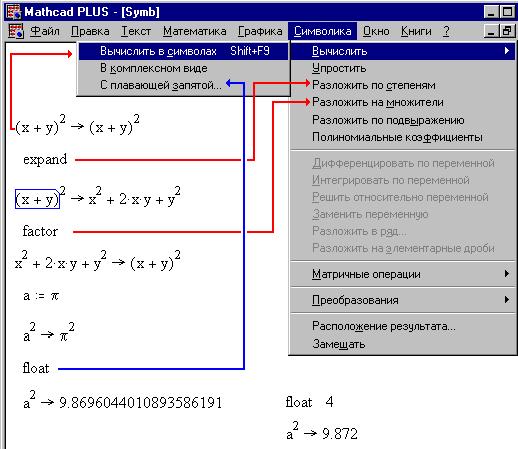
В последнем примере число "4", напечатанное
правее ключевого слова "float", означает
четыре значащих цифры в вычисляемом с плавающей
запятой результате.
На примере ниже видно, что ключевое слово
"assume" приводит к игнорированию численного
значения соответствующей переменной:
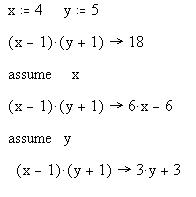
Во вторых, особенностью профессиональной
версии является вычисление сложных выражений в режиме
оптимизации (команда Оптимизировать из
меню Математика): предварительно такое
выражение оптимизируется, т. е. как бы
подвергается последовательно двум символьным
операциям - разрешению в символах и затем упрощению
, а вычисление уже производится над полученным
простым выражением.
Найдем сумму квадратов целых чисел от 1 до 100.
Получим сначала (в два этапа) упрощенную простую
формулу. Потом найдем численный результат
напосредственно. А затем применим режим
оптимизации только к одному выражению с помощью
ключевого слова "optimize": рядом с ним появится
красная звездочка, двойной щелчок мыши по
которой открывает окно с результатами
символьного упрощения, при этом дальнейший
расчет производится именно по найденной формуле,
т. е. наиболее эффективно:

В-третьих, в профессиональной версии есть
возможность символьного решения систем
уравнений .
Если после такого решения системы в общем виде
ввести численные значения соотвествующих
переменных, то, скопировав столбец формул в буфер
обмена и затем вставив его после определения
переменных, оператором "=" получаем
численные значения корней системы, имеющих
геометрический смысл координат точек
пересечения кривых. В примере ниже - это точки
пересечения окружности и прямой:
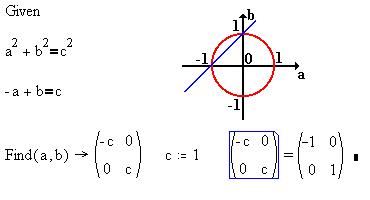
Программирование в MathCAD 6.0 PLUS.
В профессиональной версии MathCAD 6.0 PLUS существует
возможность определить функцию, используя не
один, а несколько операторов, и тем самым
определить функцию не выражением, а
программой .
На панели символов встроена палитра
программирования :
Рассмотрим два способа задания
кусочно-непрерывной функции:
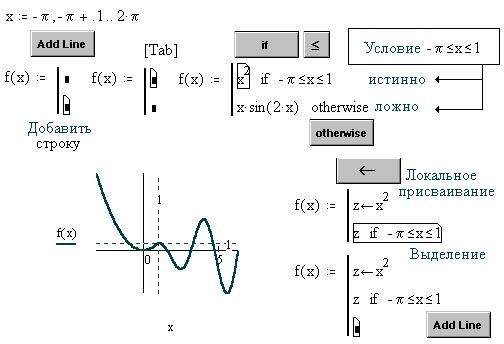
Оператор Add line создает справа от линии
столбец строк для ввода операторов; if (если)
- условный оператор: выражение f(x) принимает
значение слева от if, если условие справа
истинно; слева от оператора otherwise (иначе)
введено значение, которое принимает выражение
f(x), если условие справа от if ложно.
Оператор локального присваивания 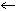 присваивает внутри
программы , локально переменной слева
значение справа от оператора. присваивает внутри
программы , локально переменной слева
значение справа от оператора.
Операторы while (пока) и for (для)
позволяют организовать циклические процессы
вычислений, а оператор break дает
возможность выхода из цикла.
3. HELP! - работа со справочной системой
MathCAD
Справочная поддержка пользователя MathCAD
многовариантна: кроме всплывающих подсказок,
возникающих при наведении указателя мыши на
элементы управления окном (кнопки панелей и т. п.),
кратких сообщений в строке соообщений внизу
окна и сообщений об ошибках (в красной рамке)
в меню ? выполняются следующие команды
справочной службы:
Команда Индекс открывает типовое окно
Справки Windows-приложений:
Щелчком по кнопке слева от нужного раздела
открываем соответствующую справку. Выбрав
кнопку-команду Содержание, открываем окно
со понятийным списком, передвигаться по которому
можно как с помощью полос прокрутки, так и
напечатав несколько букв имени нужного понятия:
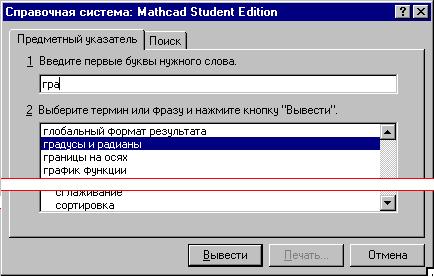
Выведем, например, раздел справки
"градусы и радианы", отмеченный на рисунке
выше:
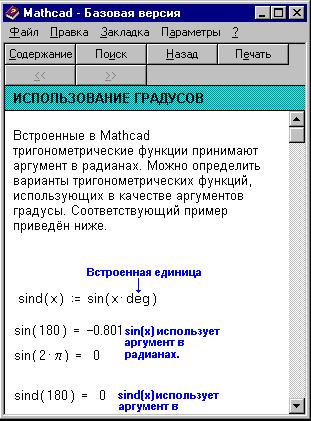
Открыв закладку Поиск , получаем
дополнительные возможности поиска нужного
термина.
Вызвать раздел справки, относящийся к элементу
документа или окна MathCAD можно после нажатия
комбинации клавиш [Shift][F1] (справа от
белой стрелки - указателя мыши указателя мыши
появится черный вопросительный знак) щелчком по
нужному элементу. Вызовем таким образом контексную
справку , например, по кнопке создания
текстовой области:
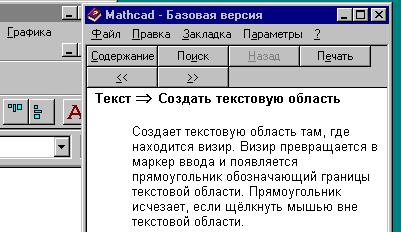
Команда Техническая поддержка... меню ?
вызывает ответы на вопросы, связанные с
техническими проблемами пользователя.
Команда Шпаргалки меню ?
открывает гипертекстовую электронную книгу
, состоящую из готовых файлов - примеров MathCAD,
которые можно непосредственно редактировать
(при этом информация в них защищена от изменений,
- изменения не сохраняются при закрытии
шпаргалки), а также переносить в свой документ:
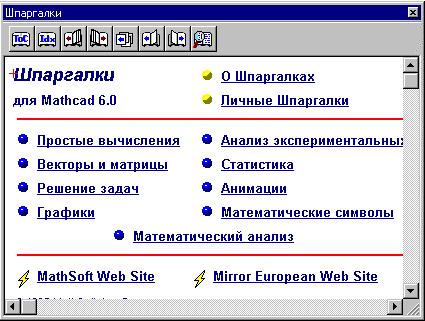
Откроем двойным щелчком мыши гиперссылку из
раздела "Графики":
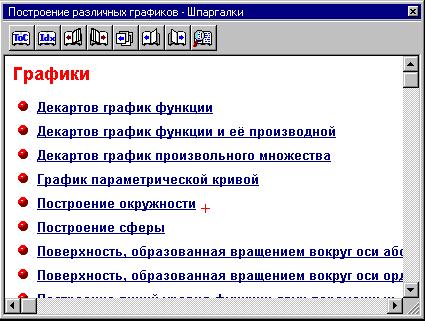
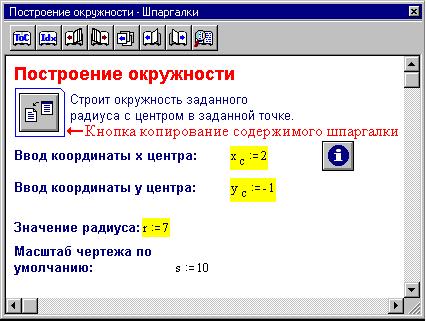
Точно так же откроем раздел "Построение
окружности", выделим пунктирной рамкой
рабочие области документа-примера и перетащим
мышью в свой документ:
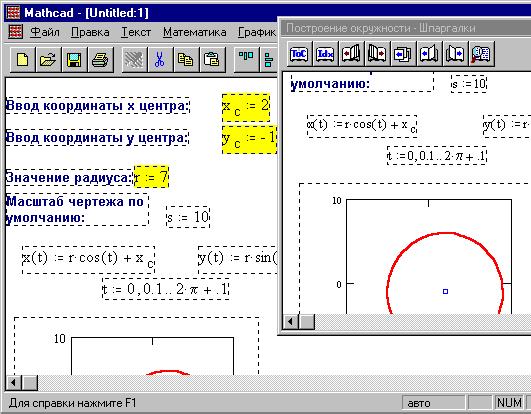
Аналогичный результат можно получить, вставив
скопированные в буфер обмена выделенные области
шпаргалки либо, после двойного щелчка по специальной
кнопке шпаргалки, двойным щелчком по своему
документу: первое действие копирует весь
пример в буфер обмена, второе - вставляет
скопированное. Указатель мыши при этом примет
вид стрелки с книгой.
Команда Открыть книгу... меню Книги дает
доступ к имеющимся электронным книгам,
устроенным аналогично шпаргалкам.
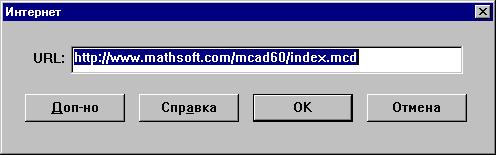
Доступ к готовым файлам MathCAD, расположенных на
Web-серверах разработчика MathCAD - фирмы MathSoft (MathSoft,
Inc. USA), вызывается командой Интернет меню Файл:
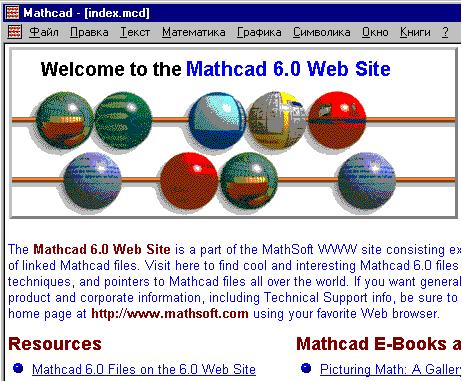
Вид Web-страницы фирмы MathSoft:
Содержание
Вернуться на страницу
<Методические разработки> |

