Вернуться
на страницу <Методические разработки>
Содержание
MathCAD 6.0: практическое пособие для
старшеклассников
Настоящее пособие отражает опыт работы
сотрудников МГДТДиЮ, МИРЭА, школ и межшкольных
учебных комбинатов по внедрению средств НИТ в
непрерывный образовательный процесс. Оно
ориентировано как на систему дополнительного
образования (учебно-творческие коллективы в
сфере НИТ, радиотехники, электроники и
электротехники), так и на систему общего
образования (компьютерная поддержка курсов и
практикума по физике, математике, информационным
технологиям). Материалы могут быть использованы
для дистанционного образования, в т. ч.
учащихся-инвалидов.
Учебный процесс на автоматизированном рабочем
месте (АРМ) учащихся, включающем ПЭВМ и
позволяющем использовать MathCAD 6.0, ставит
качественно новую задачу использования
элементов классической математики при изучении
соответствующих разделов физики и
профориентационных общетехнических дисциплин.
Цель предлагаемого учебного пособия -
эффективное практическое усвоение учащимися
старших классов основных возможностей базовой
версии MathCAD 6.0, а также знакомство с
профессиональной версией.
Электронная версия пособия готовится к
размещению на WWW-серверах МГДТДиЮ и МИРЭА в
разделе "Программно-методические фонды в
сфере НИТ".
Часть 1. Гонка за лидером: практическое
введение в MathCAD 6.0 BASIC
Итак, открываем MathCAD 6.0 Basic. Появляется заставка

и окно :
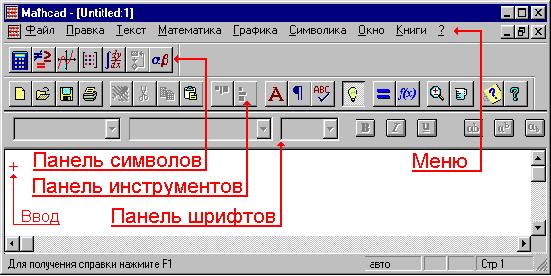
Все три панели кнопок можно закрыть
(либо открыть снова) командами из меню Окно
. Красный крестик показывает место создания
(ввода с клавиатуры либо командами из меню или
панелей) новой области: формулы, текста,
рисунка и пр. Области располагаются, как на
обычном листе бумаги - в произвольном порядке (с
той лишь разницей, что численные значения
переменных и функции, определенные ранее,
должны быть расположены левее или выше
области их использования). Крестик
устанавливается щелчком мыши либо клавишами со
стрелками на клавиатуре.
Кнопки на панелях служат для выбора с помощью
мыши команд, содержащихся в меню, а также
математических символов (операторов ) и букв
греческого алфавита. Ясно, что и команды, и
символы, и греческие буквы можно вводить с
клавиатуры, причем зачастую это более удобно.
Знакомство с панелями кнопок начнем с панели
символов, для чего щелчком мыши по кнопкам
раскроем палитры символов :
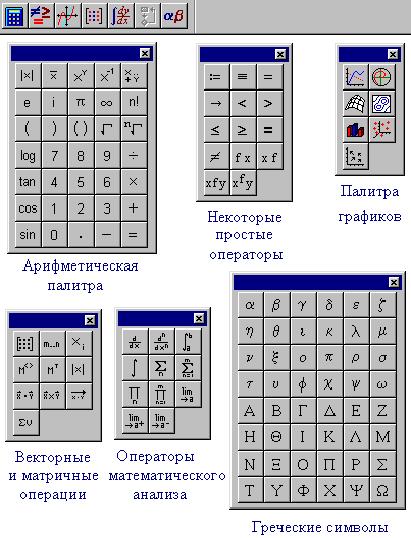
Чтобы узнать название любой кнопки на панелях
или палитрах, достаточно навести на кнопку
курсор мыши: появится всплывающая подсказка
с названием. В дальнейшем тексте будут
использоваться и название кнопок, и их
изображение.
Теперь, когда все кнопки видны, приступим к
практическим действиям: попробуем применить
возможности MathCAD для решения задачи по курсу
физики 9 класса о равноускоренном движении
материальной точки.
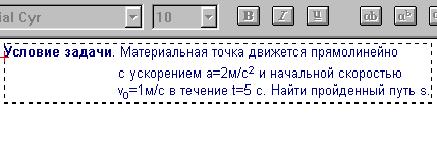
Вначале создадим в нашем электронном
документе текст условия задачи, для чего выберем
команду Создать текстовую область в меню Текст
, либо на клавиатуре выберем кавычку ["], либо
щелкнем на панели инструментов по кнопке: 
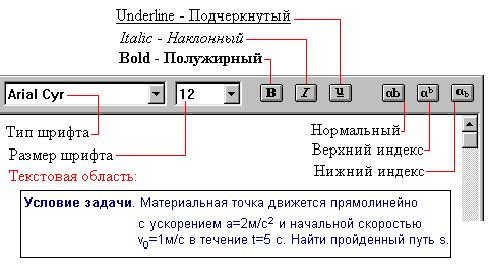
Текстовая область имеет форму прямоугольника,
размеры которого определяются конфигурацией
текста по желанию пользователя. Выделив при
нажатой левой кнопке мыши либо клавишей
клавиатуры для перемещения курсора при нажатой
клавише [Shift] часть текста, на панели шрифтов
задаем его характеристики, как на рисунке выше.
Это же можно сделать, выбрав команду Изменить
шрифт в меню Текст, в диалоговом окне форматирования
(в нем показываются параметры шрифта,
установленные по умолчанию ):
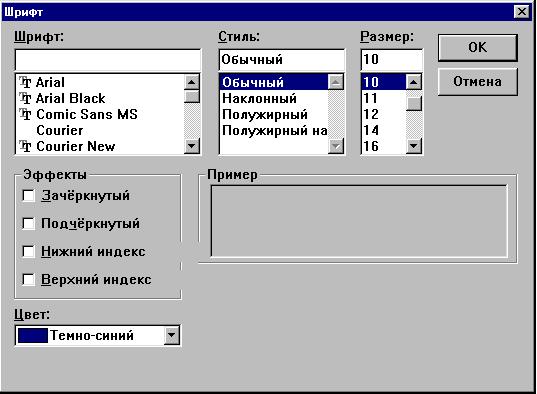
Чтобы изменить характеристики шрифта по
умолчанию, воспользуемся командой Изменить по
умолчанию и, далее, Шрифт в меню Текст
в таком же диалоговом окне.
Нажав вне области левую кнопку мыши и не
отпуская ее, переместим курсор на область, чтобы
она выделилась пунктирным прямоугольником:
Отпустим кнопку. Теперь внутри области форма
курсора - черный крестик, и, нажав кнопку мыши,
можно перетаскивать область в любое место
документа. Снимаем выделение, щелкнув мышью вне
области
Можно также создать текстовый параграф,
занимающий всю строку документа: команда Создать
текстовый параграф в меню Текст ,
либо комбинация клавиш [Ctrl][T], либо на панели
инструментов кнопка: 
Изменим конфигурацию текстовой области, вводя
новые строки с помощью клавиши ввода [Enter], и
создадим рисунок к задаче как объект
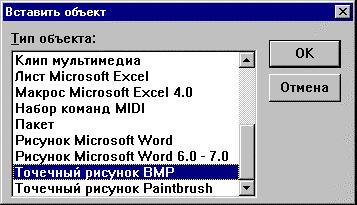
графического редактора Paint, для чего в меню Правка
выберем команду Вставить объект... В
появившемся диалоговом окне выбираем опцию
Точечный рисунок ВМР :
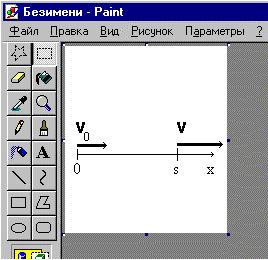
Теперь с помощью инструментов редактора
создаем простой чертеж
Закрывая окно Paint, тем самым вставляем объект в
документ MathCAD (для повторного вызова средств
графического редактора и редактирования чертежа
достаточно сделать двойной щелчок мышью по
объекту):
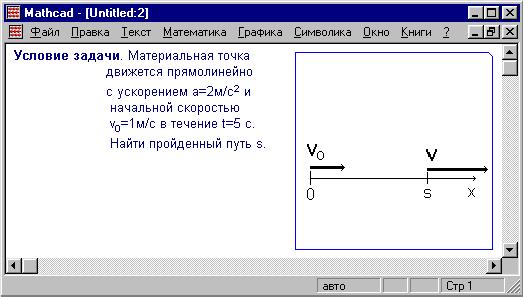
Рамка выделения синего цвета не позволяет перетаскивать
или удалить объект. Для этих действий нужно
выделить его пунктирной рамкой .
Перед тем, как заняться вычислениями, сохраним
документ, а затем, создав новый для вычислений, вставим
в этом новом документе гиперссылку на файл с
условием задачи и чертежом с тем, например, чтобы
они не занимали место в расчетном документе.
Для сохранения документа выберем команду Сохранить
как в меню Файл и в диалоговом окне
создадим новую папку "Problem", где будем
хранить файлы с условиями задач:
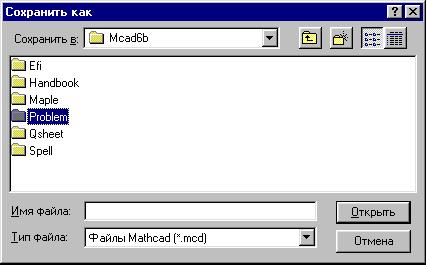
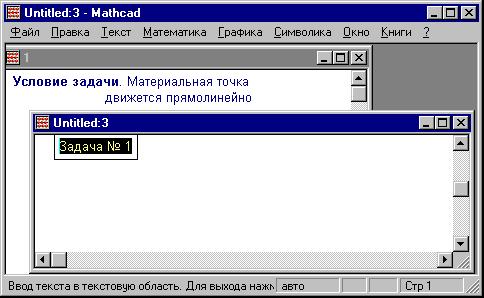
Файл сохраним под именем 1.mcd и, не закрывая
его, создадим новый , в котором напечатаем
текст для гиперссылки, например, "Задача №
1", выделив этот текст:
Выберем затем команду Связь Новая в меню Правка
и в диалоговом окне укажем на файл 1.mcd:
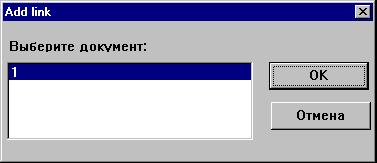
Здесь Add link дословно означает Добавить
связь .
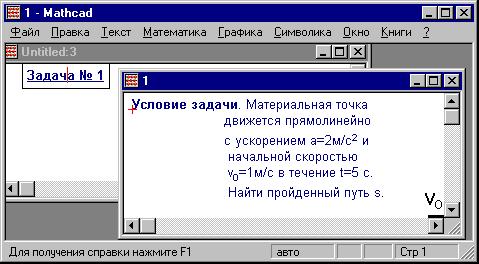
Теперь файл с условием задачи можно закрыть и в
любой момент вызвать двойным щелчком по
выделенному тексту (шрифт полужирный,
подчеркнутый ) гиперссылки:
Таким образом, гипертекст создает
возможность многократного использования
документов и мультимедийных объектов (тексты,
графика, аудио- и видеоклипы), не перегружая ими
свои рабочие файлы. Одновременно открыть и
создать гиперсвязь можно с 8 файлами MathCAD, в т. ч.
размещенными на каких-либо серверах Интернет.
Связь может быть создана не только с частью или
всей текстовой областью (что предпочтительней в
силу заметного шрифтового выделения), но и с
формулой или графиком. Недостатком здесь будет,
во-первых, отсутствие выделения и, во-вторых,
невозможность форматирования областей с помощью
двойного щелчка мыши. Устранить связь позволяет
выбор команды Связь Удалить из меню Правка.
Если изменить адрес связанного файла, то,
естественно, связь станет невозможной. Наконец, Справка
(меню ?, клавиша [F1] либо кнопка  ), а также электронные
книги (Шпаргалки) с готовыми примерами
(команда Открыть книгу в меню Книги
или кнопка ), а также электронные
книги (Шпаргалки) с готовыми примерами
(команда Открыть книгу в меню Книги
или кнопка  )
устроены на гиперссылках. )
устроены на гиперссылках.
Перейдем вычислениям.
Формула для расчета пути известна: 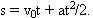 Подставим сразу численные
значения: Подставим сразу численные
значения:
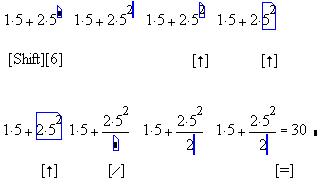
На третьем, четвертом и пятом шагах клавишей [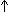 ] мы выделили группу
множителей, чтобы образовать из них единый
числитель "как в формуле". Аналогично
действует и клавиша "Пробел" [Space]. Клавиша [ ] мы выделили группу
множителей, чтобы образовать из них единый
числитель "как в формуле". Аналогично
действует и клавиша "Пробел" [Space]. Клавиша [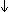 ], наоборот, уменьшает синюю
рамку выделения. Клавиши [ ], наоборот, уменьшает синюю
рамку выделения. Клавиши [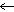 ],
[ ],
[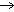 ] перемещают синюю рамку
выделения на "соседа по математическому
действию". ] перемещают синюю рамку
выделения на "соседа по математическому
действию".
Итак, MathCAD превращает лист тетрадки в
суперкалькулятор.
Теперь решим задачу более тщательно: введем имена
переменных и присвоим им численные
значения, а также введем формулы для
нахождения значений переменных.
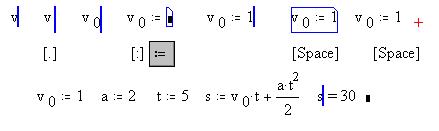
Как видим, нижний индекс в имени
переменной записывается, начиная с [.]. Оператор
присваивания := - кнопка палитры или [:]. Введя
значение переменной v0, мы дважды
нажали клавишу "Пробел": сначала все
выражение выделилось синей рамкой, а затем место
ввода - красный крестик стал на ближайшую
позицию в этой же строке. Так компактнее и
аккуратнее. Хотя можно, натянув "паутинку" -
пунктирную рамку выделения на несколько
областей, выровнять их по горизонтали (по
вертикали) командой Выровнять области
Горизонтально (Вертикально) в меню Правка.
Можно также расположить области строго по
вертикали, "столбиком", нажимая после ввода
каждой клавишу [Enter]. Комбинации клавиш
[Shift][Стрелка] выводят крестообразный курсор из
вводимого выражения влево (вправо) в строке или
вверх (вниз) в столбце . Без [Shift] клавиши стрелок
перемещают, как уже замечалось, рамку выделения
или (клавиши [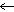 ],[ ],[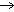 ]) перемещают маркер ввода
по выражению, которое при этом редактируется, как
обычный текст. ]) перемещают маркер ввода
по выражению, которое при этом редактируется, как
обычный текст.
Рассмотрим ограничения на имена переменных:
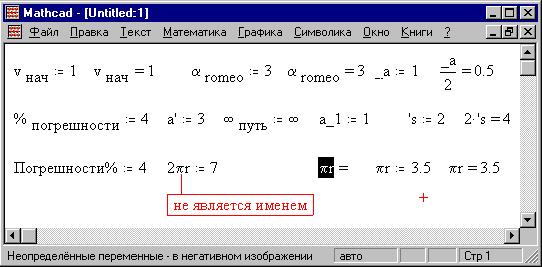
Алфавит - английский, греческий, русский (все
буквы - в том же начертании; верхний и нижний
регистры (строчные - прописные) различаются).
Греческие буквы - из палитры инструментов либо
после ввода "похожей" латинской буквы
комбинация клавишей [Ctrl][g]. Буква  - сразу [Ctrl][p]. - сразу [Ctrl][p].
Используется нижний индекс (вводится после [.],
"понижающей" маркер ввода).
Используются цифры, знак подчеркивания [_],
"левый" штрих [`], знак [%] и знак бесконечности
[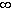 ]. Цифра не может быть
первой в имени, а знак [ ]. Цифра не может быть
первой в имени, а знак [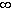 ] не
первым (его не первым и не ввести). Не
рекомендуется также первыми в имени переменной
вводить знаки [_],[`] и [%], хотя, как это видно на
рисунке, такие имена "принимаются". ] не
первым (его не первым и не ввести). Не
рекомендуется также первыми в имени переменной
вводить знаки [_],[`] и [%], хотя, как это видно на
рисунке, такие имена "принимаются".
При выводе значения не определенной левее
или выше (MahtCAD "читает" документ
по-европейски: слева - направо и сверху - вниз)
переменной ее имя выделяется в негативном
изображении.
Наконец, не нужно бояться ясных, но длинных
имен: выделим имя синей рамкой, скопируем в
буфер обмена (команда Копировать в меню Правка
либо клавиши [Ctrl][c]), затем щелкнем в нужном месте
документа и вставим имя (команда Вставить
в меню Правка либо клавиши [Ctrl][v]).
Выделять для копирования можно и пунктирной
рамкой.
В MathCAD есть и так называемые предопределенные
переменные , значения которых установлены по
умолчанию, например:
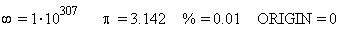
В данном документе можно переопределить
их значения. Скажем, номер первого элемента
массива чисел (таблицы) - ORIGIN ("начало") -
можно сделать равным 1:
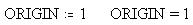
Теперь замечание по числам. Десятичные дроби
записываются с десятичной точкой.
Выводимую точность (количество десятичных
разрядов после точки) можно изменять от 0 до 15.
Числа выводятся в форме представления с плавающей
точкой , если число больше 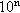 или меньше или меньше 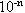 , где n -
целое число, показатель при 10 в экспоненциальном
представлении. Выводимая точность и диапазон
показателя локально (в данном выражении) или глобально
(везде в документе) устанавливается в диалоговом
окне, вызываемом двойным щелчком мыши по числу
или командой Формат числа в меню Математика
: , где n -
целое число, показатель при 10 в экспоненциальном
представлении. Выводимая точность и диапазон
показателя локально (в данном выражении) или глобально
(везде в документе) устанавливается в диалоговом
окне, вызываемом двойным щелчком мыши по числу
или командой Формат числа в меню Математика
:
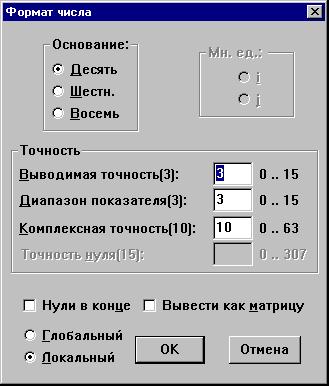
Как видим, по умолчанию выводимая точность
равна трем десятичным разрядам после точки и
диапазон показателя равен 3 ( 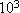 =1000). Определим переменную а:=123.123456789. Трижды
выведем ее значение: сначала с форматом числа по
умолчанию, потом выводимую точность установим
равной 15 и затем диапазон показателя установим
равным 1 ( =1000). Определим переменную а:=123.123456789. Трижды
выведем ее значение: сначала с форматом числа по
умолчанию, потом выводимую точность установим
равной 15 и затем диапазон показателя установим
равным 1 ( 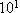 =10). Результаты,
соответственно, следующие: =10). Результаты,
соответственно, следующие:
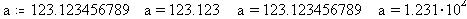
Вернемся к нашей задаче. В ней не приходится
беспокоиться о формате чисел и об именах
переменных. Единственное, что безусловно
огорчило бы учителя физики, так это - неуказанная
размерность физических величин. Для ввода
размерности нужно после ввода численного
значения напечатать оператор умножения, а затем,
выбрав команду Единицы Вставить единицы из
меню Математика, выбрать размерность
и единицу измерений в диалоговом окне
"Вставить единицы". Впрочем, вместо вставки
можно просто напечатать известную единицу
измерений, как если бы это было имя переменной:
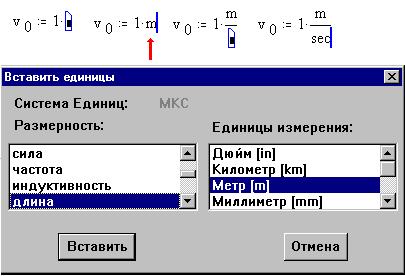
Вот результат: MathCAD "сам" подставил единицу
длины к значению s:
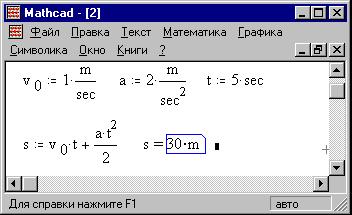
Обратите внимание на место ввода (черный
прямоугольник) единиц измерений на
выделенном выражении s: сюда можно вписать
переменную, константу или выражение, и тогда
результат будет масштабирован в
соответствии с величиной вписанного. В
отсутствие прямоугольника имя размерности можно
просто отредактировать. Если, например, ввести
туда km (километры), то ответ будет таким: 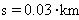
Найдем, например, величину угла, синус которого
равен 0.5:
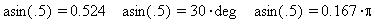
По умолчанию ответ - 0.524 рад; вписав deg (degree -
градус) в место ввода размерности, получили 30
градусов. Или, вписав  ,
получим 0.167 ,
получим 0.167  рад. рад.
В текст MathCAD можно внедрить "живые"
формулы (команда Внедрить формулы в меню Текст),
которые будут автоматически пересчитывать любые
изменения. Их же (как и любое математическое
выражение в документе) можно отключить (команда Отключить
выражение в меню Математика ).Запишем
решение нашей задачи, внедрив формулу ответа в
текст:
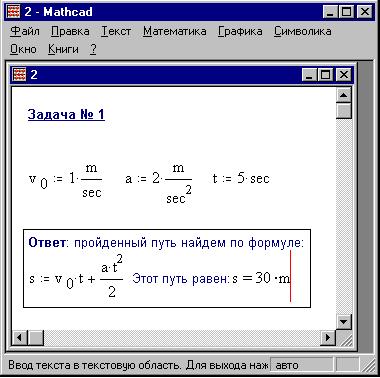
Отключим выражение - формулу пути:
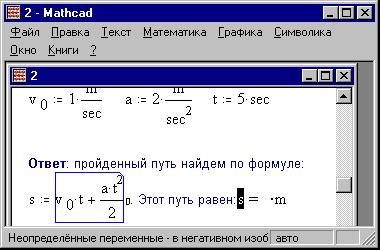
Отключенное выражение отмечено небольшим
прямоугольником справа.
Вспомним теперь о файле 1.mcd с условием задачи и
чертежом. Его можно открыть с помощью
гиперссылки, но его также можно внедрить в
наш расчетный файл 2.mcd командой Внедрить
документ в меню Правка, при этом, как
и при внедрении гиперсвязи, внедряемый файл
должен быть открытым (напомним, что одновременно
можно держать открытыми 8 файлов). Внедренный
документ будет фигурировать в нашем документе в
виде пиктограммы (ярлыка). Двойным щелчком
мыши по пиктограмме (как и при гиперссылке)
внедренный документ будет открыт. Но, самое
главное, все определения внедренного документа
будут выполнятся ниже пиктограммы !
Откроем файл 1.mcd, добавим туда определение
переменной k:=2 и сохраним (Файл Сохранить
либо [F6]). Затом внедрим этот документ в наш
расчетный, выбрав мышью место для пиктограммы
под гиперссылкой:
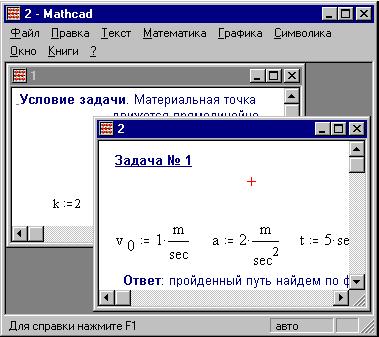
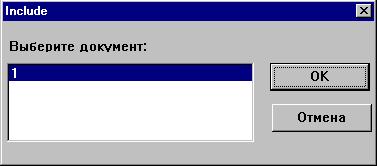
Теперь закроем 1.mcd и вызовем его двойным
щелчком по пиктограмме:
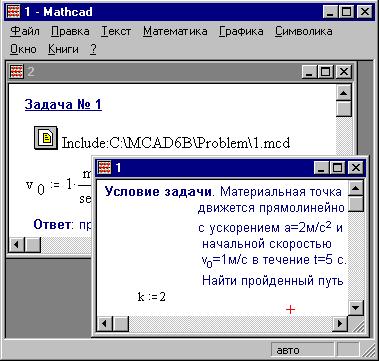
Закроем его опять и проверим "работу" его
определения переменной k в расчетном файле, где
всякое упоминание о ней отсутствует:
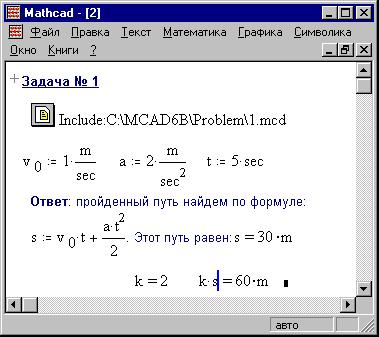
Это и есть "незримое присутствие"
внедренного документа. Как удалить внедренный
документ? Выделить пунктирной рамкой
пиктограмму и удалить (клавиша [Delete] либо команда Очистить
в меню Правка ).
Разумеется, не будем забывать о сохранении
результатов наших действий - [F6].
Кроме рассмотренной технологии внедрения
возможна вставка содержимого другого
документа или целиком всего документа.
В первом случае, открыв другой документ и
выделив в нем пунктирными рамками необходимое
число областей, скопируем их в буфер обмена (Правка
Копировать либо [Ctrl][c], либо кнопка на панели
инструментов), а затем, вернувшись в рабочий
документ и освободив место для вставляемых
областей (например, команда Вст/Удал чистые
строки в меню Правка), вставляем
содержимое буфера обмена (Правка Вставить
либо [Ctrl][v], либо кнопка на панели инструментов).
Выделенные области можно просто перетащить
мышью из одного окна в другое. Тогда при закрытии
уже ненужного документа возможны две ситуации:
- если этот документ был открыт гиперссылкой или
пиктограммой, то "пропажа" областей при
перетаскивании не отразится на содержимом файла;
- если же документ был открыт "обычным"
образом (Файл Открыть), то при
закрытии нужно ответить "Нет" на
предложение компьютера сохранить изменения
, иначе "пропажа" состоится.
Вставляя другой документ целиком (Файл
Вставить документ ) о свободном месте можно
не беспокоиться: области ниже красного крестика
сдвинутся, освободив место для файла. Итак, вот
результат вставки документа 1.mcd в документ 2.mcd
(место вставки, крестик, сразу под гиперссылкой):
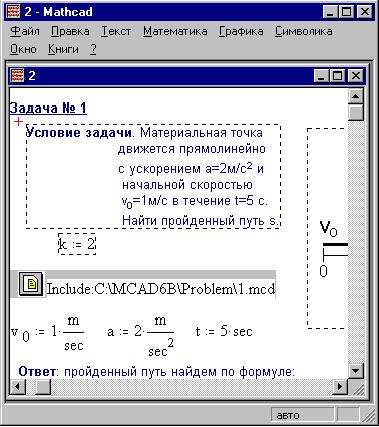
Следует иметь в виду, что вставка и внедрение
возможны из других Windows-приложений в MathCAD и
наоборот, а именно - экспорт и импорт
документов. Так что, например, проведенный в MathCAD
расчет можно вставить в документ Word (как RTF-файл),
а документ Word можно внедрить в документ MathCAD.
Кроме вычислений MathCAD способен
производить аналитические, или, по принятой
терминологии, символьтные преобразования
математических выражений (меню Символика
).
Рассмотрим для примера нашу же задачу,
переформулировав ее так: "В какие моменты
времени положение материальной точки
относительно начала координат составит s = 6 м?".
Иначе, требуется найти выражения и численные
значения корней квадратичного уравнения
относительно неизвестной t.
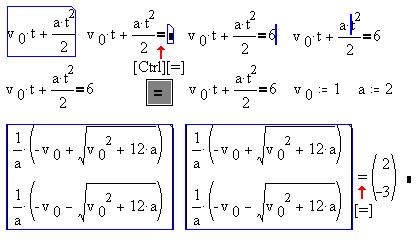
Опишем порядок действий: напечатав выражение
(формулу пути), выделили его синей рамкой и с
помощью кнопки панели символов или клавишами
[Ctrl][=] ввели знак логического равенства,
"не требующего" численных значений
переменных (у него "полужирное" начертание),
и правую часть нашего уравнения - 6. Затем
отметили маркером ввода переменную t (в любом
месте выражения) и в меню Символика
выбрали команду Решить относительно
переменной: ниже выражения появился столбец
формул корней уравнения. Теперь для получения
численных значений корней введем выше
(рядом с уравнением) значения для начальной
скорости и ускорения. После этого выделим
столбец формул для корней (щелчком по его
скобкам) и, нажав клавишу [=], получаем столбец
численных значений корней: на отметке 6 м
материальная точка побывала дважды: спустя две
секунды после начала отсчета времени
(разгоняясь) и за три секунды до начала отсчета
(при торможении).
Замечание. Если бы мы не ввели правой части
равенства, то по умолчанию она считалась бы
равной 0:
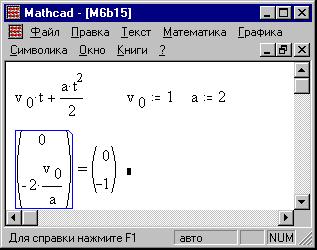
Для того, чтобы рассмотреть полностью движение
материальной точки в нашей задаче, нужно
определить путь как функцию дискретного
аргумента t: s(t). Для переменной t определим
нижний (0) и верхний (5) пределы изменения
аргумента, а также шаг изменения ,
прибавив после запятой этот шаг к нижнему
пределу (по умолчанию шаг равен 1):
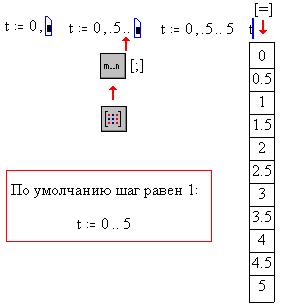
Как видим, после определения дискретного
аргумента знак [=] возвращает таблицу
(одномерный массив) его значений. Заметим,
что многоточие в определении переменной -
это не две подряд напечатанные точки [.], а специальный
символ(кнопка на панели символов либо клавиша
[;]). Заметим также, что "ноль целых" указывать
не обязательно: 0.5 = .5.
Точно так же определим функцию дискретного
аргумента:

При сравнении таблиц отмечено стрелкой одно
решение уравнения движения, уже найденное с
помощью символьной математики.
Задав конкретное значение переменной t,
получаем соответствующее значение функции s(t) с
помощью знака равенства [=]. Найдем, например,
положение материальной точки в момент времени 3 с
до начала отсчета:
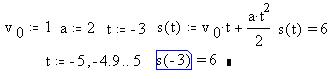
Во втором определении переменной t как
дискретного аргумента шаг его изменения равен 0.1:
-5 + 0.1 = -4.9.
Построим график зависимости s(t), вставив его с
помощью кнопки на панели символов либо клавишей
[@], либо командой Декартов график меню Графика
:
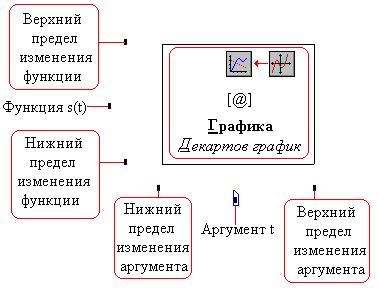
Напечатаем имя переменной t, затем,
"прыгая" с помощью клавиши [Tab] по черным
прямоугольникам либо щелкнув мышью по месту
ввода имени функции, напечатаем s(t). После этого
щелкнем мышью вне графика либо нажмем
клавишу [F9] (или [Enter]):
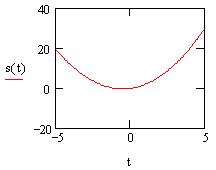
Щелкнув по графику, выделим его синей рамкой,
при этом рядом с пределами изменения аргумента и
функции появились места изменения пределов
пользователем :
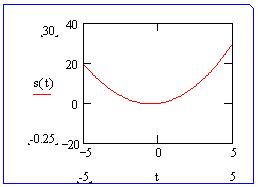
Давайте сузим область изменения аргумента
(увеличим масштаб графика) от -2 с до 2 с,
предварительно удалив -5 и 5, а затем впечатав -2 и 2:
Посмотрим на результат изменения масштаба:
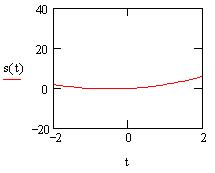
Увеличить какую-либо область графика можно
также с помощью инструмента "Лупа" в
меню Декартов график, заменяющего при
выделении графика меню Графика :
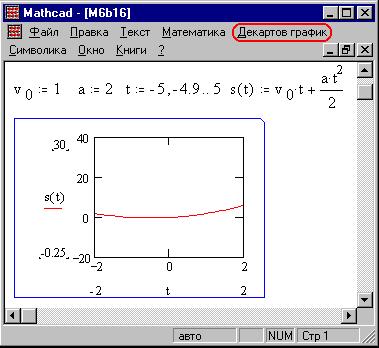
Выбрав этот инструмент, натянем на графике
пунктирный прямоугольник выделения области:
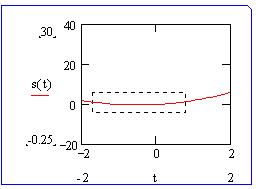
При этом в диалоговом окне фиксируются
XY-координаты углов выделенной области:
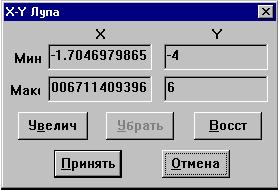
Щелкнем по кнопке Увелич и, чтобы
сохранить новый масштаб, по кнопке Принять :
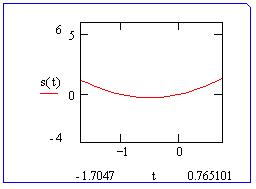
Чтобы восстановить исходный масштаб,
нужно в том же порядке вызвать диалоговое окно
инструмента "Лупа" и в нем щелкнуть по
кнопке Восст .
Главный инструмент форматирования (изменения)
графика - это команда Формат меню Декартов
график. Ее, впрочем, проще выбрать двойным
щелчком мыши по графику. Появляется диалоговое
окно:
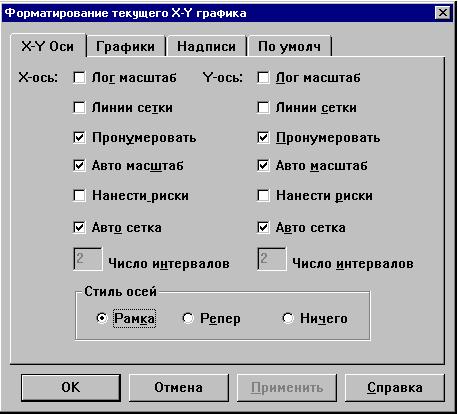
Сейчас установки окна - по умолчанию.
Закладка "X-Y оси":флажки Пронумеровать
проставляют числовые значения делений осей;
количество делений- интервалов можно
установить от 2 (по умолчанию) до 99 (выключив
флажки Авто сетка); вместо делений
можно провести линии сетки зеленого цвета;
предельные значения данных на осях не
превышают указанных пользователем, если
выключить флажки Авто масштаб. Флажки Нанести
риски позволяют провести две горизонтальных и
две вертикальных пунктирных линии красного
цвета, положение которых относительно осей можно
указать числом либо формулой. Флажок Репер
заменяет Рамку на координатные оси. Кнопка Применить
позволяет просмотреть результат форматирования,
не закрывая диалогового окна (закрывают
его кнопки ОК или Отмена ).
Отформатируем наш график следующим образом:
отключим по обеим осям Авто масштаб; включим
Линии сетки, выключив Авто сетка и
установив для обеих осей 3 деления; включим для
обеих осей Нанести риски,при этом введем для
одной риски по оси Х значение (-1), а для одной
риски по оси Y значение s(1); наконец, заменим Рамку
на Репер. Вид форматируемого графика с
черными прямоугольниками для двух невведенных
значений рисок:
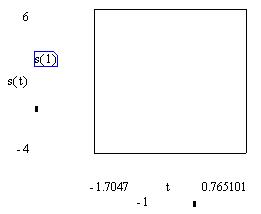
Итог форматирования:
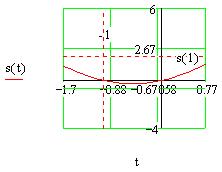
Натянув на график пунктирную рамку выделения,
увеличим его размер:
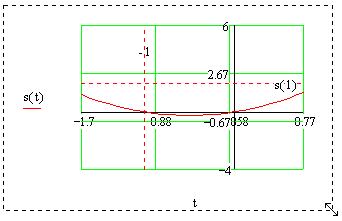
Откроем теперь закладку "Графики
", вызвав двойным щелчком мыши по графику
диалоговое окно формата:
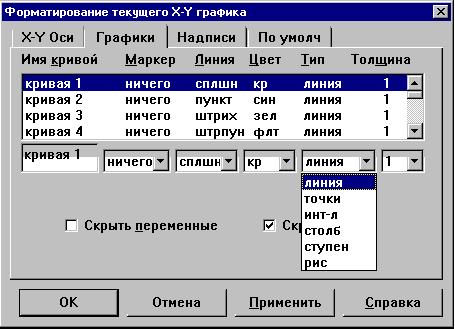
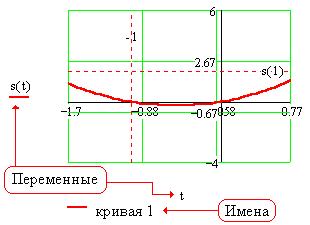
Установим для нашей кривой 1 другую Толщину,
равную 2 пиксела, выключим флажки Скрыть
переменные и Скрыть имена :
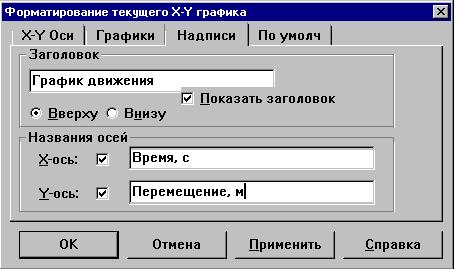
Откроем в окне формата закладку "Надписи
". Включим флажки показа заголовка и названий
осей и введем названия:
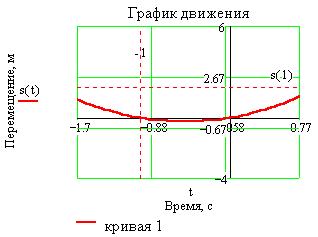
Теперь получаем окончательный вид графика:
Закладка "По умолчанию"
позволяет установить форматы закладок "X-Y
оси" и "Графики " по
умолчанию пользователем или, наоборот, изменить
установки пользователя на установки по
умолчанию.
Двойным щелчком мыши по каждой оси координат
можно вызвать диалоговое окно форматирования
осей (как, например, для оси Y) :
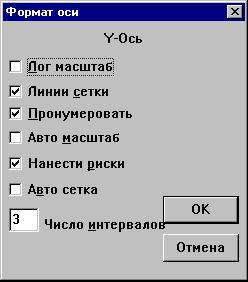
Весьма интересный, особенно в сочетании с
инструментом "Лупа", инструмент "Графики"
(своего рода визир) в меню Декартов график.
Выбрав его и удерживая нажатой мышь, переместим
ее указатель в форме пунктирного перекрестья
по графику. Координаты точек графика будут
отображены в диалоговом окне:
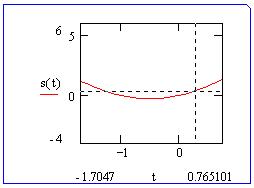 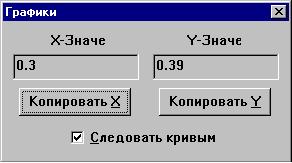
Заметим, что, выключив флажок Следовать
кривым , перекрестье визира можно перемещать
по любым точкам плоскости графика. Кнопки
копирования значений координат в буфер обмена
позволяют затем вставить эти значения в
математическое выражение или текст.
На одной оси ординат можно построить до 16
графиков функций одного аргумента или до 10
графиков функций разных аргументов. Разумеется, функции
и границы изменения аргументов должны быть
совместимых размерностей (а также, заметим,
сопоставимых размеров для повышения качества
наглядности).
Рассмотрим для примера сложное
кусочно-непрерывное движение материальной
точки.
Первый промежуток времени материальная точка
двигалась, замедляясь, как в нашей задаче.
Остановившись за 0,5 с до начала отсчета времени,
она до 1 с после начала отсчета времени покоилась.
Затем двигалась равномерно. Уравнения движения
(введенные просто как имена функций на графике) и
моменты интервалов времени движения (имена
переменных на графике) разделены запятыми:
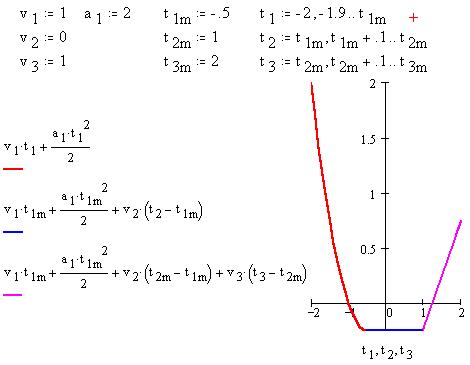
"Живой" график позволяет более наглядно
"стыковать" уравнения сложного движения.
Вернемся опять к первоначальной задаче.
Формула тангенса угла наклона касательной к
графику перемещения получается в результате дифференцирования
формулы перемещения по времени и имеет
физический смысл мгновенной скорости
материальной точки. Наоборот, формула
перемещения есть результат интегрирования формулы
мгновенной скорости:

Геометрический смысл отрезка перемещения -
это площаль трапеции под графиком мгновенной
скорости за тот же промежуток времени или
определенный интеграл от мгновенной скорости.
Определив мгновенную скорость как функцию
времени, найдем перемещение за промежуток от 0 с
до 1с как площадь под графиком мгновенной
скорости:
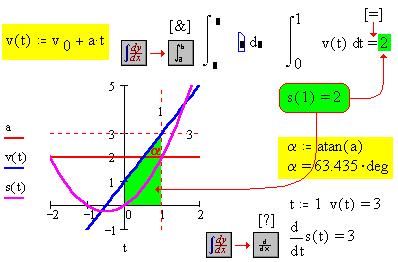
Тангенс угла наклона графика мгновенной
скорости к оси времени численно равен ускорению.
Угол, как видим, равен 63,435°. Кроме того, находим,
что на первой секунде после начала отсчета
мгновенная скорость была равной 3 м/с, в т. ч. и как
численное значение производной перемещения по
времени. Вот для сравнения соответствующий
документ MathCAD:
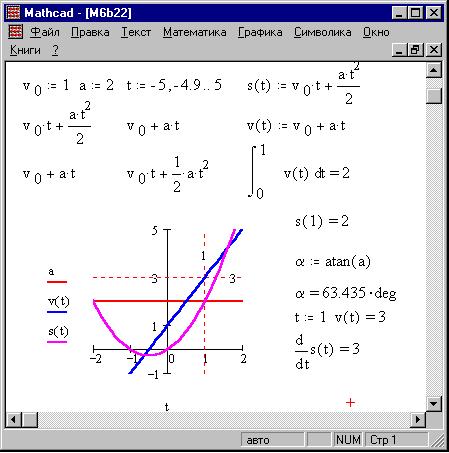
Заметим, что число интервалов по осям
установлено различным. Толщина линий графиков - 2
пиксела. Вставлены риски: по одной на каждую ось.
Автомасштаб по осям выключен.
Найдем среднюю скорость движения
материальной точки в интервале времени от 1 с до 5
с от момента начала отсчета времени - она равна
отношению пройденного пути к промежутку времени:
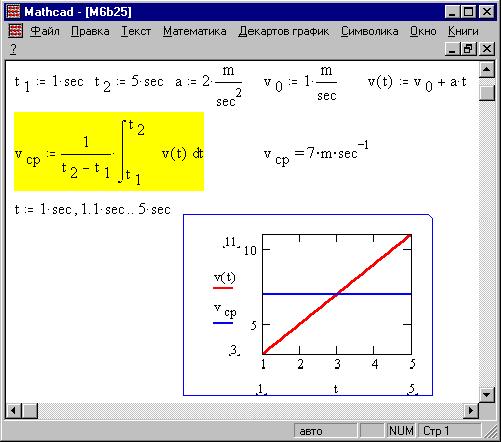
Очевидно, площади под графиками скорости и
средней скорости одинаковы.
Кстати, желтый фоновый прямоугольник для
формулы средней скорости "включается" (и
"выключается") командой Подсветить
выражение в меню Математика. А в меню Окно
соответствующими командами можно изменить
цвета фона ("бумаги"), формул, текста и
подсвеченных выражений :
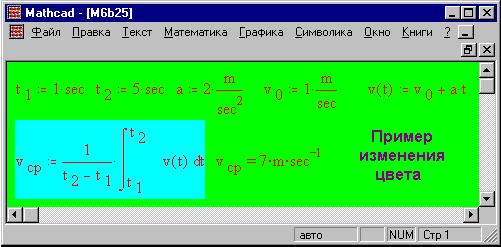
Вот типичный вид диалогового окна для
изменения цвета (например, фона):
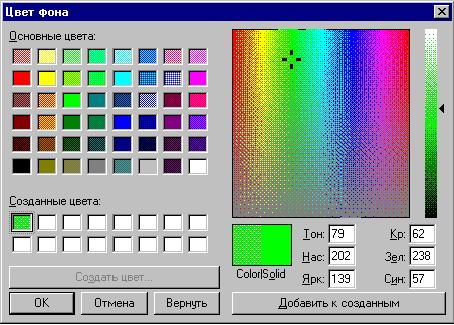
В окне мы, выбрав команду (кнопку) Создать
цвет..., щелкнули мышью по спектру оттенков
(черный крестик), уточнили оттенок, переместив
мышью черную стрелку справа от спектра вниз, и добавили
к созданным, а затем щелкнули по созданному
цвету . Теперь кнопка "ОК" выделена и
"готова" к изменению цвета фона на созданный
нами.
Уточним теперь понятие массива как упорядоченной
последовательности: у каждого элемента
массива есть свой порядковый номер
(целочисленный). Можно использовать этот номер
(пусть это будет дискретная целочисленная
переменная i) для задания произвольной
дискретной переменной, включив его в её
выражение:
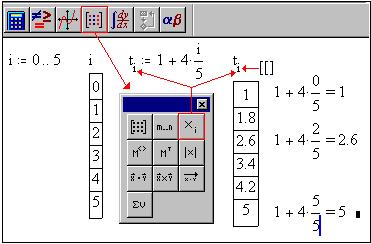
Как видим, здесь шаг изменения переменной t
равен 4*1/5 = 0,8. Чтобы уменьшить шаг, достаточно
увеличить конечное значение порядкового номера i
элементов массива ti. Например, при i =
0..10 шаг равен 4*1/10 = 0,4.
Такой способ задания дискретной переменной
необходим для создания графика поверхности
функции двух переменных:
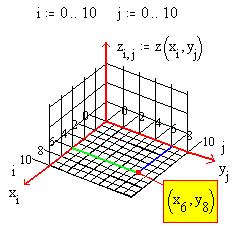
Как видим на рисунке, плоскость x0y разбивается
на i*j прямоугольных ячеек (в нашем примере i = 10 по
оси 0x и j = 10 по оси 0y). Для каждого значения i (j)
определяется, как на предыдущей странице,
значение дискретного аргумента xi (yj ). Далее, определяем функцию двух
аргументов, например, 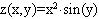 и для каждой ячейки определяем
значения z(xi,yj), которые и
отображаются на графике (команда График
поверхности из меню Графика либо
клавиши [Ctrl][2], либо кнопка и для каждой ячейки определяем
значения z(xi,yj), которые и
отображаются на графике (команда График
поверхности из меню Графика либо
клавиши [Ctrl][2], либо кнопка  на панели графиков): на панели графиков):
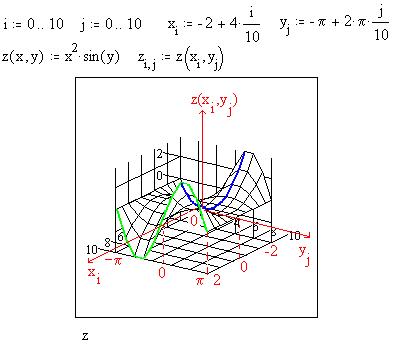
Высота (относительно плоскости x0y) узлов сетки,
образующей поверхностный график, равна z(xi,yj). Узлы соединяются отрезками прямых.
На рисунке выделено синим цветом сечение
поверхности вдоль оси 0x, соответствующее y=y7, и зеленым цветом сечение вдоль оси 0y,
соответствующее x=x10. Давайте получим
эти же сечения на декартовом графике, назвав их,
соответственно, zxi и xyj :
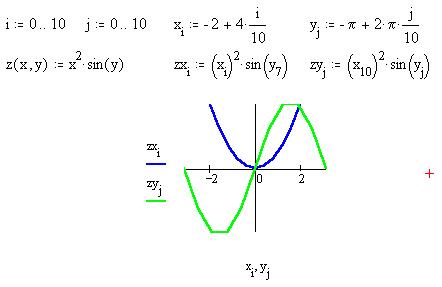
То, что на графике поверхности отображены
узловые значения, хорошо видно в форме 3-мерного
(3D: 3 dimensions - 3 измерения) графика - точечного
графика, выбираемой в диалоговом окне
форматирования (команда Формат 3D графика в
меню Графика либо двойной щелчок по
графику):
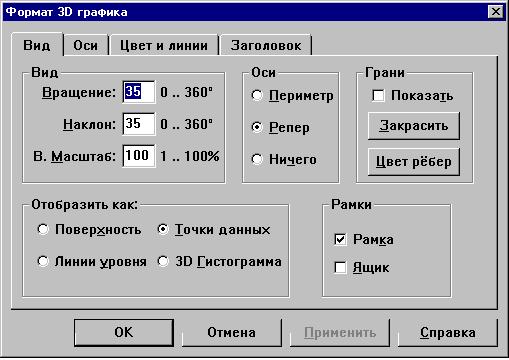
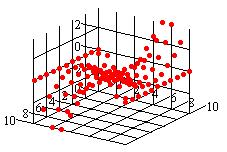
В закладке Вид окна формата 3-мерного
графика вернемся к графику поверхности и откроем
закладку Цвет и линии :
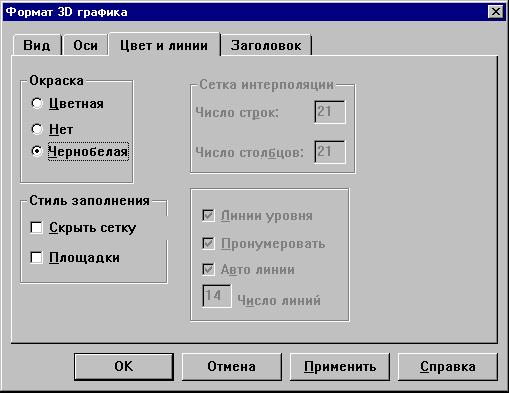
Выберем Окраска Чернобелая, затем Цветная,
при этом отключим флажок Скрыть сетку. После
этого, включив флажок Площадки, получим
промежуточную между поверхностью и
"столбчатой диаграммой" - 3D Гистограммой
- форму из площадок высотой, равной узловым
значениям. И, наконец, выберем форму 3-мерной
гистограммы:
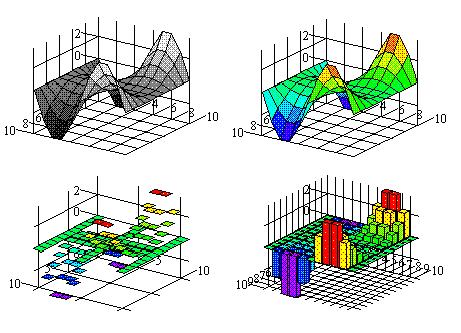
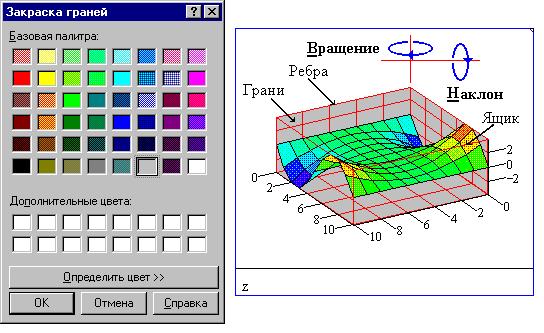
Вернемся к форме графика поверхности. Натянув
пунктирный прямоугольник выделения, растянем
график по горизонтали так же, как мы делали для
декартова графика. Покажем и закрасим
грани (в серый цвет) и ребра (в красный цвет);
установим Вращение и Наклон равными 60°,
а также включим флажок Ящик :
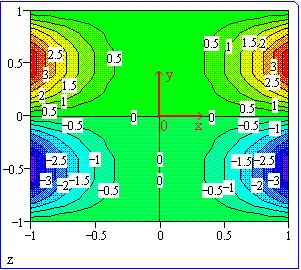
Если "посмотреть" на поверхность сверху,
установив наклон равным 90°, и заменить линии
сетки линиями уровня, соединяющими точки
равной высоты, то мы получим четвертую форму
представления функции двух переменный,
аналогичную географической карте (флажок Линии
уровня закладки Вид ):
Отключение изображения линий уровня, их
нумерации и количества производится
соответствующими флажками на закладке Цвет
и линии точно так же, как и отключение,
нумерация и количество линий сетки на
закладке Оси. Показ заголовка и
установление его позиции (внизу или вверху
графика) устанавливается на закладке Заголовок.
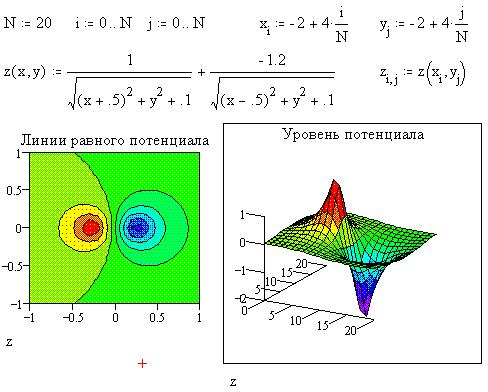
Для примера приведем графики линий уровня и
поверхности потенциала поля двух разноименных
точечных электрических зарядов:
Вернемся к предыдущей функции
"параболического синуса" и отобразим ее
график в форме Точек данных:
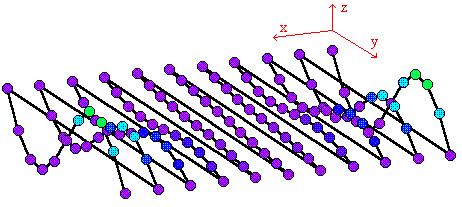
Для наглядности на закладке Вид
включен флажок Ничего для Осей,
выключен флажок Показать для Граней, а также
флажок Ящик (система координат красного
цвета нами дорисована).
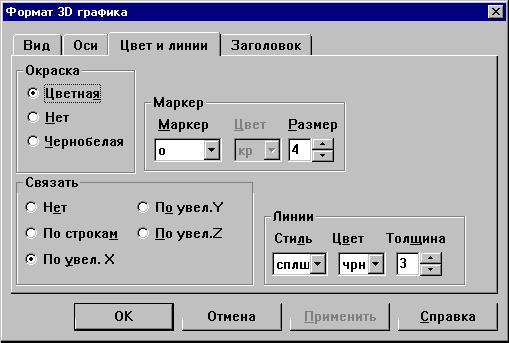
На закладке Цвет и линии выбраны:
размер маркера равным 4 пиксела, символ маркера
- о, толщина линии - 3 пиксела, цвет линии -
черный. Точки связаны по увеличению Х:
Следует отметить, что для получения точечного
пространственного графика не обязательно
задавать массив значений переменных: в этом
графике совокупность значений переменных -
суть координаты точки. Сами переменные могут
определяться всего одним целочисленным
параметром , который может иметь физический
смысл длины, времени и т. п. и поэтому иногда
называется "естественным параметром".
Построим несколько точек, лежащих на диагонали
параллелепипеда, связав их по увеличению Z
(команда Точечный график в меню Графика
):
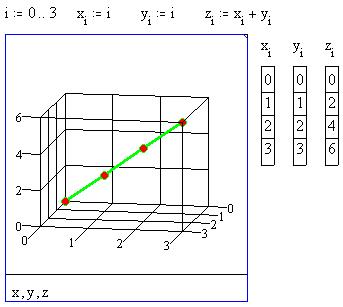
Если бы мы в качестве маркера выбрали Ничего
, то график представлял бы одну соединительную
линию - диагональ параллелепипеда.
Рассмотрим траекторию движения заряженной
частицы, влетающей под углом к силовым линиям
однородного магнитного поля, - известно, что эта
траектория представляет собой пространственную
спираль: в плоскости x0y частица движется
равномерно по окружности радиуса R и
одновременно совершает равномерное перемещение
вдоль оси z. Целочисленный параметр t отражает
время движения:
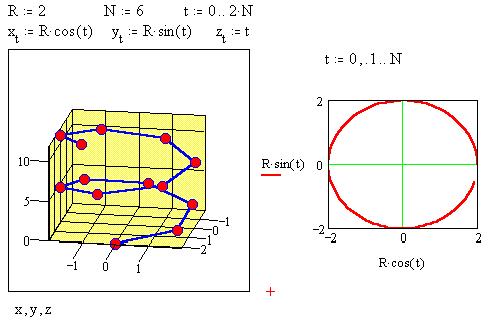
Рядом на декартовом графике отображена
проекция траектории на плоскость x0y: параметр t
уже не целочисленный, и шаг его изменения
дополнительно установлен равным 0,1.
Литература:
MATHCAD 6.0 PLUS. Финансовые, инженерные и
научные расчеты в среде Windows 95./Перевод с англ. - М.:
Информационно-издательский дом "Филинъ", 1996.
- 712 с.
Содержание
Вернуться на страницу
<Методические разработки> |

