Вернуться
на страницу <Методические разработки>
Содержание
Элементы линейной алгебры (правило Крамера)
Речь пойдёт о нахождении координат точки в
эвклидовом пространстве (в частном случае n x n
системы линейных уравнений A·x = b такой, что rang(A) =
rang(A|b) = n), доступном для понимания обычному
старшекласснику и применяемом для расчёта
электрических цепей, в т. ч. используя MathCAD.
Пример 1. Одномерное пространство -
прямая линия.
Вид уравнения, определяющего точку с
координатой 5 на оси x (см. рис. 1), очевиден:
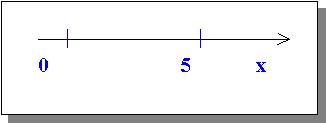
Рис. 1
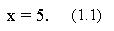
Ясно, что общий вид такого уравнения имеет
форму:
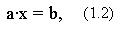
откуда находим решение:
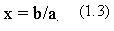
Пример 2. Двухмерное пространство -
плоскость.
Найдем координаты точки М
пересечения прямых, проведённых через точки
координатных осей x1, x2 как на рис. 2:
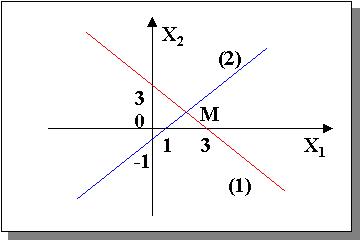
Рис. 2
Итак, как это видно из рис. 2 для прямой
(1), если x1 = 0, то x2 = 3 и если x2 = 0, то x1 = 3. Очевидно,
этим условиям удовлетворяет уравнение
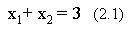
Для прямой (2) x2 = -1 если x1 = 0 и x1 = 1 если x2 =
0, чему удовлетворяет уровнение
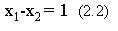
Найдём решение системы двух линейных уравнений
(2.1) и (2.2), т. е. координаты точки М,
принадлежавшей одновременно и прямой (1) и
прямой (2), методом подстановки:
- из (2.1) имеем: x1 = 3- x2;
- подставив это выражение в (2.2), получаем: x2 = 2;
- подставив это значение в (2.1), получим: x1 = 1.
Замечание. Можно сделать общий вывод,
что система двух линейных уравнений типа
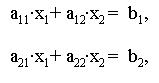
если она имеет единственное решение, имеет
геометрический смысл пересекающихся в одной
точке плоскости прямых, и это решение - суть
координаты точки пересечения прямых.
Здесь первый индекс коэффициентов при
неизвестных соответствует номеру уравнения,
второй - номеру неизвестной. Индекс свободных
членов соответствует номеру уравнения.
Пример 3. Трехмерное пространство.
Здесь точка есть место пересечения двух прямых,
а прямые - пересечением плоскостей. Аналогично
выглядит вершина пирамиды, образованная
пересечением двух рёбер - общего
геометрического места трёх граней (см. рис.
3).
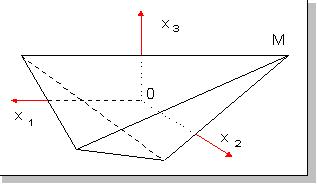
Рис. 3
Плоскость каждой грани задаётся линейным
уравнением относительно трёх неизвестных x1, x2 и
x1, - итого три линейных уравнения:
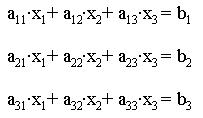
Ясно, что нахождение решений системы трех
уравнений, т. е. пространственных координат
вершины пирамиды, методом подстановки
становится довольно громоздким (не говоря уж о
большем числе переменных).
Более эффективные методы нахождения решений
систем линейных уравнений - предмет линейной
алгебры, особого раздела высшей математики.
Один из таких методов носит название правила
Крамера. Суть его можно выявить уже при
решении системы двух уравнений в общем виде.
Запишем систему из двух линейных уравнений в
общем виде:
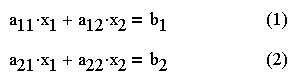
Здесь aij - коэффициент при j-й
неизвестной в i-м уравнении; - свободный член в i-м
уравнении.
Из первого уравнения найдем выражение для
неизвестной :
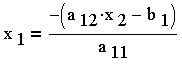
Подставим найденное вместо во втором
уравнении:
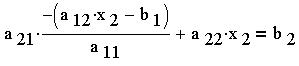
Откуда найдем выражение для переменной :
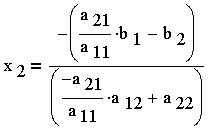
Или, после упрощения:
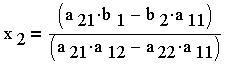
Подставим полученное выражение во второе
уравнение исходной системы:
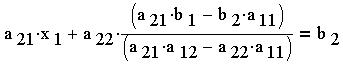
Откуда находим выражение для переменной :
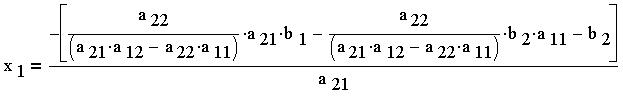
Или, после упрощения:
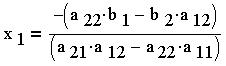
Наконец, в более удобной форме записи:
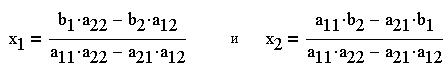
Для наглядности представим таблицу - матрицу
коэффициентов при неизвестных, а также матрицу - столбец
свободных членов системы уравнений:
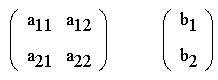
Сравнивая с формулами для неизвестных,
замечаем, что одинаковый знаменатель в обоих
выражениях есть алгебраическая сумма
произведений элементов разных строк и,
одновременно, разных столбцов матрицы
коэффициентов.
Числители представляют из себя
совершенно аналогичную сумму для матриц, в
которых столбец коэффициентов при
соответствующем неизвестном заменен на столбец
свободных членов:
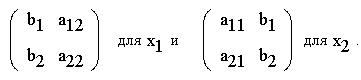
Очевидно, что произведение "слева - направо и
вниз" (назовем это направление "вдоль главной
диагонали матрицы") имеет знак "+", а
"слева - направо и вверх" (назовем это
направление "вдоль побочной диагонали
матрицы") имеет знак " - " (рис. 4):
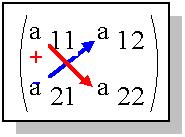
Рис. 4
Число, получающееся из такой суммы
произведений, назовем определителем
(детерминантом) матрицы. Нахождение решений
системы уравнений как отношений соответствующих
определителей носит название правил Крамера.
Положим, что определитель матрицы 1x1,
состоящей из единственного элемента-числа, равен
самому числу (обозначается определитель
прямыми скобками):
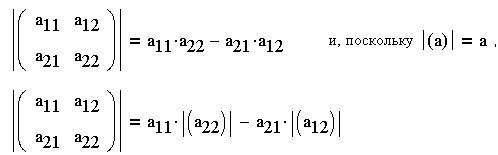
Матрица  получается из матрицы
получается из матрицы  после удаления (зачеркивания) строки и
столбца, на пересечении которых находится
элемент (рис. 5): после удаления (зачеркивания) строки и
столбца, на пересечении которых находится
элемент (рис. 5):
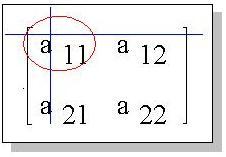
Рис. 5
Определитель такой "меньшей" матрицы
называется минором элемента 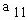 . Заметим также,
что знак перед произведением элемента на
его минор очевидным образом зависит от четности
суммы индексов (номеров строки и столбца)
элемента и может быть "уловлен" множителем . Заметим также,
что знак перед произведением элемента на
его минор очевидным образом зависит от четности
суммы индексов (номеров строки и столбца)
элемента и может быть "уловлен" множителем 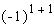 для первого
произведения и для первого
произведения и 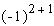 для второго произведения:
для второго произведения:
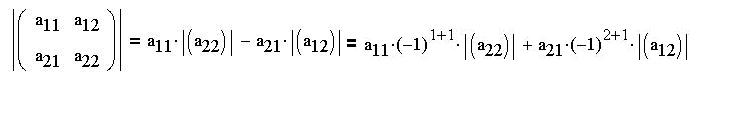
Произведение типа 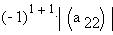 или "минор со знаком" называется алгебраическим
дополнением элемента или "минор со знаком" называется алгебраическим
дополнением элемента 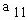 и обозначается и обозначается 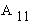
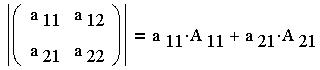
Мы получили формулу разложения определителя по
элементам первого столбца.
Покажем, что значение определителя можно найти
его разложением по элементам любого столбца или
любой строки (очевидно, критерием выбора будет
количество в них нулей !). Для этого будем
переписывать выражение 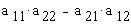 , "примеряя" прямые скобки миноров
всякий раз на другие элементы: , "примеряя" прямые скобки миноров
всякий раз на другие элементы:
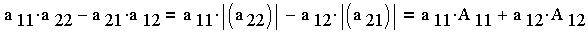
Это - разложение определителя по элементам первой
cтоки. Далее:
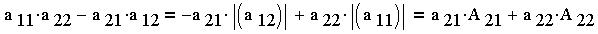
Это - разложение определителя по элементам второй
cтоки. Наконец:
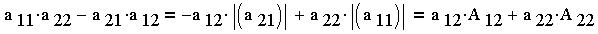
Это - разложение определителя по элементам второго
столбца.
Нахождение определителя матрицы методом
его разложения по элементам каких-либо строки
или столбца - общее правило, позволяющее (при
расчетах "вручную") шаг за шагом
уменьшать размер определителей.Убедимся в
этом на примере определителя матрицы 3x3 в общем
виде:
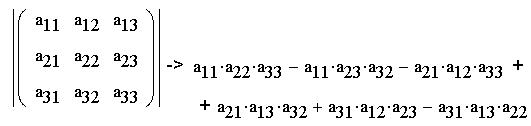
Перепишем этот результат, вынося за скобки
элементы, например, первой строки и обозначив
определитель (детерминант) греческой буквой
(дельта):
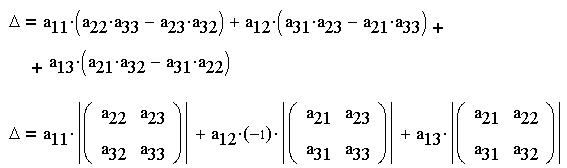
Здесь минор в алгебраическом дополнении,
например, элемента 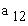 образован при удалении из исходной
матрицы первой строки и второго столбца, так как
они пересекаются как раз на элементе образован при удалении из исходной
матрицы первой строки и второго столбца, так как
они пересекаются как раз на элементе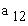 (рис. 6): (рис. 6):
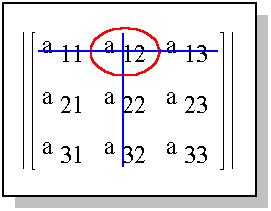
Рис. 6
Применив к нему "правило диагоналей",
получим выражение, противоположное по знаку
выражению в скобках при элементе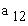 , отсюда (-1) перед этим минором.
Очевидно, что и здесь знаки учитываются
множителями типа , отсюда (-1) перед этим минором.
Очевидно, что и здесь знаки учитываются
множителями типа 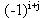 : :
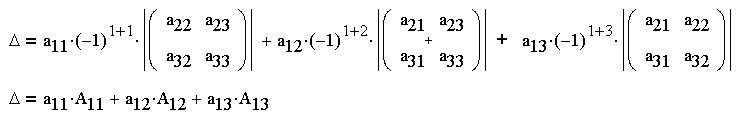
Мнемоническое правило "главной и побочной
диагонали" легко применить и для нахождения
определителя матрицы 3x3 (рис. 7), однако уже
при 4x4 элементов правило не эффективно.
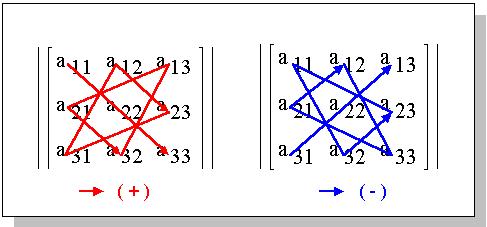
Рис. 7
Пример 4. Найдем определитель
матрицы 3x3:
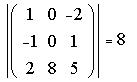
В самом деле, запишем, используя "правило
диагоналей":
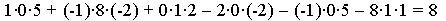
Найдем величину определителя методом его
разложения по элементам второго столбца (в нем
больше всего нулей!):
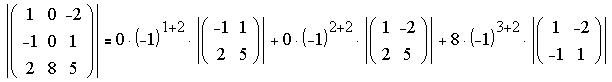
Первые два произведения заведомо нулевые,
третье же найдем, используя "правило
диагоналей":
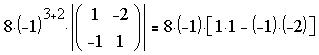
Последнее выражение равно .
Пример 5. Найдем решение системы из 4
линейных уравнений:
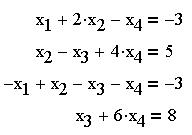
Перепишем для наглядности (впредь в этом шаге
не будет особой необходимости) систему уравнений
в так называемой "стандартной форме",
указывая, во-первых, и единичные коэффициенты и,
во-вторых, при отсутствии в уравнении какой-то
неизвестной, записывая ее с коэффициентом ноль:
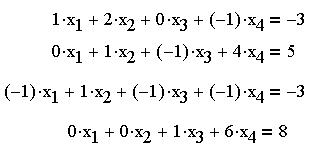
Обозначим буквой латинской буквой матрицу
коэффициентов при неизвестных и буквой столбец
свободных членов:
В символьной форме на языке матричной алгебры
система линейных уравнений записывается просто
в виде:
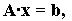
откуда вектор неизвестных - решение системы -
равен:
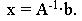
Можно также найти решения системы линейных
уравнений с помощью специальной функции Mathcad PLUS
lsolve(A,b), определив предварительно матрицу
коэффициентов при неизвестных А и вектор-столбец
свободных членов b.
Итак, для приведённой выше системы из 4-х
линейных уравнений MathCAD сразу же дает ответ:
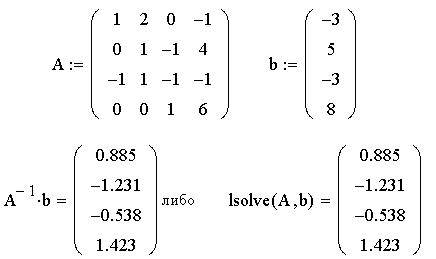
Мы же будем находить решения по правилу Крамера
как отношения определителей. Поэтому найдем для
последующей сверки значения всех нужных
определителей при помощи MathCAD, последовательно
заменяя в матрице А столбцы коэффициентов при
неизвестных на столбцы свободных членов b, и
получая матрицы А1,..,А4, определители которых,
согласно правилу Крамера, есть числители для
определения x1,..,x4:
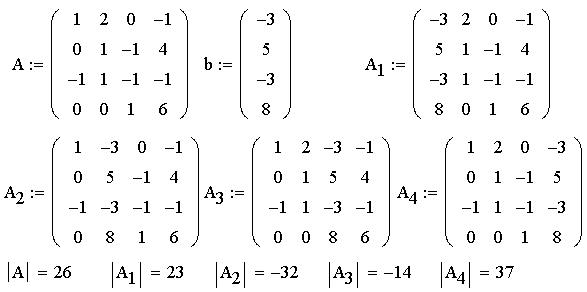
Найдем последнее решение "вручную". Для
расчета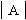 разложим
его по элементам первого столбца, а
определители-миноры найдем с помощью "правила
диагоналей". Определитель разложим
его по элементам первого столбца, а
определители-миноры найдем с помощью "правила
диагоналей". Определитель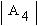 найдем разложением по элементам
четвертой строки. найдем разложением по элементам
четвертой строки.
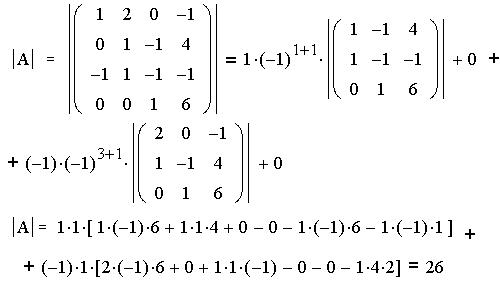
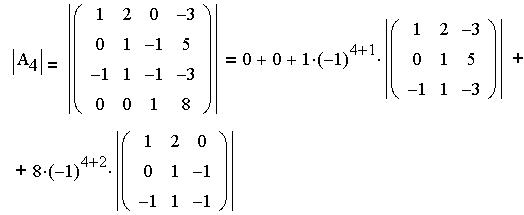
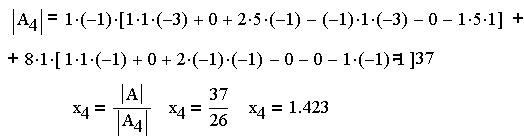
Пример 6. Расчёт электрической цепи
постоянного тока с помощью правил Кирхгофа.
Найдем токи в ветвях электрической цепи
постоянного тока с известными значениями
сопротивлений резисторов и ЭДС (пусть, например,
их численные значения равны их номеру в списке
элементов: R2 = 2 Ом, е1 = 1 В и т. д.) согласно схеме на рис.
8, используя правила Кирхгофа.
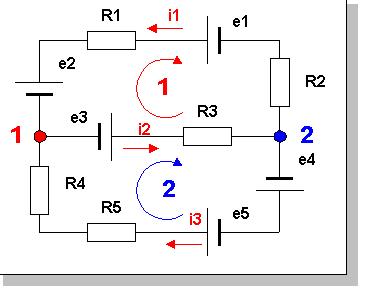
Рис. 8
Напомним, что последние - суть применение закона
сохранения электрического заряда и закона
сохранения энергии в форме равенства нулю
алгебраической суммы токов в N-1 из N узлов и
совпадения алгебраической суммы напряжений на
резисторах и алгебраической суммы ЭДС при обходе
всех "независимых" контуров(т. е.
включающих "новые" ветви). Направления токов
- произвольны (в случае неправильно угаданного
направления решение получится отрицательным, и
останется лишь поменять направление стрелки
тока на противоположное), направление обхода
одно и то же для всех контуров (например, как у нас
- по часовой стрелке). Например, как на рис. 8.
Конкретно, для узла 1 (красный цвет) запишем:
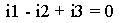
Для контура 1 (красный цвет):
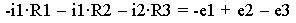
Для контура 2 (синий цвет):
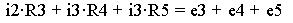
С учетом численных значений запишем в
стандартной форме:
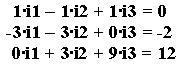
Выпишем матрицу коэффициентов при неизвестных
и вектор-столбец свободных членов системы
уравнений и применим функцию "lsolve",
содержащуюся в Mathcad PLUS:
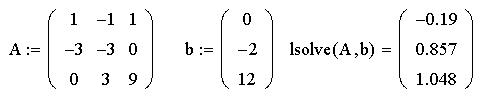
На схеме (рис. 8), по правилам Кирхгофа,
направление тока i1 нужно сменить на
противоположное.
Решения системы уравнений, т. е. численные
значения токов, соответственно, равны:
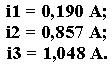
Умение находить решения систем линейных
уравнений позволяет учащимся более конкретно
исследовать электрические цепи различных
конфигураций, улучшая качество знаний в
нескольких рахделах курса физики, а также
оказывает существенную поддержку в последующем
образовательном процессе.
Содержание
Вернуться на страницу
<Методические разработки> |

