Вернуться
на страницу <Методические разработки>
Содержание
Элементы электротехники
2. МОДЕЛИРОВАНИЕ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
ПЕРЕМЕННОГО СИНУСОИДАЛЬНОГО ТОКА
Настоящее пособие отражает опыт работы
сотрудников МГДТДиЮ, МИРЭА, школ и межшкольных
учебных комбинатов по внедрению средств НИТ в
непрерывный образовательный процесс. Оно
ориентировано как на систему дополнительного
образования (учебно-творческие коллективы в
сфере НИТ, радиотехники, электроники и
электротехники), так и на систему общего
образования (компьютерная поддержка практикумов
по физике, математике, информационным
технологиям). Материалы пособия могут быть
использованы для дистанционного образования, в
т. ч. учащихся-инвалидов.
Учебный процесс на автоматизированном рабочем
месте (АРМ) учащихся, включающем ПЭВМ и
позволяющем использовать MathCAD и Electronics Workbench
ставит качественно новую задачу использования
элементов классической высшей математики при
изучении соответствующих разделов физики и
профориентационных дисциплин, углубляя знания
основных законов физики и, кроме того, оказывая
существенную поддержку в последующем
образовательном процессе (вуз, техникум).
Предлагаемое учебное пособие по виртуальному
(Electronics Workbench 5.12) и математическому (MathCAD 6.0 PLUS)
моделированию и расчету электрических цепей
представляет собой конспективное изложение
основных моментов теоретического и
экспериментального освоения некоторых разделов
электротехники на базе АРМ учащихся.
Особенностью содержания пособия является
использование комплексных чисел и метода
контурных токов для математического
моделирования и бескомпьютерного расчета
сложных разветвленных активно-реактивных цепей
переменного синусоидального тока, в т. ч.
трехфазных цепей с аварийными режимами работы.
Электронная версия пособия готовится к
размещению на WWW-серверах МГДТДиЮ и МИРЭА в
разделе "Программно-методические фонды в
сфере НИТ".
Создадим в Electronics Workbench 5.12 виртуальную
электронную модель разветвленной электрической
цепи переменного синусоидального тока:
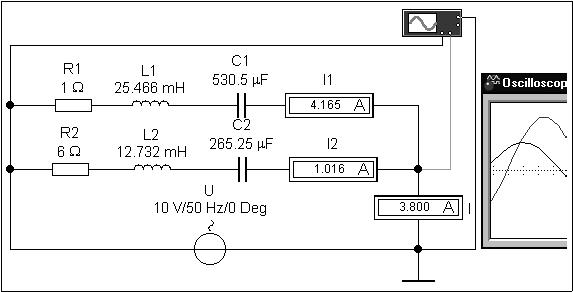
Нагрузка в первой ветви имеет
активно-индуктивный, а во второй -
активно-ёмкостный характер. В целом цепь
активно-индуктивная: осциллограмма напряжения,
прямо пропорционального силе суммарного тока,
снимаемая (на канал B осциллографа) с активного
внутреннего сопротивления амперметра I, равного 1
мОм, отстает от осциллограммы напряжения
источника питания (канал A).
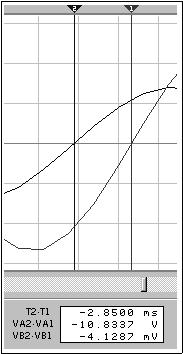
Определим по временным диаграммам
запаздывание синусоиды тока относительно
синусоиды напряжения:
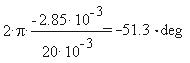
Создадим в MathCAD 6.0 PLUS математическую модель
цепи. Определим русские имена размерностей в СИ
через встроенные:
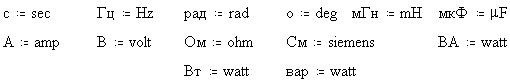
Определим частоту, угловую частоту, период и
действующее значение для источника
синусоидального напряжения; для построения
графиков определим также время как дискретный
аргумент:

Определим параметры элементов первой ветви как
в виртуальной модели. Определим и найдем
величины активного, реактивных и полного
сопротивления ветви, а также угол j 1IU сдвига фаз
тока I1 относительно напряжения U:
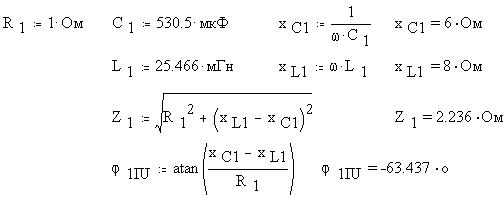
Проведем те же действия для второй ветви:
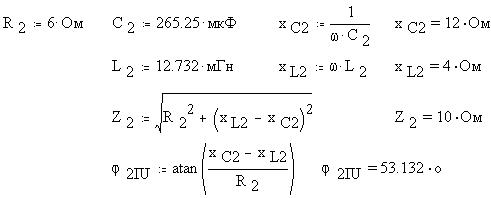
По закону Ома определим действующие значения
токов в ветвях. Определим функцию мгновенного
значения напряжения и, также согласно закону Ома,
определим функции мгновенных значений токов.
Найдем действующие значения токов и как средние
квадратичные за период их мгновенных значений:
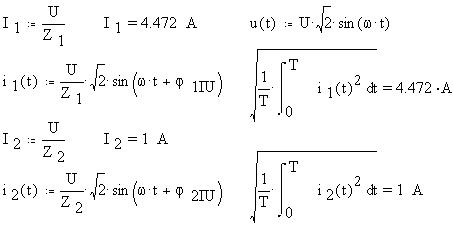
Определим функцию мгновенного значения
суммарного тока и найдем, как и выше, его
действующее значение:
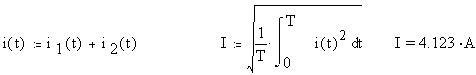
Задав начальное значение угла сдвига фаз
полного тока относительно напряжения равным 0
рад, найдем этот неизвестный угол как численное
решение уравнения в нулевой момент времени:
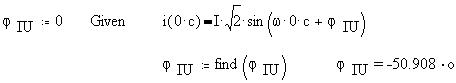
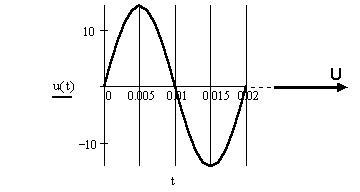
Построим на декартовом графике временную
диаграмму напряжения и создадим по ней в Visio Express
Drawing 3.0 векторную диаграмму:
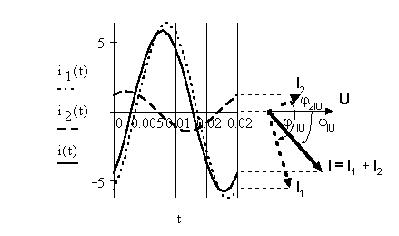
Точно так же создадим временные и векторную
диаграммы токов:
Найдем относительную погрешность результата в
виртуальной модели относительно математической,
например - для угла сдвига фазы между полным
током и напряжением:
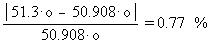
Рассчитаем значения токов в ветвях, используя
понятие проводимости, величины, обратной
сопротивлению.
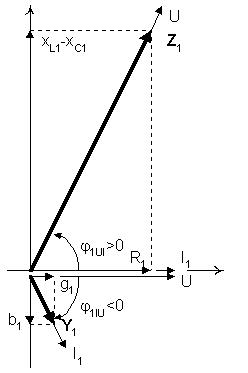
Вектор полной проводимости первой ветви Y1 коллинеарен вектору силы тока I1 и в системе координат относительно
вектора напряжения U, общего для обеих ветвей,
образует с ним угол  1IU, равный по абсолютной величине и
обратный по знаку углу
1IU, равный по абсолютной величине и
обратный по знаку углу  1UI напряжения
относительно тока, как на рисунке. 1UI напряжения
относительно тока, как на рисунке.
Модуль вектора проводимости равен величине,
обратной модулю вектора полного сопротивления Z1. Горизонтальная составляющая  1 вектора
Y1 называется "активной
проводимостью", а вертикальная составляющая b1 - "реактивной". 1 вектора
Y1 называется "активной
проводимостью", а вертикальная составляющая b1 - "реактивной".
Определим формулы расчета проводимостей 1-й
ветви по диаграмме проводимостей, найдя значения
тригонометрических функций угла из диаграммы
сопротивлений:
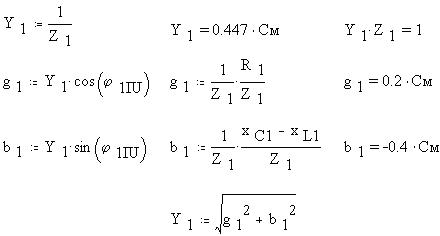
Аналогично определим проводимости второй
ветви и по векторной диаграмме проводимостей
найдем полную проводимость цепи и угол сдвига
фаз полного тока цепи относительно напряжения.
Найдем также действующие значения токов ветвей и
полного тока.
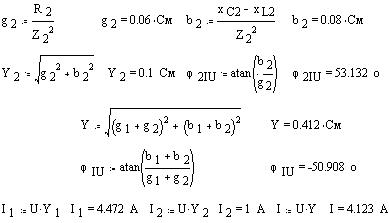
Сопротивление, согласно закону Ома, численно
равно работе по переносу +1 Кл электричества или
напряжению на участке цепи при силе тока, равной 1
А. Точно так же, проводимость численно равна силе
тока на участке цепи под напряжением 1 В. В этом
смысле такие процессы (работа по переносу заряда
и скорость переноса) естественно представимы на
временных и векторной диаграммах.
Зная действующие значения сопротивления и
проводимости 1-й ветви, а также определив
начальную фазу для синусоиды сопротивления
(вектор сопротивления коллинеарен вектору
напряжения), определим функции мгновенных
значений и по их графикам построим векторную
диаграмму:
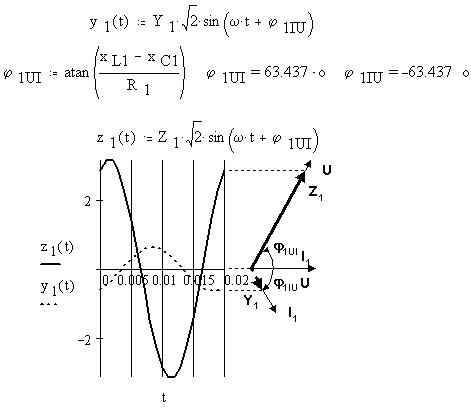
Приведем также "диаграммы отражений" для
синусоиды полного сопротивления 1-й ветви:
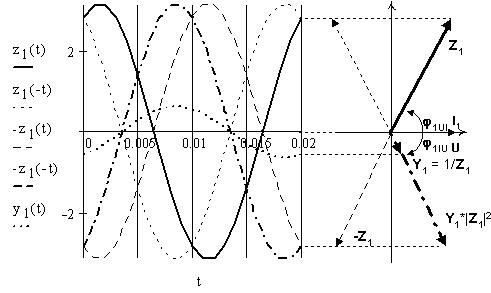
Оказывается, возможна форма математического
представления вектора в виде линейной
комбинации его горизонтальной и вертикальной
составляющих - их суммы, причем вертикальная
составляющая умножается на коэффициент, модуль
которого равен 1, на так называемую "мнимую
единицу" i (иногда j):
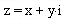
Такое представление вектора называется
"комплексным числом", при этом
горизонтальная составляющая именуется
"действительной частью", а вертикальная -
"мнимой частью" комплексного числа. В Mathcad
встроенные функции, возвращающие значения этих
частей, носят имена, соответственно, Re(z) (от real,
действительный) и Im(z) (от imaginary, мнимый), причем i
вводится сразу за числом, либо за 1, на которую
умножается выражение мнимой части.
Правила нахождения модуля комплексного числа и
обратного ему аналогичны нахождению модуля
полного сопротивления или проводимости
(импеданса и адмиттанса) цепи и переходу от
сопротивления к проводимости, а из условия, что
произведение комплексного числа на ему обратное
равно 1 следует, что 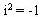 или что или что 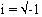 . Сложение и вычитание комплексных чисел
сводятся, как это естественно для представляемых
ими векторов, к сложению и вычитанию их
действительных и мнимых частей.
. Сложение и вычитание комплексных чисел
сводятся, как это естественно для представляемых
ими векторов, к сложению и вычитанию их
действительных и мнимых частей.
Покажем свойства комплексного числа на примере
численного значения полного сопротивления 1-й
ветви:
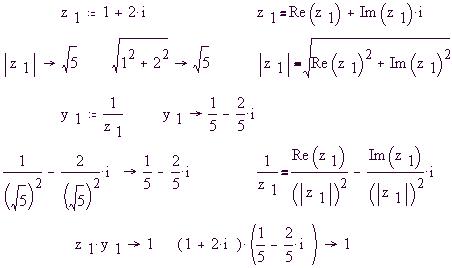
Перемножим выражения в скобках и убедимся в
необходимости того, что квадрат "мнимой
единицы" i равен по определению -1:
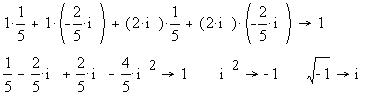
Проведем расчет рассмотренной выше цепи,
используя комплексное представление векторов,
представляющих в свою очередь гармонически
изменяющиеся во времени физические процессы, с
учетом размерностей величин:
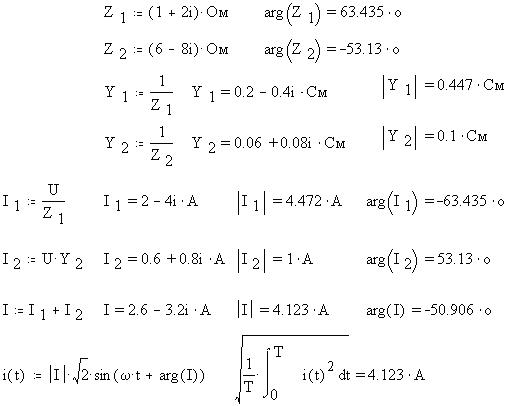
Рассчитаем полную проводимость всей цепи как
сумму проводимостей ветвей, определим активную и
реактивную проводимости и проведем расчет
полной, активной и реактивной мощностей, а также
"косинуса  "
нашей схемы: "
нашей схемы:

Активная и реактивная мощности всей цепи, как
компоненты вектора S, равны сумме одноименных
комплексных мощностей ветвей.
Применим правила Кирхгофа для расчета схемы.
Для системы уравнений получим в Mathcad cначала
численное и символьное решения, затем
воспользуемся встроенной функцией LSOLVE(A,b) для
нахождения корней системы линейных уравнений с
матрицей A коэффициентов при неизвестных и
вектором-столбцом b свободных членов. Наконец,
найдем "вручную" значение определителя |A|
матрицы комплексных коэффициентов при
неизвестных, имея в виду использование правил
Крамера при безкомпьютерном расчете цепи.
Определим комплексные векторы напряжения и
полных сопротивлений ветвей цепи. Для численного
решения системы уравнений зададим начальные
приближения решений - токов I1, I2 в ветвях и суммарного тока I источника
напряжения как мнимые единицы i:
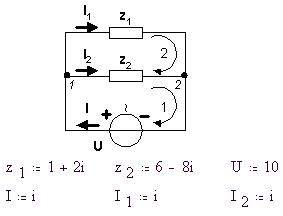
Для узла 1 запишем уравнение непрерывности
токов, а для контуров 1 и 2 приравняем сумму
падений напряжений сумме ЭДС при обходе контуров
по часовой стрелке, как на рисунке. Определим
также вектор-столбец решений:
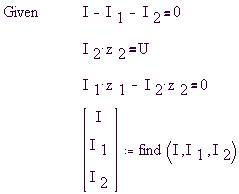
Найдем вектор-столбец модулей токов и
вектор-столбец их начальных фаз:
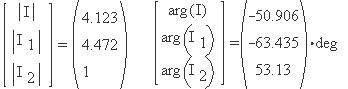
При символьном нахождении численных значений
неизвестных токов их начальные приближения
задавать не нужно, - достаточно задать, как и выше,
значения напряжения и сопротивлений ветвей, а
затем, определив вектор-столбец решений,
воспользоваться символьным знаком равенства (
[Ctrl] + [.] ):
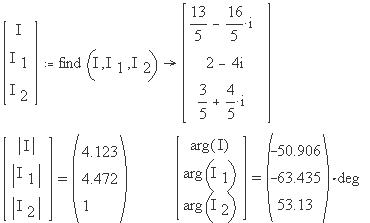
Наконец, зададим матрицу А коэффициентов при
неизвестных токах системы уравнений и
вектор-столбец b свободных членов:
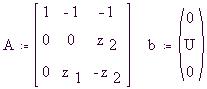
Найдем решение с помощью встроенной функции
LSOLVE(A,b):
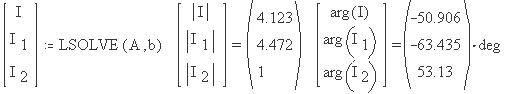
Найдя предварительно в Mathcad численное значение
определителя |A| матрицы A, рассчитаем его
значение сначала методом разложения по
элементам первого столбца, затем используя для
расчета определителя 2-го порядка мнемоническое
"правило диагоналей":
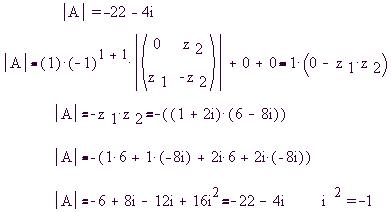
Уменьшить число уравнений в решаемой системе
на количество, равное числу уравнений по 1-му
правилу Кирхгофа, позволяет ввод условных
круговых контурных токов (все - по или
против часовой стрелки), значение которых на
"периферийных" ветвях совпадает со
значениями токов ветвей, а токи "внутренних"
ветвей цепи равны разности смежных контурных
токов:
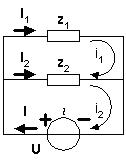
Контурный ток i1 совпадает с током I1 первой ветви, контурный ток i2
совпадает с током источника напряжения I. Ток
второй ветви I2 равен разности
контурных токов i2, совпадающего по
направлению с током I2 (в
соответствии с направлением ЭДС внутри
источника и напряжения вне его), и i1,
что не противоречит уравнению непрерывности
токов и закону сохранения электрического заряда
для узлов цепи (1-му правилу Кирхгофа):
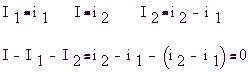
Обходя контуры по направлению контурных токов,
в нашем случае - по часовой стрелке, записываем 2-е
правило Кирхгофа.
На сопротивлении z1 при обходе по
часовой стрелке 1-го контура напряжение
создается током i1 и равно
произведению i1z1; на
сопротивлении z2 напряжение
создается алгебраической суммой контурных токов
i1 и i2 (с учетом того, что
направление обхода сопротивления
противоположно току i2) и равно (i1 - i2)z2 .
Источники напряжения в 1-м контуре отсутствуют.
При обходе 2-го контура вдоль контурного тока i2 напряжение на сопротивлении z2
равно (i2 - i1)z2,
т. к. теперь направление тока i1
противоположно направлению обхода, и равняется
сумме ЭДС в контуре, а именно - напряжению U
источника.
Для двух контуров получили систему двух
линейных уравнений относительно двух
неизвестных контурных токов:
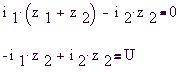
Определим матрицу A коэффициентов при
неизвестных и вектор-столбец b свободных членов,
затем применим встроенную функцию LSOLVE(A,b):
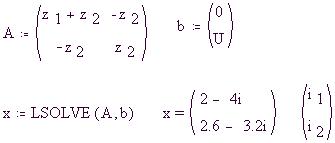
С учетом того, что в Mathcad номер первых строки и
столбца по умолчанию равен 0, определим токи в
ветвях:
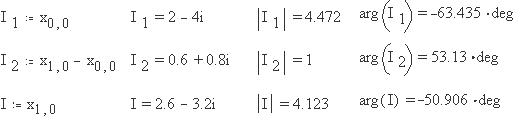
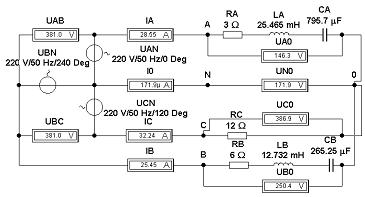
Воспользуемся методом контурных токов для
расчета токов и напряжений в трехфазной цепи при
аварийном обрыве нулевого провода, как на
виртуальной модели в Electronics Workbench 5.12 ниже:
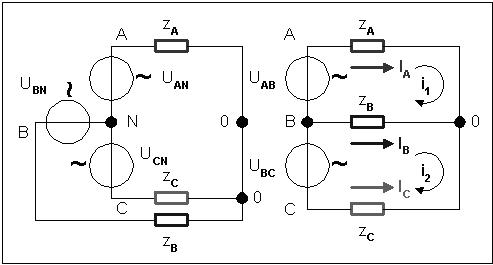
На рисунке ниже показана условная схема цепи с
обрывом нулевого провода и её эквивалентная
схема: фазные нагрузки оказались включенными под
линейные напряжения UAB и UBC.
Определим численные значения сопротивлений
фаз, линейных напряжений и составим систему из
двух уравнений относительно неизвестных
контурных токов i1 и i2
(как видно на схеме виртуальной модели, нулевая
начальная фаза определена для фазного
напряжения UAN трехфазного источника
напряжения, относительно которого начальные
фазы линейных напряжений UAB и UBC составляют, соответственно, +30° и -90°):

Определим матрицу A коэффициентов при
неизвестных, вектор-столбец b свободных членов
уравнений, а также вектор-столбец решений,
который найдем с помощью встроенной функции
LSOLVE(A,b):
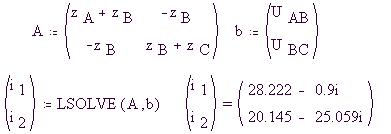
Определим фазные токи IA, IB
и IC через контурные i1 и i2 и найдем их:

Согласно закону Ома определим и найдем фазные
напряжения; сравнивая также рассчитанное
напряжение UC0 с показанием
соответствующего прибора на виртуальной модели,
определим относительную погрешность этого
показания относительно рассчитанного:
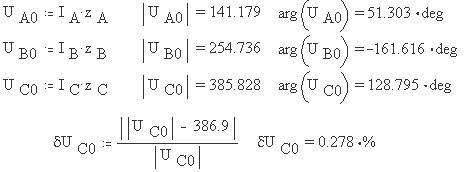
Определим теперь напряжение "смещения нуля
относительно нейтрали" N генератора U0N.
Для этого определим напряжение фазной обмотки
генератора UAN, затем найдем величину,
численно равную работе по переносу +1 Кл от 0 до N
по одному из возможных "маршрутов",
например: 0 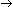 A A 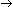 N, т. е. напряжение U0N как сумму напряжений U0A = -
UA0 и UAN: N, т. е. напряжение U0N как сумму напряжений U0A = -
UA0 и UAN:
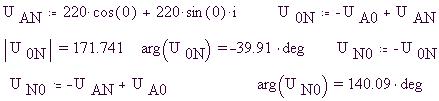
Определим функции мгновенных значений
линейного напряжения uAB(t), фазного uA0(t) и напряжений u0N(t) и u0N(t), затем создадим график, по которому
построим векторную диаграмму:
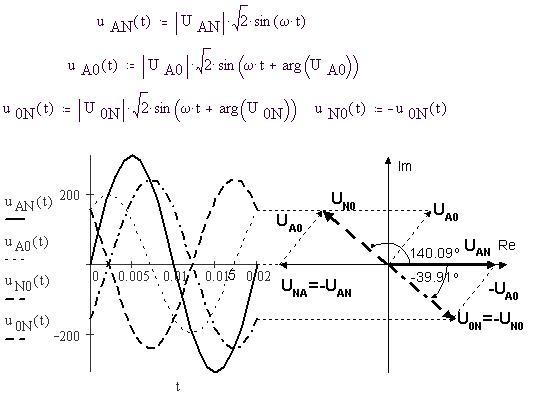
Получим осциллограммы напряжений uAN(t)
и u0N(t) на виртуальной модели. Для
этого условный нулевой уровень отсчета
("землю") присоединим к нейтрали, к ней же
присоединим клемму заземления осциллографа. На
канал А осциллографа подадим потенциал точки А
схемы, на канал В - точки 0:
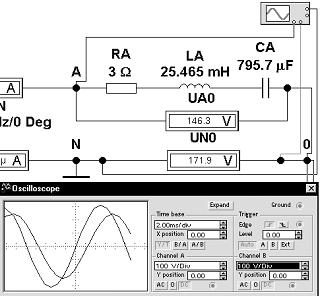
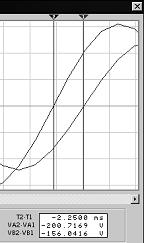
По временным диаграммам определим сдвиг фаз
между u0N(t) и uAN(t).
Временной сдвиг составляет, как это видно на
рисунке слева, -2.25 мс, что соответствует фазовому
сдвигу:
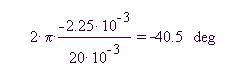
Найдем в Mathcad этот же сдвиг фаз как разность
аргументов соответствующих векторов:
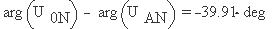
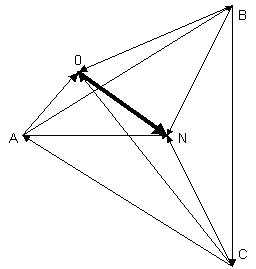
Представим фазные и линейные напряжения
генератора, фазные напряжения нагрузок и
напряжение смещения нуля на единой векторной
диаграмме:
Рассмотренную цепь также можно рассчитать,
начав с записи уравнения непрерывности токов (1-е
правило Кирхгофа) для узла 0 (см. эквивалентную
схему цепи на стр. 16, а также векторную диаграмму
напряжений выше):
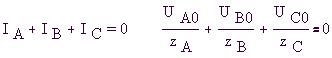
Выбрав в качестве единственной неизвестной
напряжение, например, UB0 при заданных
как выше сопротивлениях ветвей и линейных
напряжениях, получаем уравнение с одной
неизвестной, численное решение которого находим
в Mathcad:
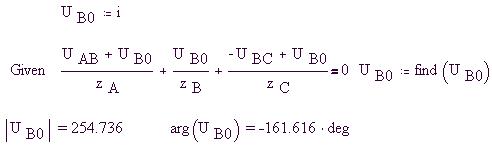
Теперь дополнительно определяем и находим токи
ветвей:
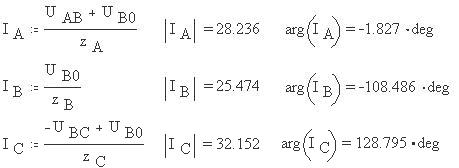
Литература:
- Касаткин А.С., Немцов М. В.
Электротехника: Учеб. пособие для вузов. - 4-е изд.,
перераб. - М.: Энергоатомиздат, 1983. - 440 с., ил.
- Edminister, Josef. Schaum's Outline of Theory and Problems of Electric
Circuits. Second Edition./McGraw-Hill, Inc., 1995.
- Ходяков И.А. Основы электротехники.
Часть I. Под ред. И.П. Дешко. Учебное пособие
/МГДТДиЮ, МИРЭА - М., 1998, 38с.
- Сборник творческих проектов учащихся 1998/99 уч.
года. Под ред. И.А. Ходякова/ МГДТДиЮ, МИРЭА - М., 1999,
50с.
Содержание
Вернуться на страницу
<Методические разработки> |

