Вернуться
на страницу <Методические разработки>
Содержание
Элементы электродинамики
Физический вакуум.
Свойства "пустого" пространства (вдали от
взаимодействующих тел) - физического вакуума
- предполагаются простейшими:
- пространство однородно, т. е. свойства
пространства не зависят от координат; другими
словами - свойства не меняются при параллельном
переносе;
- пространство изотропно, т. е. свойства
пространства не зависят от направления; другими
словами - свойства не меняются при повороте.
Электрический заряд.
Так же, как масса частиц (тел малых
размеров по сравнению с расстояниями между ними)
определяет гравитационное взаимодействие и
проявляется именно во взаимодействии между
частицами, электрический заряд
проявляется во взаимодействии между зарядами.
Существуют два рода зарядов - положительный и
отрицательный, так что одноименные заряды
отталкиваются, а разноименные - притягиваются.
Будем считать, что система неподвижных
точечных зарядов частиц замкнута,
электрически изолированна, тогда справедлив
закон сохранения электрических зарядов:
в изолированной системе зарядов их
алгебраическая сумма неизменна во времени.
Электрическое поле неподвижных
зарядов.
Физический вакуум обеспечивает взаимодействие
зарядов, т. е. обладает электрическими
свойствами: его особое электрическое состояние
возникает в присутствии электрического заряда,
так что другой заряд, помещенный в такое
пространство, испытывает воздействие некоторой
силы. Особое электрическое состояние
пространства, проявляющееся в том, что на другой,
"пробный" заряд в любой точке вакуума
действует сила, называется электрическим
полем.
Создающий поле заряд точно так же находится в
поле пробного заряда и точно так же испытывает
силовое воздействие. В каждой точке физического
вакуума результирующее состояние -
электрическое поле - есть простая векторная
сумма полей двух взаимодействующих зарядов: поля
зарядов просто "налагаются", "не
замечая" друг на друга. Это - формулировка
принципа наложения (суперпозиции) полей
электрических зарядов.
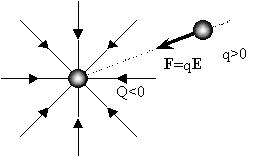
Попробуем геометрически представить
простейшее электрическое поле - поле уединенного
точечного неподвижного электрического заряда:
а) в силу однородности пространства
конфигурация поля не зависит от координат
заряженной частицы;
б) в силу изотропности пространства
конфигурация поля одинакова во всех
направлениях: поле обладает сферической
симметрией, т. е. линии, вдоль которых
направлена сила действия на пробный заряд
(силовые линии), образуют сферически (центрально-)
симметричную систему прямых (как иглы
морского ежа), начинающихся на заряде Q и уходящих
в бесконечность:
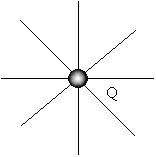
в) свяжем направленность силовых линий
с направлением действия на положительный
пробный заряд, а густоту, т. е.
количество силовых линий через 1 м2
перпендикулярной силовым линиям плоскости - с
уровнем интенсивности поля заряда Q в данной
области, т. е. с величиной, численно равной силе,
действующей на единичный положительный заряд
или напряженностью электрического поля.
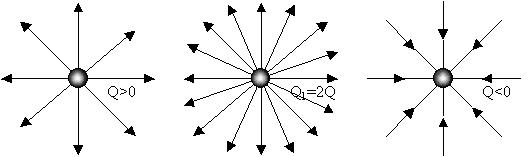
Замечание. Внесение единичного заряда
может заметно исказить поле заряда Q в силу
принципа суперпозиции:
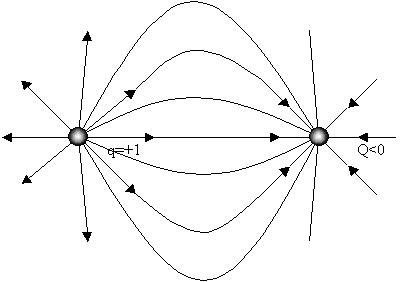
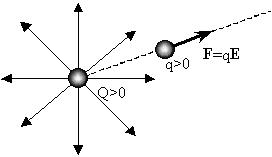
Поэтому на опыте вектор напряженности поля E
заряда Q находят как отношение вектора силы F,
действующей на малый ("практически не
искажающий" поле) заряд q, к величине этого
пробного заряда:
E = F/q .
Поток вектора электрического поля Е.
Рассмотрим небольшую область электрического
поля, силовые линии которого пересекают часть
плоскости  S
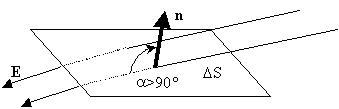
под некоторым углом a к вектору n,
перпендикулярному к плоскости (|n|=1): S
под некоторым углом a к вектору n,
перпендикулярному к плоскости (|n|=1):
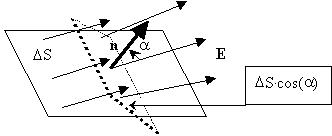
Такой вектор n называется вектором нормали
к поверхности.
Будем считать, что в рассматриваемой малой
области поля силовые линии параллельны друг
другу и их густота везде одинакова: Е=const
(такое поле называется однородным).
Проведем через основание вектора нормали
плоскость, перпендикулярную Е. Спроектируем
поверхность  S на построеннную плоскость вдоль
силовых линий. Очевидно, площадь проекции
составит S на построеннную плоскость вдоль
силовых линий. Очевидно, площадь проекции
составит  Scos( Scos(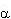 ). Если вспомнить
условие, что напряженность поля выражается
густотой силовых линий, т. е. численно равна их
количеству через единицу площади,
перпендикулярной силовым линиям плоскости, то
всего такую площадку, а значит и площадку ). Если вспомнить
условие, что напряженность поля выражается
густотой силовых линий, т. е. численно равна их
количеству через единицу площади,
перпендикулярной силовым линиям плоскости, то
всего такую площадку, а значит и площадку  S,
пересекут S,
пересекут 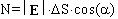 силовых
линий. Это число силовых линий называется
потоком силовых
линий. Это число силовых линий называется
потоком  ФЕ вектора Е через поверхность ФЕ вектора Е через поверхность  S: S:
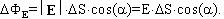
Поток поля может быть и отрицательным при 270 > >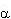 >90 >90
В случае поля произвольной конфигурации и
поверхности произвольной формы нужно разбить
поверхность на m малых плоских областей так,
чтобы в пределах каждой такой i-той области поле Еi можно было считать однородным, и найти
сумму (интеграл) всех i-тых потоков:
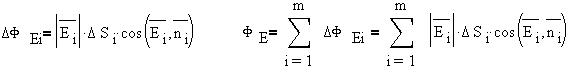
Для немногих симметричных полей можно выбрать
поверхность аналогичной симметрии так, чтобы
везде на ней модуль вектора напряженности
электрического поля и угол между полем и
нормалью были постоянными, а в скобках останется
просто сумма площадей участков поверхности.
Теорема Гаусса для электрического
поля.
Поток силовых линий через поверхность играет
роль меры на образе поля. Чтобы получить
некий закон с помощью такой меры, нужно
выбрать общий тип поверхности, а именно - замкнутую
поверхность (которая, очевидно, состоит из
участков незамкнутых поверхностей и
представляет собой нечто "большее", более
общее). Договоримся вектор нормали направлять
наружу замкнутой поверхности, - тогда
"входящие" извне силовые линии образуют
отрицательный поток, а "выходящие" изнутри
силовые линии образуют положительный поток.
Очевидно, здесь могут быть две ситуации:
а) внутри поверхности заряды отсутствуют, тогда
силовые линии полей внешних зарядов,
пронизывающие насквозь замкнутую поверхность,
создадут "входящий" отрицательный
поток и точно такой же по модулю "выходящий"
положительный поток (ведь геометрический
смысл потока - просто количество силовых линий!),
так что суммарный поток будет нулевым:
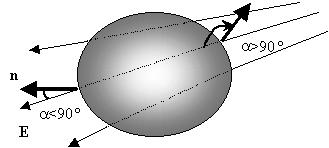
б) внутри замкнутой поверхности находятся
электрические заряды, тогда их поля, согласно
принципу суперпозиции, просто складываются, и
общее количество силовых линий, "выходящих"
наружу, прямопропорционально количеству k
зарядов внутри поверхности (поток иголок сквозь
полиэтиленовый пакет прямопропорционален
количеству ежей в пакете):
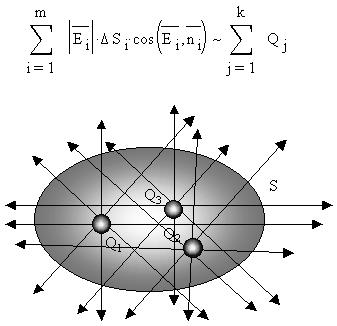
Очевидно, за интенсивность поля (густоту
силовых линий) данного заряда "отвечает" и
физическая среда, в которой он находятся. В
вакууме коэффициент пропорциональности между
потоком поля сквозь замкнутую поверхность и
количеством зарядов внутри нее образован
фундаментальной электрической постоянной 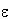 0: 0:
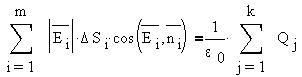
В диэлектрике за счет противоположного поля
поверхностных зарядов поле "внедренного"
заряда ослабевает в 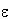 раз:
раз:
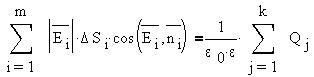
Полученное выражение носит название теорема
Гаусса. В общем случае, рассматриваемом
разделом высшей математики - классической
теорией поля, формулировка теоремы следующая: поток
вектора поля сквозь замкнутую поверхность
прямопропорционален количеству источников поля
внутри поверхности. Поле при этом может быть
любой природы: гравитационное, магнитное и т. п.
Расчет симметричных полей.
Теорема Гаусса, в случае симметричных полей
(когда Е и cos(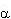 ) можно
вынести за скобку), применяется для нахождения
закона (формулы) напряженности электрического
поля неподвижных зарядов (электростатического
поля) как функции суммарного заряда (назависимо
от его способа распределения внутри поверхности),
координат и свойств физической среды. ) можно
вынести за скобку), применяется для нахождения
закона (формулы) напряженности электрического
поля неподвижных зарядов (электростатического
поля) как функции суммарного заряда (назависимо
от его способа распределения внутри поверхности),
координат и свойств физической среды.
1. Поле точечного заряда.
Как мы уже видели, поле такого заряда имеет
сферическую (центральную) симметрию, и если
выбрать такого же типа симметрии поверхность,-
сферу с центром, совпадающим с зарядом, - то везде
на сфере, в силу равноудаленности её поверхности
от заряда, модуль напряженности поля будет
постоянным, а угол между вектором напряженности
и вектором нормали к поверхности равен 0, так как
оба направлены по радиусу сферы:
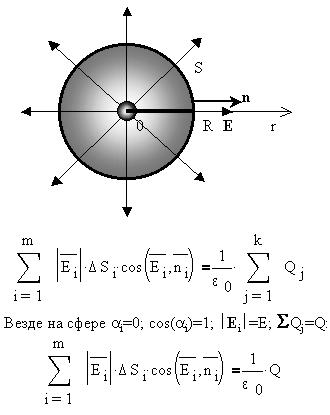
а сумма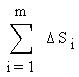 есть
просто поверхность сферы радиуса R, равная 4pR есть
просто поверхность сферы радиуса R, равная 4pR : :
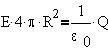
откуда находим формулу напряженности поля
точечного заряда:
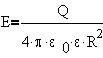
Полученая формула носит название закон
Кулона для точечного заряда. Как видим,
наличие множителя 4pR связано
с центральной симметрией поля (вследствие
изотропности физического пространства). связано
с центральной симметрией поля (вследствие
изотропности физического пространства).
2. Поле равномерно заряженного шара.
Введем понятие объемной плотности заряда 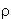 , численно равной заряду единицы
объема: , численно равной заряду единицы
объема:
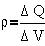
Пусть радиус шара равен R, полный заряд шара
равен Q и 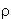 =const. Вне и внутри шара
поле, очевидно, буде сферически симметричным,
поэтому в качестве замкнутых поверхностей
выбираем две концентрические сферы радиусами R1 меньше и R2 больше R с
центрами в центре шара: =const. Вне и внутри шара
поле, очевидно, буде сферически симметричным,
поэтому в качестве замкнутых поверхностей
выбираем две концентрические сферы радиусами R1 меньше и R2 больше R с
центрами в центре шара:
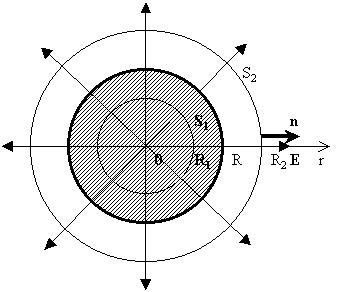
Внутри поверхности S2 радиуса R2 сосредоточен полный заряд шара Q, так
что поле вне шара, как это следует из теоремы
Гаусса, идентично полю точечного заряда Q,
помещенного в центр шара:
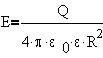
Внутри же внутренней сферы S1
радиуса R1 сосредочен заряд, равный
произведению объемной плотности заряда на объем
сферы:
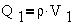
где
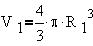
Полный заряд шара Q и заряд внутреннего объема
радиуса R1 Q1 соотносятся
как кубы радиусов:
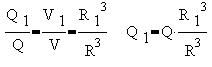
Подставим выражение для Q1 в
теорему Гаусса:
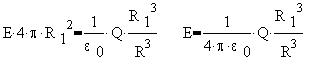
Для построения в MathCAD6.0PLUS графика зависимости
напряженности поля от расстояния от центра шара
примем Q=4p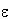 0
Кл и R=1 м 0
Кл и R=1 м
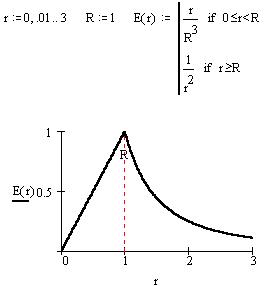
3. Поле равномерно заряженной
бесконечной плоскости.
Введем понятие поверхностной плотности заряда 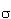 >0, численно равной заряду
единицы площади: >0, численно равной заряду
единицы площади:
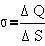
В силу однородности и изотропности
пространства силовые линии поля равномерно
заряженной бесконечной плоскости должны быть
перпендикулярными к ней и иметь равномерную
густоту, что соответствует определению
однородности поля Е=const. В качестве
"удобной" замкнутой поверхности выберем
прямой цилиндр, боковая поверхность которого
параллельна силовым линиям (везде на ней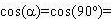 0 и, следовательно,
поток сквозь нее равен 0), а торцевые поверхности
площадью S - параллельны заряженной плоскости
(так что везде на них 0 и, следовательно,
поток сквозь нее равен 0), а торцевые поверхности
площадью S - параллельны заряженной плоскости
(так что везде на них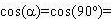 1): 1):
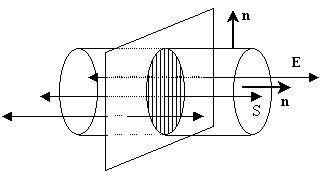
Поток однородного поля Е сквозь обе
перпендикулярные ему торцевые поверхности S
равен просто Е2S, а заряд, сосредоточенный на
участке площадью S заряженной поверхности, равен 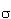 S: S:
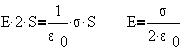
4. Поле двух бесконечных параллельных
разноименно заряженных плоскостей.
Однородные поля таких плоскостей будут
отличаться лишь направленностью силовых линий
(модули поверхностных плотностей заряда
одинаковы):
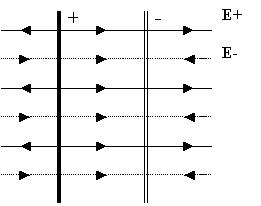
Из рисунка видно, что вне области между
плоскостями их поля взаимно "погашаются", и
внутри - суммируются:
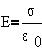
Циркуляция вектора поля Е.
Плоскость, которую пронизывает поток силовых
линий, служит одновременно и некоторым
"индикатором" наличия поля в данной области
пространства. Однако отсутствие потока не всегда
означает отсутствие поля: силовые линии могут
просто "лежать" в плоскости и угол между
векторами E и n составит 90 . Дополнительным "портретом" поля, т.е. .мерой,
отражающей его интенсивность и направленность,
может служить в данной точке - проекция
вектора Е на некоторое направление, а в
пространстве плоскости - сумма произведений
перемещений на проекции вектора напряженности
поля на направление этих перемещений. Ближайшая
механическая аналогия - подсчет работы некоторой
силы. Причем в случае вектора напряженности
электрического поля физический смысл аналогии
сохраняется: напряженность численно равна силе,
действующей на единичный заряд, а сумма
произведений проекций напряженности на
перемещения численно равна работе поля при
перемещении единичного заряда (+1 Кл). . Дополнительным "портретом" поля, т.е. .мерой,
отражающей его интенсивность и направленность,
может служить в данной точке - проекция
вектора Е на некоторое направление, а в
пространстве плоскости - сумма произведений
перемещений на проекции вектора напряженности
поля на направление этих перемещений. Ближайшая
механическая аналогия - подсчет работы некоторой
силы. Причем в случае вектора напряженности
электрического поля физический смысл аналогии
сохраняется: напряженность численно равна силе,
действующей на единичный заряд, а сумма
произведений проекций напряженности на
перемещения численно равна работе поля при
перемещении единичного заряда (+1 Кл).
Рассмотрим область поля положительного
точечного заряда.
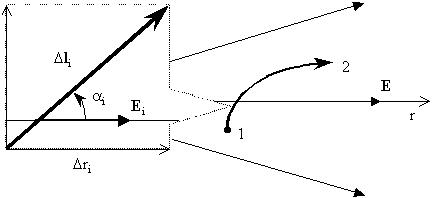
На некотором i-том участке перемещения  li
(столь малом, что его можно считать линейным)
общего перемещения единичного точечного заряда
из точки 1 в точку 2 поля E в пересчете на +1 Кл
совершена элементарная работа li
(столь малом, что его можно считать линейным)
общего перемещения единичного точечного заряда
из точки 1 в точку 2 поля E в пересчете на +1 Кл
совершена элементарная работа  Ui, равная Еi Ui, равная Еi licos( licos(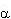 i).
При этом i).
При этом  licos( licos(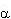 i)= i)= ri,
равное проекции вектора элементарного
перемещения ri,
равное проекции вектора элементарного
перемещения  li на направление поля Е.
При бесконечно малом перемещении li на направление поля Е.
При бесконечно малом перемещении
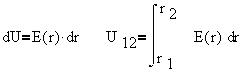
Можно сделать вывод, что при перемещении по
траектории любой формы работа полем (или над
полем) совершается постольку, поскольку
происходит движение по силовой линии, вдоль
поля (или против поля). Какой бы сложной ни
была форма траектории при перемещении заряда от
точки 1 в точку 2, работа в перпендикулярных
силовым линиям направлениях всегда равна нулю
(cos(90 )=0), а работы на
"поступательно-возвратных" участках
взаимно компенсируют друг друга (косинус меняет
знак). )=0), а работы на
"поступательно-возвратных" участках
взаимно компенсируют друг друга (косинус меняет
знак).
В частности при возврате в исходную точку 1
суммарная работа равна нулю: суммарная
положительная работа поля компенсирована
суммарной отрицательной работой внешних сил
против поля. Так как замкнутая линия состоит из
незамкнутых участков, то ее форма имеет более
общий характер и "годится как объект для
теоремы": циркуляция вектора Е вдоль
замкнутой траектории тождественно равна нулю ("циркуляция"
- это как разсумма произведений перемещений
на проекции вектора напряженности поля на
направление этих перемещений по всей замкнутой
траектории):
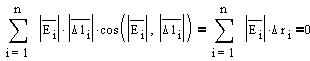
Пример 1.Возможна ли приведенная на
рисунке ниже конфигурация электростатического
поля?
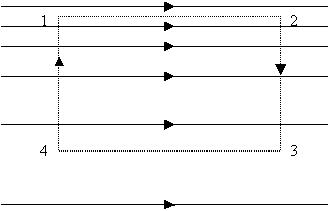
Нет, невозможна. На участках обхода 2 - 3 и 4 - 1,
перпендикулярных вектору поля, вклад в
циркуляцию равен нулю. На участке 1 - 2 вклад
положителен, на участке 3 - 4 -отрицателен, но так
как на этих участках напряженность поля (густота
силовых линий) различна, то суммарная циркуляция
поля при обходе прямоугольника не равна 0, что
противоречит теореме о циркуляции.
Пример 2. Могут ли силовые линии
электростатического поля быть замкнутыми?
Нет, так как при этом циркуляция вектора поля,
подсчитанная, например, вдоль силовой линии
(косинус угла между вектором напряженности и
направлением обхода всегда равен +1), не равна
нулю.
Поля, силовые линии которых замкнуты,
называются вихревыми. В них, в частности,
сумма произведений вектора поля на направления
обхода зависит от формы траектории, как это видно
из сравнения двух траекторий от точки 1 в точку 2
на рисунке:
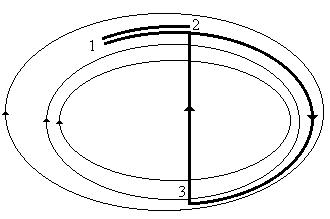
Независимость работы от формы траектории или
нулевая циркуляция вектора поля - признак консервативности
электрического поля неподвижного заряда. Ясно,
что стационарные поля любых центральных
(сферически симметричных) сил, например,
гравитационной, являются консервативными.
Потенциал электростатического поля Е.
Величина, численно равная работе поля
точечного заряда Q по переносу единичного
положительного заряда из точки 1 в точку 2, или электрическое
напряжение, равна:
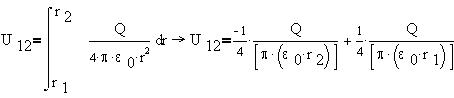
Или, в более удобном виде:
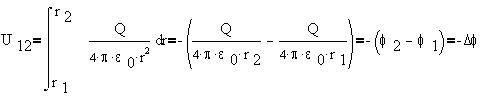
Скалярные величины 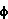 1 и 1 и 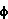 2 численно равны работе
против поля по переносу единичного
положительного заряда из бесконечности (где поле
точечного заряда Q отсутствует, равно 0) в точки,
находящиеся на расстояниях r1и r2 от заряда Q,
например: 2 численно равны работе
против поля по переносу единичного
положительного заряда из бесконечности (где поле
точечного заряда Q отсутствует, равно 0) в точки,
находящиеся на расстояниях r1и r2 от заряда Q,
например:
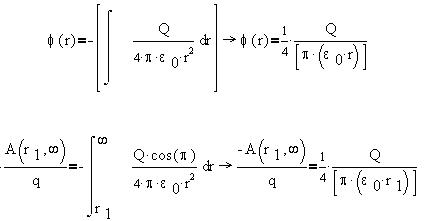
Здесь  - угол междувекторами
поля и перемещения против поля. - угол междувекторами
поля и перемещения против поля.

Величина, численно равная работе поля
точечного заряда Q по переносу +1 Кл из из точки 1 в
бесконечность:
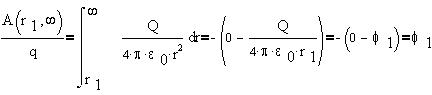
Здесь 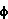 1
количественно равен убыли энергии единичного
положительного заряда до 0, равной уровню
потенциальной энергии +1 Кл в точке 1 или потенциалу
поля на расстоянии r1 от заряда Q. 1
количественно равен убыли энергии единичного
положительного заряда до 0, равной уровню
потенциальной энергии +1 Кл в точке 1 или потенциалу
поля на расстоянии r1 от заряда Q.
График напряженности и потенциала поля
точечного заряда 
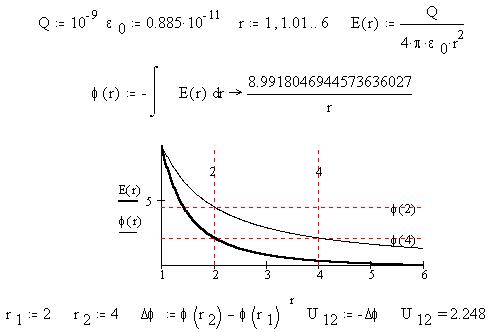
В консервативном поле работа поля (или против
поля) однозначно определена потенциалами поля в
начальной и конечной точках перемещения, точнее -
их разностью. Поэтому начальный, нулевой уровень
отсчета потенциала не обязательно связывать с
областью отсутствия поля. Например, для поля
бесконечной равномерно заряженной плоскости
условный 0 потенциала может быть определен на
самой плоскости. В технике же таким условным
нулем принимают потенциал поверхности Земли.
Если объединить в поверхность все точки
равного потенциала, т. е. образовать
эквипотенциальную поверхность, то, очевидно, при
перемещении зарядов по ней работа будет нулевой.
Геометрически это означает перпендикулярность
силовых линий к поверхности. Можно сказать, что
для расчета симметричных полей с помощью теоремы
Гаусса мы выбирали именно эквипотенциальные
поверхности. Итак, поле перпендикулярно
эквипотенциальной поверхности. С другой стороны,
ясно, что потенциал поля меняется быстрее всего
вдоль силовой линии (изменение потенциальной
энергии +1 Кл в результате работы в направлении
действия силы):
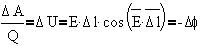
Если условиться проводить эквипотенциальные
поверхности через одинаковое изменение
потенциала (например, 1 В), то, как это видно из
приведенной выше формулы, интенсивность поля
также будет определяться на графике густотой
эквипотенциальных поверхностей (на 1 м силовой
линии).
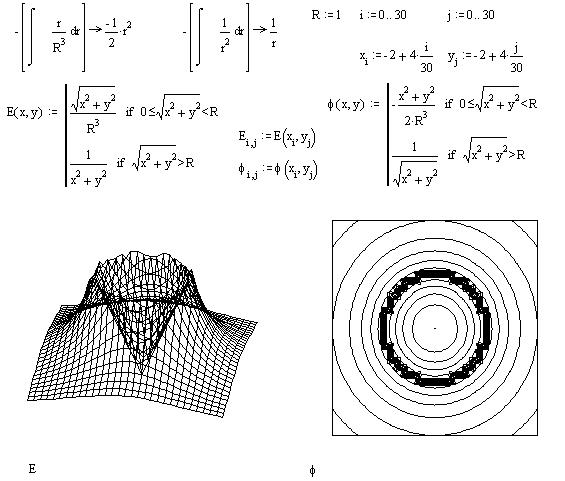
Поверхностный график напряженности и линии
уровня потенциала поля равномерно заряженного
шара:
Электроемкость уединенного
проводника.
Электроемкость уединенного проводника - это
физическая величина, численно равная заряду,
необходимoму для повышения потенциала
проводника на 1 В:
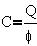
Найдем емкость проводника формой шара радиуса
R:
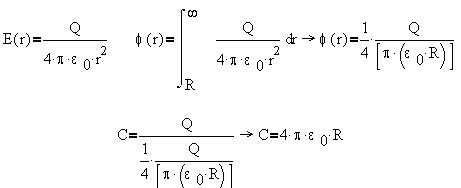
Найдем размер шара емкостью 1Ф:
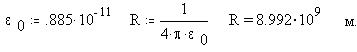
При этом емкость шара размером в земной равна:
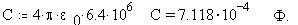
Избыточный заряд величиной 1 Кл поднял бы
потенциал такого шара на
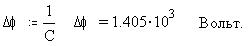
Как видим, емкость проводника определена его
"габаритами". Совершенно аналогично,
"энергетическая емкость" бочки, т. е.
величина, численно равная массе воды,
необходимой для повышения ее потенциала в поле
тяжести на единицу (в однородном поле тяжести на
высоте h потенциал численно равен потенциальной
энергии 1 кг: gh), прямопропорциональна площади дна
бочки.
Диэлектрик в e раз ослабляет поле и,
следовательно, в 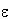 раз увеличивает емкость.
раз увеличивает емкость.
Электроемкость плоского конденсатора.
Так как знак потенциала точечного заряда
совпадает со знаком самого заряда, то
индуцирование в близлежащих телах зарядов
противоположного знака приводит к уменьшению
потенциала "индуцирующего" заряда, что,
соответственно, означает увеличение
электроемкости системы близлежащих тел,
получившей название конденсатор.
Плоский конденсатор представляет из себя две
плоские пластины, расстояние между которыми d
мало по сравнению с их линейными размерами. Это
предположение позволяет пренебречь малыми
областями неоднородности электрического поля у
краев пластин и считать, что все поле однородно и
сосредоточено между пластинами. Заряд
конденсатора Q - это заряд положительно
заряженной пластины.
Емкость конденсатора определяется как
величина, численно равная заряду, необходимому
для изменения разности потенциалов пластин,
напряжения U между обкладками, на 1 В:
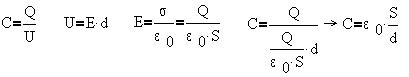
Заполнение пространства между пластинами
диэлектриком, очевидно, увеличит емкость в 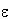 раз. раз.
Емкость системы конденсаторов.
Параллельное соединение конденсаторов
соответствует простому увеличению площади
обкладок, так что емкость системы равна сумме
емкостей отдельных конденсаторов.
При последовательном соединении заряды всех
конденсаторов одинаковы и равны заряду всей
системы, а общее напряжение равно сумме
напряжений отдельных конденсаторов,
обратнопропорциональных их емкостям, так что
складыватся величины, обратные емкостям:
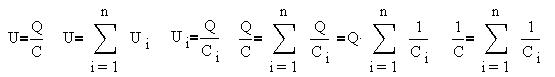
Можно показать, что при таком соединении
емкость системы меньше самой малой отдельной
емкости.
Энергия электрического поля.
1. Энергия взаимодействия точечных
зарядов.
Перенесем положительный заряд Q2 из
бесконечности на расстояние R от положительного
заряда Q1. Если заряды разноименны, то
направление переноса сменим на противоположное,
- лишь бы работа по переносу одного заряда
производилась против поля другого заряда и тем
самым превратилась в потенциальную энергию
образованной системы зарядов.
В результате произведенной работы заряд Q2 оказался в точке с потенциалом 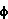 1 поля
заряда Q1, и его потенциальная
энергия равна: 1 поля
заряда Q1, и его потенциальная
энергия равна:
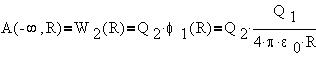
Точно такую же работу надо было бы совершить
при переносе заряда Q1 в поле заряда Q2. Иными словами, в системе отсчета,
связанной с зарядом Q2 эта же работа
равна:
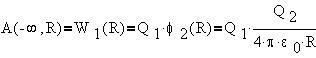
Энергия системы зарядов оказывается равной
полусумме потенциальных энергий обоих зарядов:
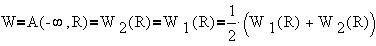
В общем случае n точечных зарядов каждый i-й
заряд обладает потенциальной энергией в
суммарном поле остальных зарядов, и полная
энергия всей системы есть полусумма
потенциальных энергий всех зарядов:
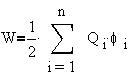
Здесь 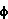 i
- суммарный потенциал поля зарядов,
взаимодействующих с Q i. i
- суммарный потенциал поля зарядов,
взаимодействующих с Q i.
Пример. Найдем энергию взаимодействия
четырех одинаковых положительных зарядов Q,
закрепленных в вершинах тетраэдра с ребром,
равным а.
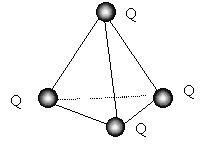
Три заряда создают в точке нахождения i-го
четвертого поле с суммарным потенциалом 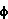 i, равным i, равным
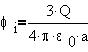
Полная энергия системы четырех зарядов равна:
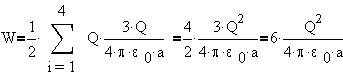
Ответ можно интерпретировать и так: энергия
системы зарядов равна сумме энергий 6 пар
взаимодействующих зарядов.
2. Энергия заряженного проводника.
Заряд Q проводника рассредоточен по его
поверхности с потенциалом 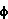 , так что энергия такого заряда равна: , так что энергия такого заряда равна:
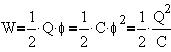
3. Энергия поля конденсатора.
Учитывая, что заряды обкладок противоположны
по знаку, получим:
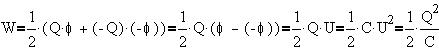
4. Энергия электрического поля.
Формулу энергии поля конденсатора можно также
получить, осуществив мысленный эксперимент по
перемещению обкладки плоского конденсатора
в однородном поле другой обкладки E1
на расстояние d:
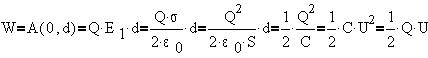
Интересно провести преобразования так, чтобы в
формуле фигурировали напряженность поля
конденсатора Е=2E1 и его
геометрические размеры:
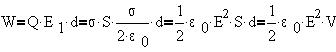
Полученная формула показывает, что энергия
электрического поля рассредоточена по всему
объему, занимаемому полем, с плотностью
энергии, равной:
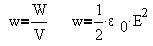
Здесь видно, что w численно равна энергии
единицы объема поля.
При наличии в области поля диэлектрика
плотность энергии и полная энергия поля
возрастают в 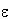 раз
(дополнительный заряд для компенсации поля
поверхностного заряда диэлектрика): раз
(дополнительный заряд для компенсации поля
поверхностного заряда диэлектрика):
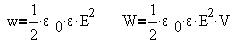
Постоянный ток.
Электрический ток представляет собой процесс
переноса заряда через некоторую поверхность,
например - через поперечное сечение проводника.
За направление электрического тока принимается
направление, в котором дрейфуют с некоторой
средней скоростью положительные носители
заряда.
Количественной мерой электрического тока
служит физическая величина, численно равная
заряду, проносимому через некоторую поверхность
(например, поперечное сечение проводника) в
единицу времени:

В случае постоянного тока происходит
стационарное, неизменное во времени перемещение
заряда. Пространственное распределение
электрических зарядов неизменно: дрейфующие
заряды заменяются новыми. Электрическое
кулоновское поле движущихся зарядов остается
потенциальным. Но упорядоченное движение
зарядов означает, что, в отличие от
электростатической ситуации, в проводнике есть
постоянное электрическое поле.
Условный положительный заряд перемещается по
полю: от высокого потенциала к низкому
(отрицательно заряженные носители заряда в
проводнике - электроны - движутся в
противоположном направлении). Количество заряда
в единицу времени прямопропорционально
величине, численно равной работе поля над +1 Кл:
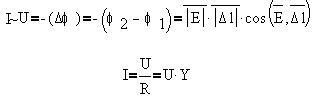
Мы записали закон Ома для однородного участка
электрической цепи. Здесь R - электрическое
сопротивление проводника, Y - электрическая
проводимость участка,- величина, обратная
сопротивлению.
Соединения сопротивлений.
Общим методом решения задач на определение
параметров электрических цепей является
применение двух законов сохранения
(электрического заряда и энергии) и основного
закона причинно-следственной связи (закон Ома,
связывающий величину силы тока с работой
электрического поля на участке цепи, которая
определяется напряженностью поля). В механике
аналогично применяются законы сохранения
(энергии и импульса, например) и второй закон
Ньютона.
1. Последовательное соединение
сопротивлений.
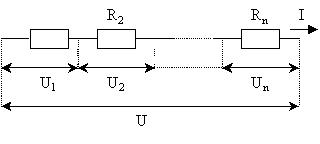
Величина, численно равная полной работе поля
над +1 Кл или напряжение, равна сумме напряжений
на участках R1, R2,... Rn:
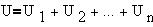
Учитывая закон Ома для отдельных участков и
всего соединения, а также постоянство силы тока
по всем участкам, имеем:
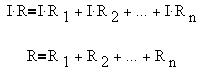
2. Параллельное соединение
сопротивлений.
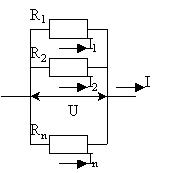
Напряжение на всех участках соединения
одинаково, а общая сила тока равна сумме токов
отдельных участков. С учетом закона Ома для всей
цепи и отдельных участков, запишем:
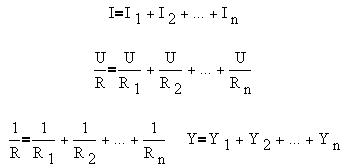
Обобщенный закон Ома для
неоднородного участка цепи.
Кроме поля кулоновских сил на участке цепи
может присутствовать источник поля так
называемых "сторонних сил", не кулоновских,
которое обеспечивает движение положительного
заряда от низкого потенциала к высокому, против
кулоновского поля. Участок электрической цепи,
включающий такой источник, называется
неоднородным. Величина, численно равная работе
поля сторонних сил над + 1 Кл при перемещении
заряда внутри источника от меньшего потенциала к
большему называется электродвижущей силой (ЭДС).
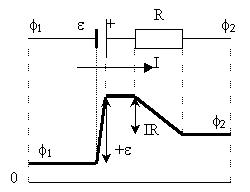
Как видно из рисунка, величина, численно равная
полной работе над +1Кл на всем неоднородном
участке, равна:
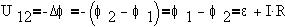
ЭДС - величина алгебраическая: в нашем примере
она записана со знаком "+", поскольку
повышает потенциал в направлении обхода
участка электрической цепи. Точно так же со
знаком "+" записано произведение IR в силу
того, что направление электрического тока
совпадает с направлением обхода: мы проходим
однородный участок с сопротивлением R в
направлении понижения потенциала (в направлении
электрического поля).
Замечание. Выше полагалось, что
внутреннее сопротивление ЭДС равно нулю. В
противном случае на его величину r увеличилось бы
сопротивление всего участка: 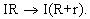
Правила Кирхгофа для разветвленных
цепей.
1. Учет закона сохранения
электрического заряда (первое правило Кирхгофа).
В любом узле электрической цепи сумма входящих
и выходящих токов равна нулю:
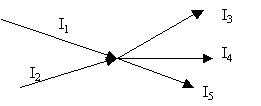
Если условиться входящие токи записывать со
знаком "+", а выходящие - со знаком "-", то
для узла на рисунке имеем:
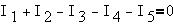
Для N узлов электрической схемы можно записать
N-1 независимых уравнений, так как токи,
формирующие N-й узел входят в уже расмотренные
узлы, и уравнение для N-го узла есть комбинация
других уравнений (иными словами, уравнение для
N-го узла не содержит "новых" неизвестных).
Токи в ветвях цепи можно направлять
произвольным образом: в случае неправильно
"угаданного" направления в результате
расчета величина соответствующего тока
получится отрицательной, и останется лишь
поменять направление тока на схеме.
2. Учет закона сохранения энергии и
основного закона причинно-следственной связи
(второе правило Кирхгофа).
Рассмотрим отдельный контур электрической
цепи, составленный, например, из четырех
неоднородных участков:
При обходе контура, например, по часовой
стрелке, мы возвращаемся в исходный узел, так что
полная работа электрического кулоновского поля
над +1 Кл (циркуляция Е) равна нулю, а сумма
частичных работ на сопротивлениях Ui=IiRi должна равняться сумме
ЭДС, включенных в контур.
В самом деле, применим для четырех ветвей
контура обобщенный закон Ома с учетом знаков ЭДС
и напряжений на сопротивлениях:
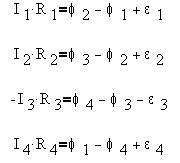
При проходе по часовой стрелке третьего
участка направление тока и направление
действия ЭДС - против направления обхода.
Сложив все четыре уравнения, получим:
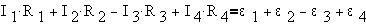
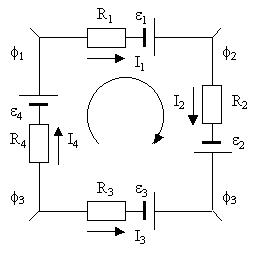
Пример. Найдем неизвестные токи в
предложенной на рисунке ниже электрической цепи,
считая, что численные значения сопротивлений и
ЭДС просто совпадают с их номерами в схеме.
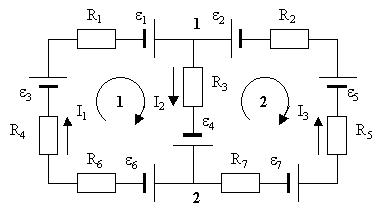
В схеме три ветви и три неизвестных тока. Для
двух узлов имеем одно независимое уравнение (те
же токи с обратными знаками составляют уравнение
для другого узла). Независимых контуров
(включающих не вошедшие в другие контуры ветви)
здесь два (столько же, сколько "ячеек" в
"плоской" схеме).
Замечание. Как варианты выбора
контуров, можно взять контур-периметр схемы и
любую из "ячеек"(1 или 2).
Запишем по первому правилу Кирхгофа уравнение
для узла 1:
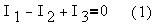
По второму правилу Кирхгофа запишем для
контуров 1 и 2 при их обходе по часовой стрелке:
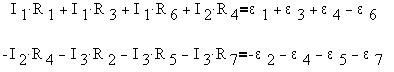
Или, с учетом численных значений сопротивлений
и ЭДС:
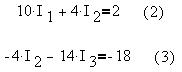
Выпишем матрицу коэффициентов при неизвестных,
вектор-столбец свободных членов системы
уравнений (1) - (3) и найдем в MathCAD 6.0 PLUS решение
системы:
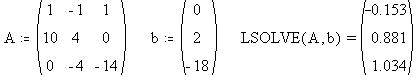
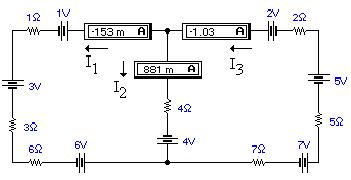
На схеме электрической цепи направление тока I1 необходимо поменять на
противоположное. Найденные токи равны: I1=0,153
А; I2=0,881 А; I3=1,034 А.
Электронная модель схемы в Electronics Workbench 4.0
подтверждает наши расчеты:
Закон Био-Савара- Лапласа.
1. Магнитное поле движущегося точечного
заряда.
Рассмотрим движущийся с постоянной скоростью
точечный положительный электрический заряд Q.
В окружающем пространстве электрическое поле
меняется как по величине, так и по направлению.
На изменение электрического состояния
физический вакуум "реагирует"
"противоположным" состоянием - магнитным.
Можно ожидать, во-первых, что интенсивность
такой реакции прямопропорциональна
интенсивности, скорости изменения вектора
электрического поля по величине и направлению
и, во-вторых, что возмущение "потревоженной"
среды расходится как круги на воде от гребка
веслом, т. е. представляет из себя некое
вихревое поле с замкнутыми силовыми линиями.
Представим две "мгновенные" фотографии
движущегося точечного заряда в точках 1 и 2
(физически стационарную картину движущегося
заряда можно смоделировать малым прямым
участком проводника с постоянным током, в
проводах подвода заряда к которому текут
противоположно направленные токи, и эффекты от
них взаимно компенсируются):
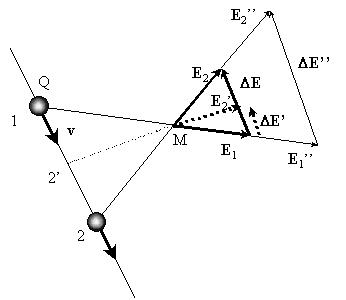
Модуль векторной величины, характеризующей
интенсивность магнитного поля и называемой магнитной
индукцией, прямопропорционален скорости
изменения вектора Е:
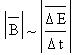
Скорость изменения Е, как это видно из
рисунка, определяется, во-первых, величиной
движущегося заряда - величиной вектора Е (Е''>E1,  E''> E''> E) и, во-вторых, скоростью движения
заряда: при скорости v'<v заряд попадает в
точку 2': угол между Е1 и Е'2 меньше угла между Е1 и Е2 и E) и, во-вторых, скоростью движения
заряда: при скорости v'<v заряд попадает в
точку 2': угол между Е1 и Е'2 меньше угла между Е1 и Е2 и  E'> E'> E. E.
Теперь учтем, что изменение электрического
поля по направлению нулевое по оси движения
заряда и максимальное - в перпендикулярной оси
движения и проходящей через заряд плоскости (в
силу изотропии пространства, в любом направлении
в этой плоскости), т. е. зависит, очевидно, от
синуса угла между v и Е:
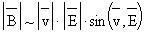
Коэффициент пропорциональности определяется и
электрическими, и магнитными свойствами
физического вакуума и равен произведению
электрической и магнитной постоянных:
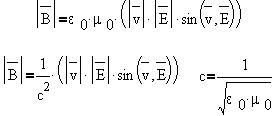
Электродинамическая постоянная с -
есть не что иное, как скорость распостранения
электромагнитных колебаний в вакууме.
Вектор индукции магнитного поля В
перпендикулярен вектору скорости движения
заряда v и вектору напряженности
электрического поля Е (линия вектора В
должна "выглядеть" одинаково в любом
направлении в плоскости, перпендикулярной оси
движения и определяемой углом между v и Е
и расстоянием до точки на этой плоскости, т. е.
линии магнитного поля должны лежать в
перпендикулярных вектору скорости плоскостях).
Результатом произведения векторов v и Е
стал перпендикулярный им вектор В, модуль
которого прямопропорционален синусу угла между
векторами-множителями, т. е. максимален при их
взаимной перпендикулярности. Такое произведение
векторов называется векторным (в отличие
от скалярного, равного произведению
модулей векторов на косинус угла как при расчете
работы):
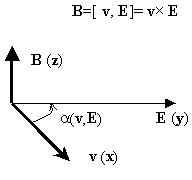
Векторы скорости v движения заряда,
напряженности E его электрического поля и
индукции B магнитного поля в точке М
пространства, очевидно, составляют
правовинтовую тройку (как привычная тройка
векторов x, y, z): если первый
сомножитель - вектор v поворачивать до
совмещения со вторым сомножителем -
вектором Е по часовой стрелке, то в
направлении произведения - вектора В
будет "вкручиваться" винт с правой резьбой.
Очевидно также, что перемена местами
сомножителей приведет к замене угла 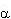 на угол 360 на угол 360 - -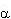 , так что синус
поменяет знак, а вектор-произведение станет
противоположно направленным. , так что синус
поменяет знак, а вектор-произведение станет
противоположно направленным.
Чтобы не ошибаться в порядке сомножителей,
можно воспользоваться следующим мнемоническим
правилом: вектор x - это вектор-причина,
которая всегда связана с изменением, движением
(скорость движущегося заряда, например), вектор y -
это вектор-обстоятельство в точке, где
действует причина (например, электрическое поле
на мгновенной фотографии), вектор z - это
вектор-результат действия причины в данных
обстоятельствах (например, вектор индукции
магнитного поля).
Пример. Построим силовую линию индукции
магнитного поля в случае, когда отрицательный
заряд пересекает плоскость чертежа
перпендикулярно ей в направлении от
наблюдателя (вектор скорости заряда покажем
в виде "крестика-оперения стрелки":
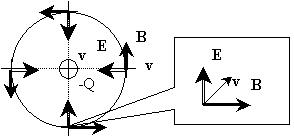
Учтем для стационарной конфигурации полей (или
для их мгновенной фотографии) закон Кулона:
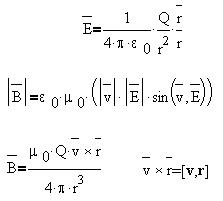
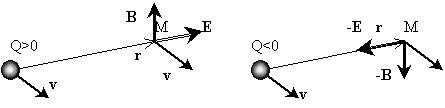
В таком представлении "обстоятельства",
связанные с точкой М пространства, определяются
ее расположением, заданным вектором r,
относительно заряда, знак которого учитывается:
Замечание. Очевидно, что правовинтовой
тип векторной тройки связан с выбором знака
электрического заряда. Если бы заряд электрона
"объявили" положительным, то в
электродинамике векторные тройки стали бы
левовинтовыми.
2. Магнитное поле проводника с током.
Произведение Qv ("движущийся заряд" как
mv - "движущаяся масса", импульс) в случае
потоков заряда в проводниках нуждается в замене.
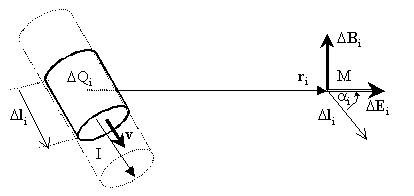
Выделим в тонком проводе малый фрагмент длиной  li
(вектор li
(вектор  li направлен в сторону тока), содержащий li направлен в сторону тока), содержащий  Qi
Кл, движущегося со средней скоростью v заряда.
Размер заряда близок к точечному. Исходя из
определения скорости и силы тока, имеем: Qi
Кл, движущегося со средней скоростью v заряда.
Размер заряда близок к точечному. Исходя из
определения скорости и силы тока, имеем:
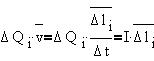
Произведение I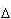 li
называется элемент тока, оно и заменяет
"движущийся заряд" во всех случаях перехода
от точечных зарядов к проводникам с током. li
называется элемент тока, оно и заменяет
"движущийся заряд" во всех случаях перехода
от точечных зарядов к проводникам с током.
Найдем магнитное поле, создаваемое этим
элементом тока в точке М:
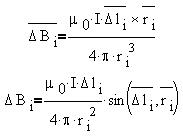
Чтобы найти полное магнитное поле в точке М,
нужно просуммировать поля, создаваемые всеми
элементами проводника:
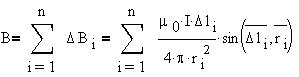
Пример. Найдем индукцию магнитного поля
в центре кругового витка с током.
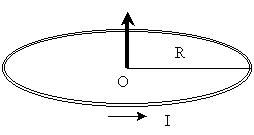
Очевидно, что везде на витке угол между
направлением тока I (касательной к витку) и
направлением на центр витка O постоянен и равен 90 , синус его равен 1. Расстояние от
любого элемента тока до центра витка также
постоянно и равно радиусу витка R. В скобках
остается лишь сумма длин , синус его равен 1. Расстояние от
любого элемента тока до центра витка также
постоянно и равно радиусу витка R. В скобках
остается лишь сумма длин 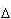 li элементов проводника, равная,
очевидно, длине окружности: li элементов проводника, равная,
очевидно, длине окружности:
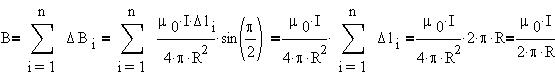
Теорема Гаусса для вектора В.
В силу замкнутости линий вихревого магнитного
поля поток вектора индукции сквозь любую
замкнутую поверхность тождественно равен нулю.
Теорема о циркуляции вектора В.
Поскольку магнитное поле создается токами, а
ненулевая циркуляция означает, что косинус угла
между вектором поля и векторами перемещений
преимущественно не меняет знак (т. е. перемещения
происходят преимущественно вдоль или против
силовых линий), то в этом случае замкнутый контур
обхода пронизывают создающие поле, направленное
вдоль (или против) направления обхода, токи,
алгебраическая сумма которых не равна нулю. Ток
считается положительным, если его направление
связано с направлением обхода правилом правого
винта:
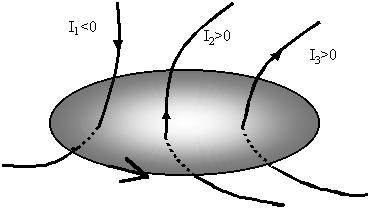
Циркуляция вектора индукции магнитного поля
прямопропорциональна алгебраической сумме
пронизывающих контур токов; коэффициентом
пропорциональности служит магнитная постоянная,
умноженная на магнитную проницаемость 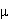 среды, которая в результате
намагничивания в среды, которая в результате
намагничивания в 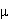 раз изменяет результирующее поле:
раз изменяет результирующее поле:
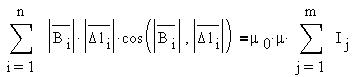
Замечание. В случае симметричных полей
теорема о циркуляции играет такую же роль в
расчете вектора индукции, какую в случае
симметричных электростатических полей играла
теорема Гаусса.
Пример 1. Найдем магнитное поле внутри и
снаружи бесконечно длинного прямого провода
круглого сечения. Ток I в проводе постоянный.
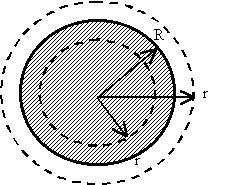
Из соображений симметрии ясно, что магнитное
поле будет обладать цилиндрической симметрией,
линии вектора поля образуют окружности с центром
на оси провода, а модуль вектора индукции будет
одинаков на том же расстоянии от центра. За
контур выберем окружность. Везде на контуре угол
между Вi и  li равен
нулю. li равен
нулю.
Сквозь наружный контур проходит ток провода I:
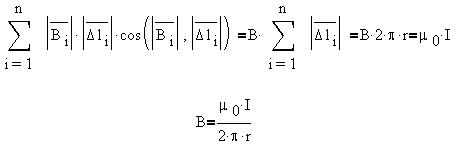
Отношение тока, пронизывающего внутренний
контур, и полного тока провода, очевидно, равно
отношению площадей поперечных сечений контура и
провода:
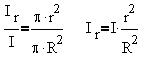
Применив теорему о циркуляции, имеем:
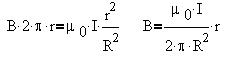
Представим полученные формулы на графике:
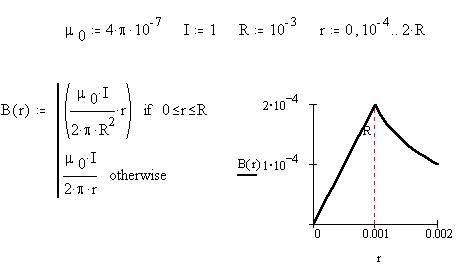
Пример 2. Найдем магнитное поле
соленоида.
Соленоидом называют обмотку из провода на
цилиндре. Тонкий провод (малый шаг спирали
обмотки) позволяет каждый виток представить в
виде кругового, а также пренебречь толщиной
провода:
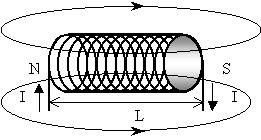
В случае длинного соленоида области
неоднородности поля на торцах соленоида можно не
учитывать, иными словами поле вне соленоида
отсутствует, а внутри оно однородно и
представляет сумму полей витков с током.
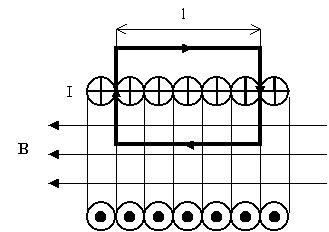
Учитывая геометрию однородного поля, за контур
обхода выберем прямоугольник, две стороны
которого параллельны силовым линиям. Ясно, что
внутри соленоида циркуляция В равна нулю, так
что выберем контур как на рисунке. Вне соленоида
поле отсутствует, внутри соленоида на отрезках,
перпендикулярных полю, косинус угла между полем
и перемещениями везде 0. На отрезке, параллельном
однородному полю, угол между полем и
перемещениями везде равен 0, так что вклад в
циркуляцию этого участка обхода равен:
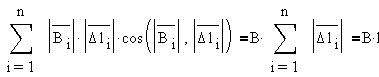
Пусть при общей длине соленоида L общее число
витков N, тогда плотность намотки, численно
равная числу витков на 1 м длины соленоида,
составит:
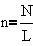
Число витков с током, охватываемых контуром,
равно nЧl и в каждом течет ток I. Итого, теорема о
циркуляции дает:
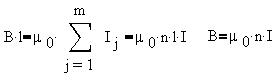
Если объем соленоида заполнен магнетиком с
магнитной проницаемостью 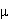 , то
индукция магнитного поля изменяется в , то
индукция магнитного поля изменяется в 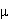 раз. раз.
Индуктивность.
Соленоид со своим однородным магнитным полем
аналогичен плоскому конденсатору с однородным
электрическим полем.
Напряженность электрического поля отражает
плотность заряда, а полный заряд, по теореме
Гаусса, соответствует потоку вектора
напряженности (через поверхность между обкладок
и площадью равной площади обкладок, - вне
идеального плоского конденсатора поле
отсутствует).
Индукция магнитного поля отражает плотность
намотки и силу тока в соленоиде и изображается
густотой линий вектора поля, их количеством на 1м площади. Каждый виток создает
поток вектора напряженности через поверхность
поперечного сечения соленоида. Полное
"действие" всех витков отражается их
суммарным потоком или потокосцеплением: площади. Каждый виток создает
поток вектора напряженности через поверхность
поперечного сечения соленоида. Полное
"действие" всех витков отражается их
суммарным потоком или потокосцеплением: 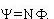
Аналогично электроемкости, индуктивность отражает
способность некоторой обмотки, контура с током
"накапливать" полный поток магнитного поля,
она численно равна потоку, создаваемому в
контуре единицей проходящего по нему тока:
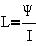
Пример 3. . Найдем индуктивность
соленоида.
Так как площадь всех N витков соленоида
одинакова, поле однородное и перпендикулярно
поперечному сечению, то потокосцепление в
соленоиде длиной l и площадью поперечного
сечения S равно:
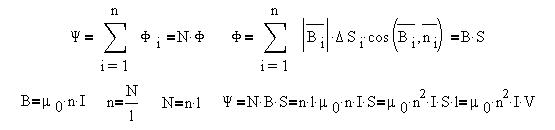
Наконец, индуктивность соленоида равна:
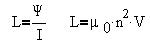
Как видим, индуктивность определяется
габаритами соленоида, а также плотностью
намотки: и при создании поля, и при суммировании
потоков всех витков. Магнетик изменяет
индуктивность в 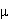 раз.
раз.
Сила Лоренца.
Изменение магнитного состояния физического
вакуума вызывает как реакцию появление
противоположного состояния - электрического
поля, у которого, однако, нет источников в виде
электрических зарядов и которое, следовательно,
является вихревым электрическим полем.
Пусть, например, положительный точечный заряд Q
влетает в однородное магнитное поле B со
скоростью v за плоскость чертежа:
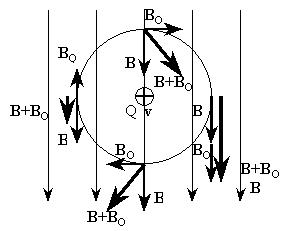
На "мгновенной фотографии" видно, что
силовые линии результирующего магнитного поля ,
векторной суммы B+BQ
однородного поля B поля движущегося заряда BQ, искривились: сгустились справа и
разредились слева от заряда.
Сила, "восстанавливающая" конфигурацию
магнитного поля, прямопропорциональна Q, v
("отвечающих" за поле BQ) и B
(интенсивность "потревоженного" состояния);
направление этой силы "выталкивания" заряда
Q интуитивно ясно из чертежа: справа налево.
Сила, действующая на электрический заряд,
движущийся в магнитном поле, называется силой
Лоренца:
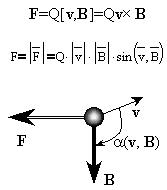
Очевидно, сила Лоренца не производит работу над
движущимся зарядом.
Пример 1. Рассмотрим траекторию
электрона, влетевшего со скоростью 10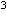 м/с в однородное магнитное поле с
индукцией 10 м/с в однородное магнитное поле с
индукцией 10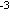 Тл
перпендикулярно силовым линиям: Тл
перпендикулярно силовым линиям:
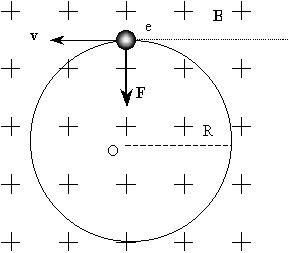
Сила Лоренца оказывается центростремительной
силой:
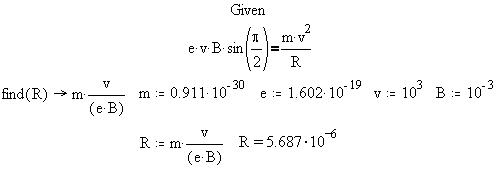
Сила Ампера.
В магнитном поле В сила Лоренца,
действующая на проводник с током, называется
силой Ампера:
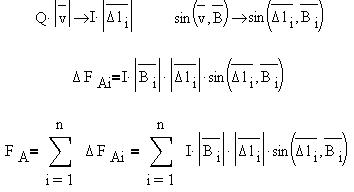
Пример 2. Найдем силу взаимодействия
двух прямых длинных параллельных проводников с
противоположно направленными токами:
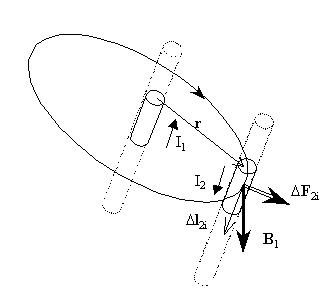
Каждый элемент  l2i тока I2
находится в поле B1 тока I1: l2i тока I2
находится в поле B1 тока I1:
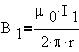
Угол между элементом  l2i и
вектором B1 +90 l2i и
вектором B1 +90 , поэтому сила Ампера, действующая на
элемент тока I2 будет равна: , поэтому сила Ампера, действующая на
элемент тока I2 будет равна:
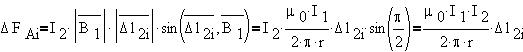
и направлена вдоль r.
Величина, численно равная силе, действующей на
единицу длины проводника с током I2,
оказывается равной:
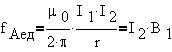
Контур с электрическим током.
Наиболее общей формой проводника с током
является замкутый проводник или контур
(он "состоит" из незамкнутых участков).
В общем случае контур с током пронизывает поток
не только магнитного поля "собственного"
тока, но и внешнего магнитного поля.
Будем считать конфигурацию контура, ориентацию
его в пространстве, силу тока в нем и внешнее
магнитное поле постоянными, стационарными.
Момент сил Ампера.
Рассмотрим прямоугольный контур с протекающим
в нем постоянным током, помещенный в однородное
магнитное поле:
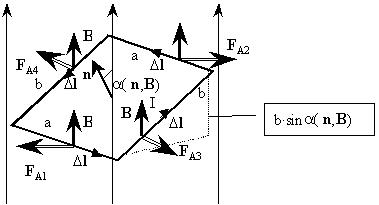
Как видно из рисунка, на контур площадью S=ab
(стороны длиной а перпендикулярны полю)
действуют две двойки горизонтальных
(перпендикулярных полю, направленному
вертикально вверх) сил: силы FA3 и FA4, стремящиеся растянуть (при
противоположном направлении тока - сжать) контур,
деформировать его, и пара сил FA1 и
FA2, создающая вращающий момент,
равный:
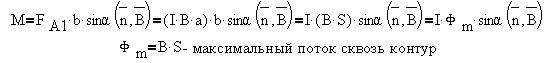
Отсюда ясны способы увеличения вращающего
момента электрического двигателя: увеличение
магнитного поля статора, усиление тока обмотки
ротора, увеличение габаритов ротора,
использование ферромагнетиков.
Работа силы Ампера.
Оценим работу, совершающуюся источником тока в
прямоугольном контуре, помещенном в однородное
магнитное поле (поле перпендикулярно плоскости
контура и направлено за чертеж) при изменении его
размеров под действием сила Ампера (например, при
движении подвижной перемычки):
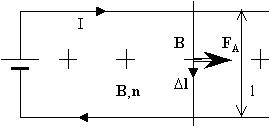
При малом перемещении dx перемычки под
действием силы Ампера совершается элементарная
работа, равная:
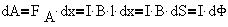
Для конечного перемещения из положения
перемычки 1 в положение 2 работа, соответственно,
равна:
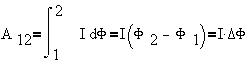
В нашем случае знак работы положительный:
произошло увеличение потока магнитного поля за
счет энергии поддерживающего ток источника (во
внешнем поле изменений не произошло).
Уравнения Максвелла.
Для стационарных, неизменных во
времени электрического поля Е и магнитного
поля В, применив дважды (к каждому полю)
теорему Гаусса и теорему о циркуляции, мы
получили систему уравнений, называемыми уравнениями
Максвелла:
1) поток вектора напряженности электрического
поля Е сквозь замкнутую поверхность
прямопропорционален алгебраической сумме
зарядов, охватываемой этой поверхностью:
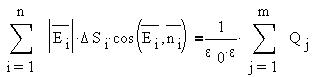
2) циркуляция вектора Е по любому замкнутому
контуру равна нулю:
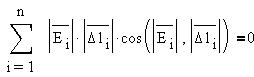
3) поток вектора индукции магнитного поля В
сквозь произвольную замкнутую поверхность равен
нулю:
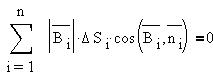
4) циркуляция вектора В по любому замкнутому
контуру прямопропорциональна алгебраической
сумме токов, охватываемых этим контуром:
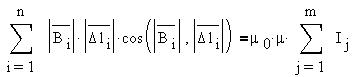
Электрическое и магнитное поля - формы
проявления единого электромагнитного поля:
- магнитное поле, как уже упоминалось, есть особое
состояние физического вакуума, возникающее
прямопропорционально скорости изменения его
электрического состояния; причиной такого
изменения наряду с токами, упорядоченным
движением свободных носителей заряда, могут быть
и открытые Максвеллом токи смещения,
представляющие собой либо просто изменение
во времени потока электрического поля сквозь
охватываемую контуром поверхность, не
связанное с движущимися зарядами, либо
совокупное явление: и изменение электрического
поля, и упорядоченное движение связанных
зарядов диэлектрика при его поляризации в
изменяющемся электрическом поле, при этом в
каждой области пространства магнитное поле
представляет собой правовинтовой вихрь
относительно вектора тока смещения:
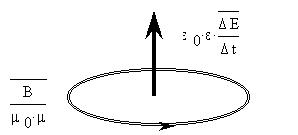
- вихревое электрическое поле возникает
как особое состояние физического вакуума,
прямопропорциональное скорости изменения его
магнитного состояния, при этом электрическое
поле образует левовинтовой вихрь
относительно вектора скорости изменения
магнитного поля:
Внесем изменения во второе и четвертое
уравнения Максвелла:
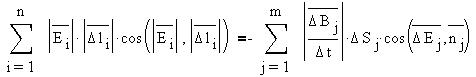
Циркуляция вектора Е по любому замкнутому
контуру равна со знаком минус скорости изменения
магнитного потока через любую замкнутую
поверхность, ограниченную данным контуром. При
этом под Е понимается не только вихревое
электрическое поле, но и электростатическое
(циркуляция которого равна нулю).
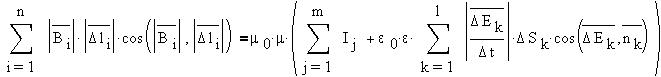
Циркуляция вектора В по любому замкнутому
контуру прямопропорциональна полному току (току
проводимости и току смещения) через произвольную
поверхность, ограниченную данным контуром.
Теперь становится ясным, что электрическое и
магнитное поля как формы электромагнитного поля
испытывают взаимопревращения, не являясь в общем
случае независимыми друг от друга. Более того, из
уравнений Максвелла следует, что
электромагнитное поле способно существовать и
без электрических зарядов и токов - в форме
электромагнитной волны, скорость распостранения
которой в вакууме - электродинамическая
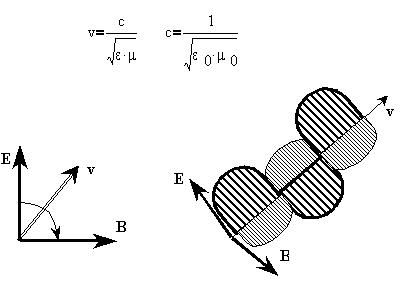
постоянная с. В такой волне векторы Е и В
колеблются "в фазе", образуя правовинтовую
тройку относительно вектора скорости
распостранения волны v, при этом в
непроводящей неферромагнитной среде скорость
равна:
Закон Фарадея.
Закон электромагнитной индукции Фарадея -
основной закон электродинамики,
"венчающий" собой систему ее законов.
Основной закон - это закон
причинно-следственной связи в явлении, когда наиболее
общий объект данной отрасли знаний
испытывает изменение наиболее общего
характера, и следствие определяется
причиной - интенсивностью, скоростью такого
изменения.
Как мы уже выяснили, таким общим объектом
является замкнутый проводник - контур с током,
находящийся во внешнем магнитном поле.
Изменения, очевидно, могут состоять в деформации
контура, в изменении его положения в
пространстве относительно внешнего поля,
изменения силы тока в контуре, наконец - в
изменении самого внешнего поля. Во всех случаях
претерпевает изменение поток магнитного поля
через контур:
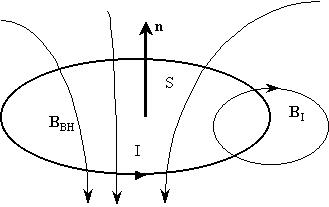
Рассмотрим для простоты по отдельности: 1)
изменение площади контура в однородном
постоянном магнитном поле; 2) изменение внешнего
магнитного поля при неподвижном контуре; 3)
изменение силы тока в неподвижном контуре при
постоянстве внешнего магнитного поля.
1. Изменение площади контура в
однородном постоянном магнитном поле.
Расположим прямоугольный контур с
перемещающейся с постоянной скоростью
перемычкой перпендикулярно силовым линиям
однородного внешнего магнитного поля:
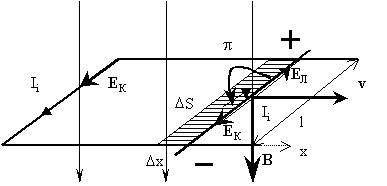
При движении перемычки в магнитном поле
свободные носители заряда перемычки в поле силы
Лоренца EЛ движутся, образуя
индукционный ("наведенный") ток Ii
и приведя к накапливанию избыточного
положительного заряда в точке "+". Далее под
действием кулоновского поля ток идет в контуре
против часовой стрелки. В точке "-" заряды
попадают опять в поле силы Лоренца, которая в
качестве "сторонней" силы совершает работу
против кулоновского поля, поддерживая дисбаланс
избыточных зарядов на концах перемычки.
Считая положительным направлением на
перемычке направление от "+" к "-",
найдем ЭДС индукции, т. е. величину, численно
равную работе силы Лоренца над +1 Кл против
кулоновского поля при перемещении заряда по
перемычке (сопротивлением контура пренебрегаем):
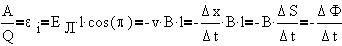
Итак, единственным изменением в состоянии
контура оказалось приращение потока магнитного
поля. Как следствие, возникла сторонняя ЭДС,
прямопропорциональная скорости изменения
потока со знаком "-". Последнее
обстоятельство называется правилом Ленца.
Отрицательный знак ЭДС отражает сопротивление
системы изменению ее состояния. В нашем случае
такое сопротивление имеет и
механический, и электромагнитный характер.
Во-первых, на контур с индукционным током в
магнитном поле действуют силы Ампера, которые
противодействуют перемещению перемычки, так что
для поддержания постоянной скорости ее движения
необходимо приложить компенсирующую силу Ампера
силу тяги:
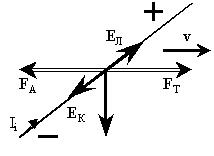
Работа силы Ампера, как было подсчитано ранее,
равна Ii  Ф, работа силы Лоренца, с учетом закона
Фарадея, равна Ф, работа силы Лоренца, с учетом закона
Фарадея, равна 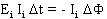 ,
так что полная работа электромагнитного поля
равна нулю, - ведь рассмотренные силы действуют
перпендикулярно скорости зарядов! ЭДС
поддерживается только за счет работы силы тяги: ,
так что полная работа электромагнитного поля
равна нулю, - ведь рассмотренные силы действуют
перпендикулярно скорости зарядов! ЭДС
поддерживается только за счет работы силы тяги: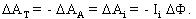
Во-вторых, поток магнитного поля индукционного
тока уменьшает изменение потока внешнего поля:
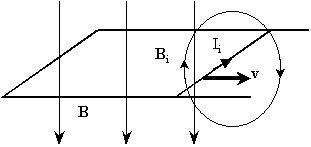
В любом случае, предположив, что правило Ленца
несправедливо, мы получим противоречие с законом
сохранения энергии - вечный двигатель 1-го рода,
дающий бесконечную работу от первичного толчка.
Замечание. Если направить вектор
нормали к плоскости рассмотренного контура
вдоль внешнего поля, то, как уже замечалось,
положительное направление обхода для расчета
циркуляции соотносится с направлением вектора
нормали по правилу правого винта. Сила Лоренца
направлена против положительного направления
обхода (в нашем случае - против часовой стрелки), и
ее циркуляция, численно равная работе над +1 Кл
между точками "-" и "+" (в остальном
контуре поле Лоренца отсутствует) опять же
отрицательна. Здесь и далее - лишь частные случаи
уравнения Максвелла о циркуляции электрического
поля.
2. Изменение внешнего магнитного поля
при неподвижном контуре.
Рассмотрим проводящий контур в форме
окружности, помещенный в нарастающее с
постоянной скоростью внешнее однородное
магнитное поле:
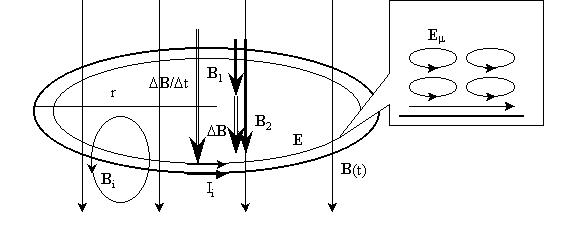
Направим вектор нормали к контуру вдоль
нарастающего поля. Поток внешнего магнитного
поля положителен, положительное направление
обхода - по часовой стрелке.
Прямопропорционально модулю скорости
изменения индукции магнитного поля  B/ B/ t в каждой области
контура образуются электрические вихревые поля E t в каждой области
контура образуются электрические вихревые поля E (см. выноску на чертеже),
компенсирующие друг друга везде в плоскости
контура, кроме ее периферии, вдоль проводника.
Результирующее вихревое поле Е направлено
вдоль проводника против положительного
направления обхода. Величина суммарного
вихревого поля прямопропорциональна количеству
N "периферийных" вихрей, т. е. длине
окружности - ее радиусу, а также интенсивности E (см. выноску на чертеже),
компенсирующие друг друга везде в плоскости
контура, кроме ее периферии, вдоль проводника.
Результирующее вихревое поле Е направлено
вдоль проводника против положительного
направления обхода. Величина суммарного
вихревого поля прямопропорциональна количеству
N "периферийных" вихрей, т. е. длине
окружности - ее радиусу, а также интенсивности E отдельный вихрей, т. е. скорости
изменения магнитного поля. Циркуляция Е
также прямопропорциональна длине окружности, т.
е. ее радиусу. Итого, циркуляция вектора
вихревого электрического поля
прямопропорциональна скорости изменения поля и
квадрату радиуса контура, т. е. его площади, а
значит - скорости изменения потока внешнего
магнитного поля сквозь контур, и записывается со
знаком минус. отдельный вихрей, т. е. скорости
изменения магнитного поля. Циркуляция Е
также прямопропорциональна длине окружности, т.
е. ее радиусу. Итого, циркуляция вектора
вихревого электрического поля
прямопропорциональна скорости изменения поля и
квадрату радиуса контура, т. е. его площади, а
значит - скорости изменения потока внешнего
магнитного поля сквозь контур, и записывается со
знаком минус.
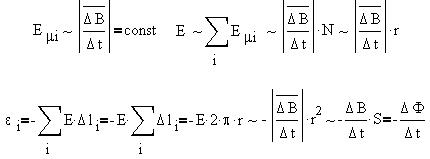
Как видно из чертежа, магнитное поле
индукционного тока уменьшает нарастание потока
внешнего поля.
Замечание. Разрыв проводника контура
привел бы к накоплению на его концах избыточного
заряда и к появлению кулоновского поля,
направленного в положительном направлении
обхода контура, как и в предыдущем случае.
3) Изменение силы тока в неподвижном контуре
при постоянстве внешнего магнитного поля
(самоиндукция).
При изменении силы тока  I в контуре с
индуктивностью L изменение потока магнитного
поля, создаваемого током контура Ф=LI составит I в контуре с
индуктивностью L изменение потока магнитного
поля, создаваемого током контура Ф=LI составит  Ф=L Ф=L I. ЭДС
индукции, называемая в этом случае ЭДС
самоиндукции, будет равна: I. ЭДС
индукции, называемая в этом случае ЭДС
самоиндукции, будет равна:
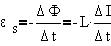
Индукционный ток направлен так, что его
магнитное поле ослабляет любое изменение потока
магнитного поля меняющегося тока контура.
Сохранение магнитного потока.
В общем случае пусть в переменном магнитном
поле произвольным образом движется и
деформируется контур с изменяющимся током. При
этом в контуре индуцируется ток:
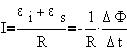
В сверхпроводящем контуре R=0, а поскольку ток I
не может быть бесконечно большим, то 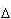 F/ F/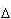 t=0 и F=const, что и
обспечивается индукционными токами согласно
правилу Ленца. t=0 и F=const, что и
обспечивается индукционными токами согласно
правилу Ленца.
Замечание. Здесь уместна аналогия с
сохранением импульса движущейся без трения и
взамодействия с другими телами материальной
точки. Можно продолжить аналогию с механикой и
записать, с учетом 3-го закона Ньютона, что сила
реакции со стороны тела, импульс которого
изменяется, равна:
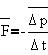
В этой форме основной закон динамики
"похож" на основной закон электродинамики,
закон Фарадея.
Взаимная индукция.
Рассмотрим два близко находящиеся неподвижные
взаимодействующие контуры1 и 2:
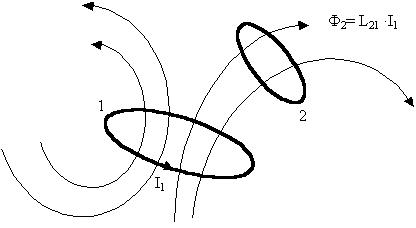
Ток I1 создает в контуре 2 магнитный
поток . Точно так же ток I2 создает в
контуре 1 поток Ф1= L12I2. Коэффициенты пропорциональности
называются взаимными индуктивностями
контуров и численно равны потокам, создаваемым в
одном контуре единицей тока другого контура.
Согласно теореме взаимности, при
отсутствии ферромагнетиков взаимные
индуктивности двух контуров одинаковы: L21=
L12. Иными словами, одинаковый ток в
одном контуре создает одинаковый поток в другом:
Ф1= Ф2.
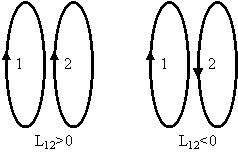
Замечание. Контуры могут
"подмагничивать" друг друга, а могут и
размагничивать в случае противоположной
ориентации токов по отношению к направлению
потока. Взаимная индуктивность, таким образом,
величина алгебраическая (в отличие от
индуктивности, которая всегда положительна):
ЭДС взаимной индукции.
Магнитное взаимодействие контуров проявляется
в том, что всякое изменение тока в одном контуре
вызывает в другом, согласно закону Фарадея, ЭДС
индукции, равную:
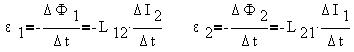
Энергия магнитного поля.
Пусть в контуре с сопротивлением R и ЭДС 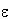 0 за время dt
установился ток I, при этом сторонние силы
источника тока выполнили работу и против ЭДС
самоиндукции (против "противоЭДС"): 0 за время dt
установился ток I, при этом сторонние силы
источника тока выполнили работу и против ЭДС
самоиндукции (против "противоЭДС"):
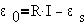
За время dt сторонние силы источника тока
совершили элементарную работу, равную
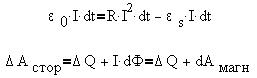
dAмагн - это элементарная работа
против ЭДС самоиндукции в процессе установления
потока Ф магнитного поля, энергия которого W
равна полной работе Aмагн:
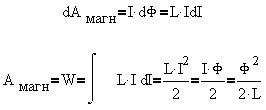
Рассмотрим пример однородного магнитного поля
соленоида:
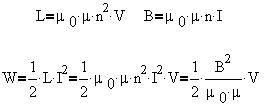
Как видно, энергия магнитного поля
распределена по всему объему, занимаемому полем,
с объемной плотностью энергии, равной:
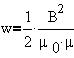
Замечание. В случае ферромагнитной
среды необходимо учесть, что часть dAмагн
идет еще и на нагрев ферромагнетика при его
перемагничивании из-за гистерезисного характера
этого процесса.
Энергия взаимодействия контуров.
При установлении токов во взимодействующих
контурах сторонние силы их ЭДС совершают
дополнительную работу не только против ЭДС
самоиндукции (для установления потока
магнитного поля "собственного" тока),но и
против ЭДС индукции, возникающей в процессе
установления потока магнитного поля,
создаваемого током другого контура.
Энергии магнитного поля, созданного током I2 в контуре 1 и током I1 в
контуре 2 соответственно равны:
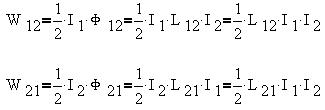
Так как L12=L21, то
энергия магнитного взаимодействия контуров или
их взаимная энергия составит:
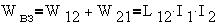
Полная энергия системы из двух
взаимодействующих контуров оказалась равной:
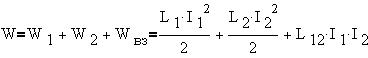
Замечание. Помимо того, что энергия
взаимодействующих контуров оказалась величиной не
аддитивной, заметим, что взаимная энергия
- величина алгебраическая: ее знак определяется
знаком взаимной индуктивности и зависит от
взаимной ориентации токов. Полная энергия
системы, очевидно, величина положительная.
Изложенные в пособии методы и понятия
позволяют изучать основы электротехники и
полупроводниковой электроники, эффективно
используя компьютерную и экспериментальную
поддержку.
Иродов И.Е. Основные законы
электромагнетизма: Учеб. пособие для студентов
вузов.- 2-е, стереотип.- М.: Высш. шк., 1991.- 288 с.: ил.
Содержание
Вернуться на страницу
<Методические разработки> |

