Вернуться
на страницу <Методические разработки>
Содержание
Элементы математического анализа
Рассмотрим графики линейно возрастающей от 0
функции f(x) аргумента x и функции f`(x) - тангенса
угла её наклона к оси x:
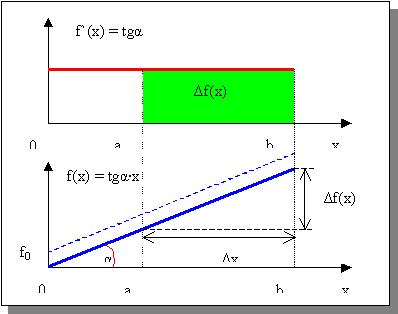
Рис. 1
Будем воспринимать функцию f(x) не как некую
статичную картинку, а наоборот, как закон
изменения ординаты при движении от 0 вправо по
оси x. Здесь ордината равномерно нарастает,
скорость нарастания в любой точке есть отношение
приращения ординаты 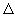 f к приращению аргумента f к приращению аргумента 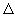 x и равна tg x и равна tg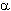 или функции f`(x),
которая как закон скорости изменения функции
f(x) определена ею же и является по отношению к
этой производящей, первичной, образующей, первообразной
- вторичной, образованной, производной. или функции f`(x),
которая как закон скорости изменения функции
f(x) определена ею же и является по отношению к
этой производящей, первичной, образующей, первообразной
- вторичной, образованной, производной.
Возможно ли обратное определение? Да, возможно.
В самом деле, площадь под графиком
производной при движении от 0 вправо по оси x
нарастает как произведение приращения  x на f`(x) и в
нашем случае для любого x просто совпадает с
первообразной: x на f`(x) и в
нашем случае для любого x просто совпадает с
первообразной:

Здесь учтено, что изменение аргумента от 0 до
любого x равно 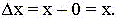
Заметим, что закон изменения функции совпадает
с самой функцией, как в нашем случае, только для
функций, проходящих через 0. На рис. 1
пунктиром проведена функция, пересекающая ось
ординат в точке f0. Её изменение также совпадает с
законом нарастания площади под графиком
производной, но сама она отличается от f(x) на
постоянную величину f0. Но для любой
первообразной, т. е. функции типа f(x) + fo, закон
скорости её изменения будет один и тот же: f`(x).
Площадь под графиком f`(x) при движении по оси
нарастает как некий итог, результат, эффект
движения (как, например, путь под графиком
скорости механического движения), некое целое,
интеграл, причем, поскольку закон нарастания
площади не определяет "в точности" одну
первообразную, а подразумевает множество
отличающихся друг от друга на постоянную
величину первообразных, то он называется неопределённым
интегралом.
Зато изменение всех первообразных 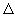 f на
конкретном отрезке изменения аргумента f на
конкретном отрезке изменения аргумента 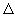 x, например на
отрезке [a, b] (рис. 1), одно и то же и равно: x, например на
отрезке [a, b] (рис. 1), одно и то же и равно:
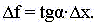
Этому значению соответствует площадь под
графиком производной функции f`(x) между
значениями аргумента x = a и x = b. Такое вполне
определённое число называется определённым
интегралом от функции f`(x). Очевидно, что 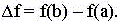
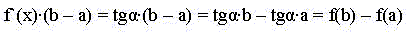
На графике f`(x) (рис. 1) f(b) есть "итог"
нарастания площади под графиком вплоть до x = b, а
f(a) - такой же "итог" вплоть до x = a. Разность
этих "итогов" и есть "оставшаяся"
площадь или определённый интеграл.
В свою очередь, первообразная функция f(x)
есть одновременно и производная для "своей"
первообразной F(x), закон скорости изменения
которой она представляет как на рис. 2:
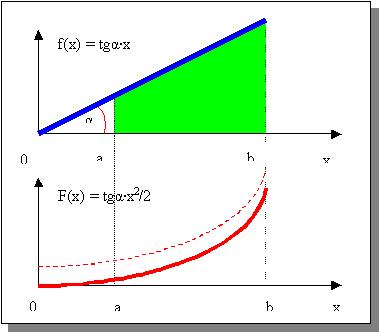
Рис. 2
Площадь под графиком f(x) при движении от 0 вправо
по оси x нарастает как площадь прямоугольного
треугольника:
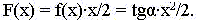
Разумеется, мы нашли лишь одну из бесконечного
множества первообразных, отличающихся между
собой на постоянную, чему на графике
соответствовало бы множество парабол, сдвинутых
друг относительно друга по вертикали (парабола,
изображённая пунктиром на рис. 2). Но
скорость изменения ординат всех таких парабол
описывается одном и тем же законом f(x).
Найдём площадь под графиком f(x) или
определённый интеграл от f(x) на интервале
изменения аргумента x от a до b как площадь
трапеции. Она равна:
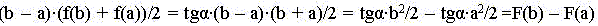
В случае нелинейных функций производится
разбиение области определения функции (оси x) на
последовательность стремящихся к 0 отрезков dx, на
каждом из которых изменение функции 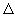 f
приближается к линейному приращению df, так что
понятия, введённые выше, сохраняют, в общем, свой
геометрический и физический смысл. Рассмотрим
пример некоторой функции (рис. 3): f
приближается к линейному приращению df, так что
понятия, введённые выше, сохраняют, в общем, свой
геометрический и физический смысл. Рассмотрим
пример некоторой функции (рис. 3):
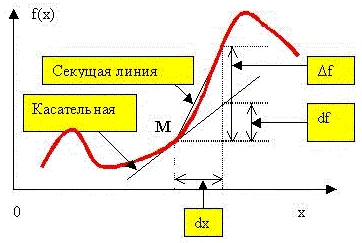
Рис. 3
Здесь, в процессе dx > 0, линейная часть df
приращения функции 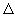 f,
называемая дифференциалом функции f(x) в точке М,
стремится к полному приращению функции f,
называемая дифференциалом функции f(x) в точке М,
стремится к полному приращению функции 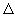 f, так как,
очевидно, при dx > 0, "в точке", секущая и
касательная совпадают так же, как касательная к
линейной функции совпадает с самой функцией (рис.
1, 2). f, так как,
очевидно, при dx > 0, "в точке", секущая и
касательная совпадают так же, как касательная к
линейной функции совпадает с самой функцией (рис.
1, 2).
Замечание 1. Величина, "стремящаяся к
0" в математическом анализе называется
"бесконечно малой величиной" и обозначается
с помощью "знаковой приставки" d.
Замечание 2. Значок неопределённого
интеграла (растянутая по вертикали латинская
буква S) придумал в XVII веке Лейбниц, создавший
одновременно с Ньютоном основы математического
анализа:
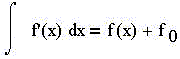
Замечание 3. Значок определённого
интеграла выглядит как
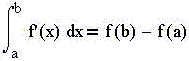
Полностью приведённое выражение носит
название теорема Ньютона - Лейбница и
яляется основной теоремой математического
анализа. Обозначения a и b, соответственно,
называются нижним и верхним пределами
интегрирования.
Двойственную роль функции, изложенную выше,
можно вполне резюмировать цитатой Ньютона (Исаак
Ньютон. Математические начала натуральной
философии (1687 г.)):
"Площадь кривой есть непрестанно
рождающееся количество, увеличивающееся
непрерывной флюксией (производной, - И.Х.),
пропорциональной ординате кривой".
Замечание 4. Уточним терминологию:
1) нахождение закона скорости изменения
функции в любой точке области её определения
называется дифференцированием;
2) нахождение закона нарастания площади под
графиком функции (формулы множества
первообразных для функции как их производной) называется
интегрированием;
3) производная от функции f(x) обозначается f`(x)
(читается: "эф прим от икс равно дэ эф от икс по
дэ икс") :
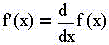
4) неопределённый интеграл от функции f(x) по
переменной x обозначается:
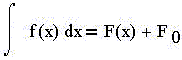
и читается: "неопределённый интеграл от f(x) по
dx"; в правой части выражения - некоторая
первообразная F(x) плюс некоторая (неопределённая,
любая) постоянная величина, константа F0;
5) определённый интеграл от функции f(x) на
отрезке изменения аргумента [a, b] обозначается:
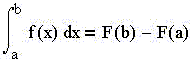
и читается: " определённый интеграл от
функции f(x) от а до b по dx".
Определить закон скорости изменения
функции (формулы тангенса угла наклона
касательной к функции в точке к оси x, закона
"крутизны" функции), т. е. формулу
производной, и закон нарастания площади
под графиком функции (т. е. формулу
неопределённого интеграла) не составляет
особого труда, если перед глазами - график
функции, как это позволяет осуществить MathCAD.
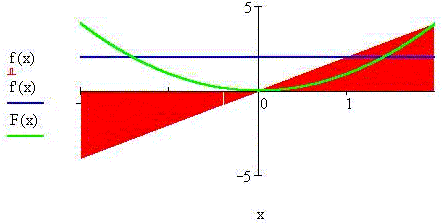
Создадим "тренажёр" в MathCAD 7 Professional,
позволяющий выводить график функции f(x) с
заштрихованной площадью под графиком, график
производной этой функции f`(x) (синего цвета) и график
неопределенного интеграла F(x) (первообразной
с прибавлением константы F0 = 0, - зелёного цвета).
Попробуем дифференцировать и интегрировать
функцию по виду её графика, "на глаз".
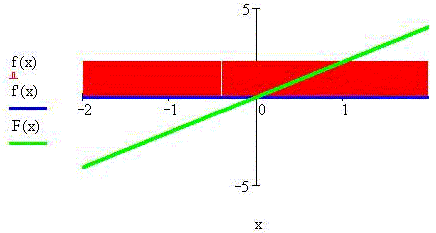
Пример 1. Пусть функция f(x) есть
постоянная величина, равная 2:
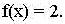
Тогда скорость её изменения, очевидно, нулевая,
а площадь по графиком функции нарастает как 2·x:
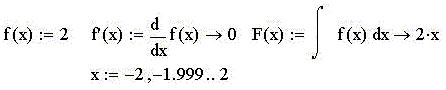
Пример 2. Пусть функция f(x) = 2·x. В этом
случае tg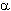 = 2, а
площадь под графиком растёт как 2·x2/2: = 2, а
площадь под графиком растёт как 2·x2/2:
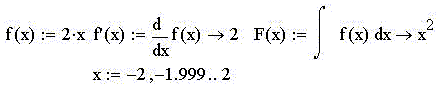
Вообще, очевидно, что "крутизна" степенной
функции xn прямо пропорциональна степени n и,
поскольку тангенс угла наклона касательной к оси
x находится как отношение приращений ординаты и
аргумента и геометрическая размерность
уменьшается на 1, xn/x:
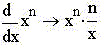
А формула площади под графиком степенной
функции, во-первых, имеет геометрическую
размерность, большую на 1, и, во-вторых, как это
очевидно на интервале изменения аргумента [-1, 1],
обратно пропорциональна показателю степени:
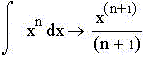
Обе формулы легко проверяются на
вышеприведённых графиках функций f(x) = 2·x0 и f(x) =
2·x1.
Особый интерес представляет дифференцирование
и интегрирование гармонических функций.
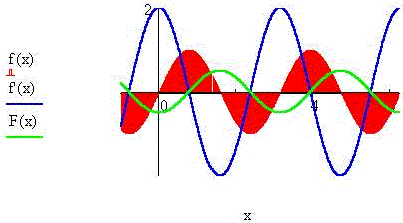
Пример 3. Например, "крутизна"
функции sin(x) за пол-периода меняется от
положительного максимума до отрицательного
минимума, при этом, очевидно, чем больше угловая
частота, тем "круче", "быстрее" меняется
синус x. Площадь под синусоидой пол-периода
возрастает, затем пол-периода падает (за счёт
прибавления "отрицательной" площади), а чем
больше частота, тем "медленнее" нарастает
площадь под графиком. Поскольку, очевидно, и
закон скорости изменения sin(x) и закон нарастания
площади под графиком sin(x) - периодические функции,
то первый суть:
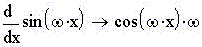
а второй -
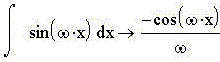
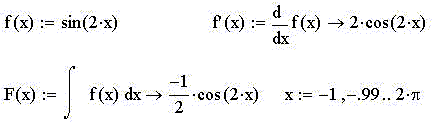
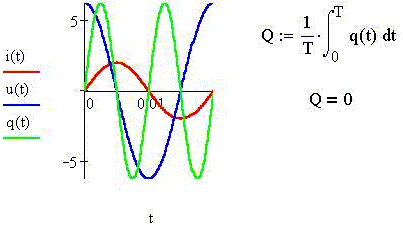
Пример 4. Построим в MathCAD графики
мгновенных значений силы тока, напряжения,
реактивной мощности, а также найдём среднюю за
период реактивную мощность на индуктивном
элементе электрической цепи переменного
синусоидального тока частоты 50 Гц:
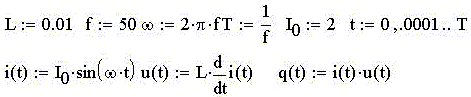
До сих пор мы имели дело с функциями одной
переменной.
В случае n переменных приращение функции f(x1,…,
xn) определяется в равной степени (суммарно) её
приращениями, пропорциональными скорости
изменения функции по каждой из xi переменных, т. е.
частными производными функции по отдельным
переменным. Каждая xi из переменных
"действуют" независимо от остальных,
поэтому и дифференцирование по отдельной
переменной производится "как бы не замечая"
остальных, т. е. считая в момент нахождения
частной производной по xi переменной все прочие
переменные за постоянные.
Геометрически ситуация представляется так, что
"частное дифференцирование" в какой-то
точке производится в плоскости, "параллельной
соответствующей xi переменной", т. е.
параллельно плоскости xi0f(x1,…, xn). Иными словами,
находится формула тангенса угла наклона между
касательной к кривой пересечения плоскости,
параллельной плоскости xi0f(x1,…, xn) и проходящей
через данную точку, и координатной плоскостью.
Сумма произведений частных производных на
приращения соответствующих переменных
называтся полным дифференциалом функции
нескольких переменных.
Для случая двух переменных (3 - мерная функция)
найдем формулы полного дифференциала.
Пример 5. Пусть z(x,y) = x2·sin(2·y). Тогда
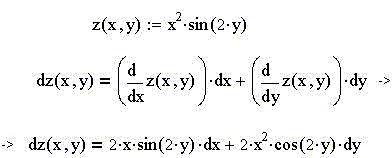
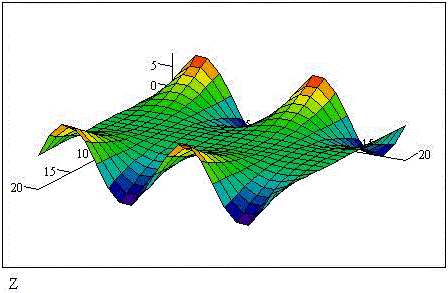
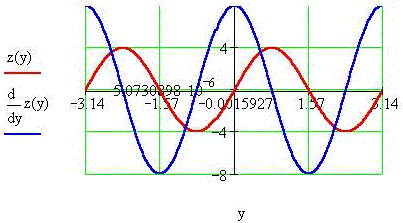
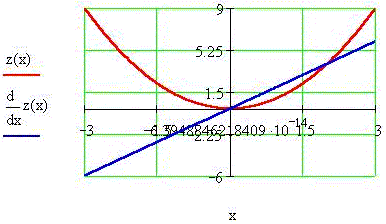
Пример 6. Построим в MathCAD трёхмерную
поверхность такого "параболического
синуса", а также получим плоские сечения и их
производные вдоль плоскостей x0z и y0z в точке x0 = 2 и
y0 =  /4. /4.
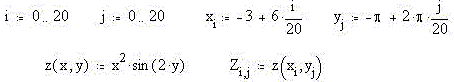
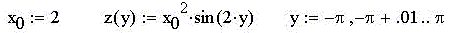
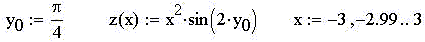
Формула полного дифференциала функции
нескольких переменных необходима при обработке
результатов косвенных измерений - для получения
формул абсолютной и относительной погрешностей
косвенных измерений. При этом в качестве
приращений переменных фигурируют абсолютные
погрешности прямых измерений.
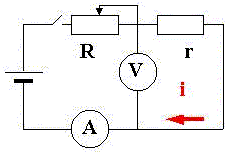
Пример 7. Косвеннное измерение
сопротивления резистора по закону Ома.
Приведём принципиальную схему эксперимента:
1-й этап состоит в получении формулы абсолютной
погрешности и "структурированной" формулы
относительной погрешности:
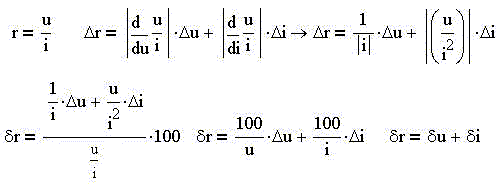
В структуре формулы относительной погрешности
проявился вклад погрешностей прямых измерений в
результирующую погрешность косвенного
измерения, что позволяет заранее планировать
точность и оценивать методику прямых измерений.
2-й этап. Прямые однократные измерения
напряжения u и силы тока i производим школьными
измерительными приборами класса точности 4% с
номинальными значениями, соответственно, 15 В и 2
А. Указанные характеристики приборов используем
для определения абсолютных погрешностей прямых
измерений Du и Di. Абсолютную погрешность
косвенного измерения сопротивления r находим по
формуле полного дифференциала относительно
абсолютных погрешностей прямых измерений.
Для оценки методики эксперимента находим также
конкретную структуру относительной погрешности
косвенного измерения.
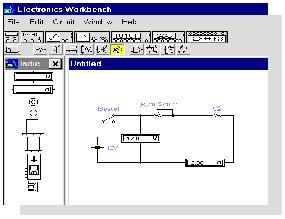
Замечание. В процессе подготовки к
физическому опыту желательно провести
"электронный эксперимент" в Electronics Workbench 4.0:
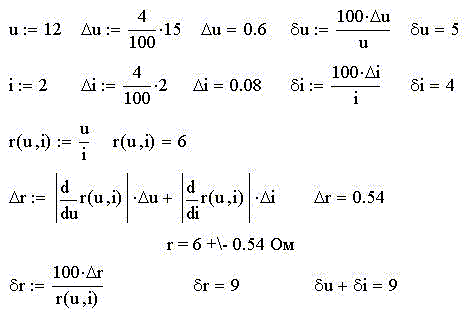
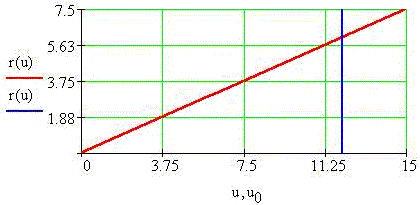
Из вышеизложенного следует, что возможно
несколько повысить точность измерения за счет
увеличения напряжения.
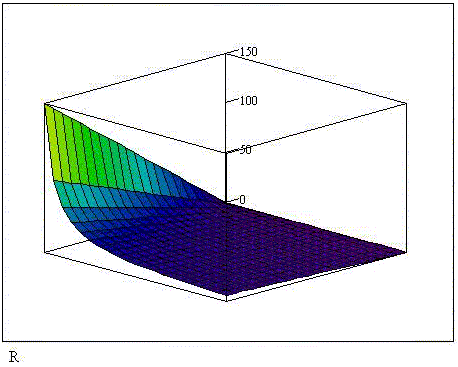
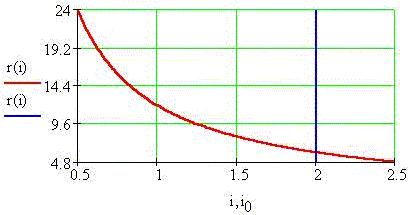
Весьма интересно в MathCAD построить 3-мерную
математическую модель "экспериментального
пространства" и 2-мерные её сечения, как это
сделано ниже:
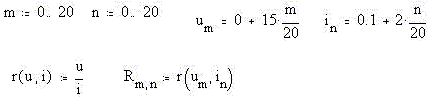
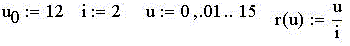
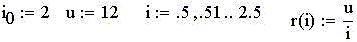
Умение пользоваться аппаратом классического
математического анализа позволяет учащимся
более конкретно исследовать физические явления,
улучшая качество знаний в нескольких разделах
курса физики, а также оказывает существенную
поддержку в последующем образовательном
процессе.
Содержание
Вернуться на страницу
<Методические разработки> |

